Общая теория относительности

Учебник Роберта Уолда для аспирантов см. в разделе «Общая теория относительности» (книга) .

Более доступное и менее техническое введение в эту тему см. в разделе « Введение в общую теорию относительности» .

Продолжительность: 35 секунд. 0:35

черной дыры Компьютерное моделирование замедленного движения двойной системы GW150914, как ее видит ближайший наблюдатель, в течение 0,33 с после ее финального подъема , слияния и звонка . Звездное поле за черными дырами сильно искажается и кажется вращающимся и движущимся из-за сильного гравитационного линзирования , поскольку само пространство-время искажается и увлекается вращающимися черными дырами .

Общая теория относительности , также известная как общая теория относительности и теория гравитации Эйнштейна , представляет собой геометрическую теорию гравитации , опубликованную Альбертом Эйнштейном в 1915 году, и является текущим описанием гравитации в современной физике . Общая теория относительности обобщает специальную теорию относительности и уточняет закон всемирного тяготения Ньютона , обеспечивая единое описание гравитации как геометрического свойства пространства и времени или четырехмерного пространства-времени . В частности, кривизна пространства-времени напрямую связана с энергией и импульсом любой материи и излучения присутствующей . Связь задается уравнениями поля Эйнштейна , системой дифференциальных уравнений в частных производных второго порядка .

Закон всемирного тяготения Ньютона , описывающий классическую гравитацию, можно рассматривать как предсказание общей теории относительности для почти плоской геометрии пространства-времени вокруг стационарных распределений масс. Однако некоторые предсказания общей теории относительности выходят за рамки закона всемирного тяготения Ньютона в классической физике . Эти предсказания касаются течения времени, геометрии пространства, движения тел в свободном падении и распространения света и включают гравитационное замедление времени , гравитационное линзирование , гравитационное красное смещение света, временную задержку Шапиро и сингулярности / черный цвет. отверстия . До сих пор было показано, что все тесты общей теории относительности согласуются с теорией. Зависящие от времени решения общей теории относительности позволяют нам говорить об истории Вселенной и обеспечили современную основу для космологии , что привело к открытию Большого взрыва и космического микроволнового фонового излучения. Несмотря на появление ряда альтернативных теорий Общая теория относительности продолжает оставаться простейшей теорией, согласующейся с экспериментальными данными .

Однако примирение общей теории относительности с законами квантовой физики остается проблемой, поскольку существует отсутствие самосогласованной теории квантовой гравитации . Пока неизвестно, как гравитацию можно объединить с тремя негравитационными силами: сильной , слабой и электромагнитной .

Теория Эйнштейна имеет астрофизические последствия, включая предсказание черных дыр — областей пространства, в которых пространство и время искажены таким образом, что ничто, даже свет , не может покинуть их. Черные дыры — это конечное состояние массивных звезд . Микроквазары и активные ядра галактик считаются звездными черными дырами и сверхмассивными черными дырами . Оно также предсказывает гравитационное линзирование , при котором искривление света приводит к множеству изображений одного и того же отдаленного астрономического явления. Другие предсказания включают существование гравитационных волн , которые наблюдались непосредственно физической коллаборацией LIGO и другими обсерваториями. Кроме того, общая теория относительности послужила основой космологических моделей расширяющейся Вселенной .

Общую теорию относительности, получившую широкое признание как необыкновенную красоту , часто называют самой красивой из всех существующих физических теорий.

История

Основные статьи: История общей теории относительности и классические теории гравитации.

Анри Пуанкаре Теория динамики электрона 1905 года была релятивистской теорией, которую он применил ко всем силам, включая гравитацию. В то время как другие думали, что гравитация мгновенная или имеет электромагнитное происхождение, он предположил, что теория относительности «была следствием наших методов измерения». В своей теории он показал, что гравитационные волны распространяются со скоростью света. Вскоре после этого Эйнштейн начал думать о том, как включить гравитацию в свою релятивистскую теорию. В 1907 году, начав с простого мысленного эксперимента с участием наблюдателя в свободном падении (FFO), он приступил к восьмилетним поискам релятивистской теории гравитации. После многочисленных отклонений и фальстартов его работа завершилась представлением Прусской академии наук в ноябре 1915 года того, что сейчас известно как уравнения поля Эйнштейна, которые составляют ядро ​​общей теории относительности Эйнштейна. Эти уравнения определяют, как на геометрию пространства и времени влияют присутствующие материя и излучение. Версия неевклидовой геометрии , называемая римановой геометрией , позволила Эйнштейну разработать общую теорию относительности, предоставив ключевую математическую основу, на которой он поместил свои физические идеи гравитации. На эту идею указал математик Марсель Гроссман и опубликовали Гроссманн и Эйнштейн в 1913 году.

Уравнения поля Эйнштейна нелинейны и считаются трудными для решения. Эйнштейн использовал методы аппроксимации при разработке первоначальных предсказаний теории. Но в 1916 году астрофизик Карл Шварцшильд нашел первое нетривиальное точное решение уравнений поля Эйнштейна — метрику Шварцшильда . Это решение заложило основу для описания заключительных стадий гравитационного коллапса и объектов, известных сегодня как черные дыры. первые шаги по обобщению решения Шварцшильда на электрически заряженные В том же году были предприняты объекты, что в конечном итоге привело к решению Рейсснера-Нордстрема , которое теперь связано с электрически заряженными черными дырами . В 1917 году Эйнштейн применил свою теорию ко Вселенной в целом, положив начало релятивистской космологии. В соответствии с современным мышлением он предположил, что Вселенная статична, добавив к своим первоначальным уравнениям поля новый параметр — космологическую постоянную — чтобы соответствовать этому наблюдательному предположению. Однако к 1929 году работы Хаббла и других показали, что наша Вселенная расширяется. Это легко описывается расширяющимися космологическими решениями, найденными Фридманом в 1922 году и не требующими космологической постоянной. Лемэтр использовал эти решения для формулирования самой ранней версии модели Большого взрыва , в которой наша Вселенная развилась из чрезвычайно горячего и плотного раннего состояния. Позже Эйнштейн объявил космологическую константу самой большой ошибкой в ​​своей жизни.

В тот период общая теория относительности оставалась чем-то вроде диковинки среди физических теорий. Она явно превосходила ньютоновскую гравитацию , согласовываясь со специальной теорией относительности и объясняя несколько эффектов, необъяснимых теорией Ньютона. Эйнштейн показал в 1915 году, как его теория объясняла аномальное продвижение перигелия планеты Меркурий без каких-либо произвольных параметров (« факторов выдумки »), а в 1919 году экспедиция под руководством Эддингтона подтвердила предсказание общей теории относительности об отклонении звездного света Солнцем во время полного солнечного затмения 29 мая 1919 года . мгновенно сделав Эйнштейна знаменитым. Тем не менее, эта теория оставалась вне основного направления теоретической физики и астрофизики до тех пор, пока не начались ее разработки примерно между 1960 и 1975 годами, которые сейчас известны как золотой век общей теории относительности . Физики начали понимать концепцию черной дыры и идентифицировать квазары как одно из астрофизических проявлений этих объектов. Все более точные испытания Солнечной системы подтвердили предсказательную силу теории. и релятивистская космология также стала поддаваться прямым наблюдательным проверкам.

Общая теория относительности приобрела репутацию теории необыкновенной красоты. Субраманьян Чандрасекхар отметил, что на многих уровнях общая теория относительности демонстрирует то, что Фрэнсис Бэкон назвал «странностью пропорций» ( т. е . элементы, вызывающие изумление и удивление). Он сопоставляет фундаментальные концепции (пространство и время в сравнении с материей и движением), которые ранее считались совершенно независимыми. Чандрасекхар также отметил, что единственными ориентирами Эйнштейна в поисках точной теории были принцип эквивалентности и его ощущение того, что правильное описание гравитации должно быть геометрическим в своей основе, так что в том, как это происходит, существовал «элемент откровения». Эйнштейн пришел к своей теории. Другими элементами красоты, связанными с общей теорией относительности, являются ее простота и симметрия, способ, которым она включает в себя инвариантность и унификацию, а также ее идеальная логическая последовательность.

В предисловии к книге «Относительность: специальная и общая теория » Эйнштейн сказал: «Настоящая книга призвана, насколько это возможно, дать точное представление о теории относительности тем читателям, которые с общенаучной и философской точки зрения интересуются теорией, но не знакомы с математическим аппаратом теоретической физики. Работа предполагает уровень образования, соответствующий уровню вступительного экзамена в университет, и, несмотря на краткость книги, изрядный объем. терпение и сила воли со стороны читателя. Автор не пожалел усилий, стремясь изложить основные идеи в наиболее простой и доходчивой форме и в целом в той последовательности и связи, в которой они действительно возникли. ."

От классической механики к общей теории относительности

Общую теорию относительности можно понять, исследуя ее сходства с классической физикой и отличия от нее. Первым шагом является осознание того, что классическая механика и закон гравитации Ньютона допускают геометрическое описание. Сочетание этого описания с законами специальной теории относительности приводит к эвристическому выводу общей теории относительности.

Геометрия ньютоновской гравитации

Согласно общей теории относительности, объекты в гравитационном поле ведут себя аналогично объектам в ускоряющемся пространстве. Например, наблюдатель увидит падение шара в ракете (слева) так же, как и на Земле (справа), при условии, что ускорение ракеты равно 9,8 м/с. ² (ускорение силы тяжести на поверхности Земли).

В основе классической механики лежит представление о том, что движение тела можно описать как комбинацию свободного (или инерционного ) движения и отклонений от этого свободного движения. Такие отклонения вызваны внешними силами, действующими на тело в соответствии со вторым законом движения Ньютона , который гласит, что результирующая сила, действующая на тело, равна (инерционной) массе этого тела, умноженной на его ускорение . Предпочтительные инерционные движения связаны с геометрией пространства и времени: в стандартных системах отсчета классической механики объекты, находящиеся в свободном движении, движутся по прямым линиям с постоянной скоростью. Говоря современным языком, их пути — это геодезические , прямые мировые линии в искривленном пространстве-времени.

И наоборот, можно было бы ожидать, что инерционные движения, идентифицированные путем наблюдения за реальными движениями тел и учета внешних сил (таких как электромагнетизм или трение ), могут быть использованы для определения геометрии пространства, а также координаты времени . Однако, когда в игру вступает гравитация, возникает двусмысленность. Согласно закону гравитации Ньютона и независимо подтвержденному экспериментами, такими как эксперимент Этвёша и его последователей (см. Эксперимент Этвёша ), существует универсальность свободного падения (также известная как принцип слабой эквивалентности или универсальное равенство инерционного и пассивного движения). -гравитационная масса): траектория пробного тела в свободном падении зависит только от его положения и начальной скорости, но не от каких-либо свойств его материала. Упрощенная версия этого воплощена в эксперименте Эйнштейна с лифтом , показанном на рисунке справа: для наблюдателя, находящегося в закрытой комнате, невозможно решить, отображая траекторию тел, таких как брошенный мяч, является ли комната неподвижно в гравитационном поле и ускоряющемся шаре или в свободном пространстве на борту ракеты, ускоряющейся со скоростью, равной скорости гравитационного поля, по отношению к шару, который после выпуска имеет нулевое ускорение.

Учитывая универсальность свободного падения, не существует заметного различия между движением по инерции и движением под действием силы гравитации. Это предполагает определение нового класса движения по инерции, а именно класса объектов, находящихся в свободном падении под действием силы тяжести. Этот новый класс предпочтительных движений также определяет геометрию пространства и времени — в математических терминах это геодезическое движение, связанное с определенной связью , которая зависит от градиента гравитационного потенциала . Пространство в этой конструкции все еще имеет обычную евклидову геометрию . Однако пространство- время в целом сложнее. Как можно показать с помощью простых мысленных экспериментов, прослеживающих траектории свободного падения различных пробных частиц, результат транспортировки векторов пространства-времени, которые могут обозначать скорость частицы (времяподобные векторы), будет меняться в зависимости от траектории частицы; математически говоря, ньютоновская связь неинтегрируема . Отсюда можно сделать вывод, что пространство-время искривлено. В результате Теория Ньютона-Картана представляет собой геометрическую формулировку ньютоновской гравитации с использованием только ковариантных концепций, то есть описания, которое справедливо в любой желаемой системе координат. В этом геометрическом описании приливные эффекты — относительное ускорение тел в свободном падении — связаны с производной связи, показывая, как измененная геометрия вызвана наличием массы.

Релятивистское обобщение

Световой конус

Какой бы интригующей ни была геометрическая ньютоновская гравитация, ее основа, классическая механика, представляет собой всего лишь предельный случай (специальной) релятивистской механики. На языке симметрии : там, где гравитацией можно пренебречь, физика является лоренц-инвариантной, как в специальной теории относительности, а не инвариантом Галилея, как в классической механике. (Определяющей симметрией специальной теории относительности является группа Пуанкаре , которая включает перемещения, вращения, ускорения и отражения.) Различия между ними становятся существенными, когда мы имеем дело со скоростями, приближающимися к скорости света , и с явлениями высоких энергий.

Благодаря лоренцевой симметрии в игру вступают дополнительные структуры. Они определяются набором световых конусов (см. изображение). Световые конусы определяют причинную структуру: для каждого события A существует набор событий, которые в принципе могут либо влиять, либо подвергаться влиянию A посредством сигналов или взаимодействий, которым не обязательно двигаться быстрее света (например, событие Б на изображении), а также набор событий, для которых такое влияние невозможно (например, событие С на изображении). Эти множества не зависят от наблюдателя . В сочетании с мировыми линиями свободно падающих частиц световые конусы можно использовать для восстановления полуримановой метрики пространства-времени, по крайней мере, с точностью до положительного скалярного коэффициента. В математических терминах это определяет конформную структуру или конформная геометрия.

Специальная теория относительности определяется отсутствием гравитации. Для практических приложений это подходящая модель, когда гравитацией можно пренебречь. Принимая во внимание гравитацию и предполагая универсальность движения свободного падения, применимо рассуждение, аналогичное предыдущему разделу: не существует глобальных инерциальных систем отсчета . Вместо этого существуют приблизительные инерциальные системы отсчета, движущиеся рядом со свободно падающими частицами. В переводе на язык пространства-времени: прямые времяподобные линии, определяющие невесомую инерциальную систему отсчета, деформируются в линии, изогнутые относительно друг друга, что позволяет предположить, что включение гравитации требует изменения геометрии пространства-времени.

Априори неясно, совпадают ли новые локальные системы отсчёта в свободном падении с системами отсчёта, в которых действуют законы специальной теории относительности — эта теория основана на распространении света и, следовательно, на электромагнетизме, который мог бы иметь другой набор предпочтительных кадров . Но, используя разные предположения относительно специальных релятивистских систем отсчета (например, о том, что они закреплены на Земле или находятся в свободном падении), можно сделать разные предсказания относительно гравитационного красного смещения, то есть того, как частота света смещается по мере изменения светового потока. распространяется через гравитационное поле (см. ниже ). Фактические измерения показывают, что в свободно падающих системах свет распространяется так же, как в специальной теории относительности. Обобщение этого утверждения, а именно, что законы специальной теории относительности соблюдают хорошее приближение в свободно падающих (и невращающихся) системах отсчета, известно как принцип эквивалентности Эйнштейна , важнейший руководящий принцип для обобщения специальной релятивистской физики, включая гравитацию. .

Те же экспериментальные данные показывают, что время, измеряемое часами в гравитационном поле — собственное время , если выражаться техническим термином, — не подчиняется правилам специальной теории относительности. На языке геометрии пространства-времени оно не измеряется метрикой Минковского . Как и в случае Ньютона, это наводит на мысль о более общей геометрии. В малых масштабах все системы отсчета, находящиеся в свободном падении, эквивалентны и примерно соответствуют системе Минковского. Следовательно, мы сейчас имеем дело с искривленным обобщением пространства Минковского. Метрический тензор , определяющий геометрию (в частности, то, как измеряются длины и углы), не является метрикой Минковского специальной теории относительности, это обобщение, известное как полу- или псевдориманова метрика. Более того, каждой римановой метрике естественно сопоставляется один конкретный вид связи — связность Леви-Чивита , и это, по сути, связь, которая удовлетворяет принципу эквивалентности и делает пространство локально Минковским (т. е. в подходящих локально инерциальные координаты , метрика Минковского, а ее первые частные производные и коэффициенты связи обращаются в нуль).

Уравнения Эйнштейна

Основные статьи: уравнения поля Эйнштейна и математика общей теории относительности.

Сформулировав релятивистскую, геометрическую версию эффектов гравитации, остается вопрос об источнике гравитации. В ньютоновской гравитации источником является масса. В специальной теории относительности масса оказывается частью более общей величины, называемой тензором энергии-импульса , которая включает в себя как энергии и импульса, плотность так и напряжение : давление и сдвиг. Используя принцип эквивалентности, этот тензор легко обобщается на искривленное пространство-время. Продолжая далее аналогию с геометрической ньютоновской гравитацией, естественно предположить, что уравнение поля гравитации связывает этот тензор и тензор Риччи , который описывает особый класс приливных эффектов: изменение объема небольшого облака пробных частиц, которое вначале покоятся, а затем свободно падают. В специальной теории относительности сохранение энергии -импульса соответствует утверждению о том, что тензор энергии-импульса не имеет дивергенций . Эту формулу также легко обобщить на искривленное пространство-время, заменив частные производные их аналогами для искривленного многообразия , ковариантными производными, изучаемыми в дифференциальной геометрии. При этом дополнительном условии — ковариантная дивергенция тензора энергии-импульса и, следовательно, всего, что находится на другой стороне уравнения, равна нулю — простейшим нетривиальным набором уравнений являются так называемые уравнения Эйнштейна (поля):

Уравнения поля Эйнштейна

$G_{\mu \nu }\equiv R_{\mu \nu }-{\textstyle 1 \over 2}R\,g_{\mu \nu }=\kappa T_{\mu \nu }\,$

В левой части находится тензор Эйнштейна , $G_{\mu \nu }$, который является симметричным и представляет собой определенную бездивергентную комбинацию тензора Риччи $R_{\mu \nu }$ и метрика. В частности,

$R=g^{\mu \nu }R_{\mu \nu }$

— скаляр кривизны. Сам тензор Риччи связан с более общим тензором кривизны Римана следующим образом:

$R_{\mu \nu }={R^{\alpha }}_{\mu \alpha \nu }.$

С правой стороны, $\kappa$ является константой и $T_{\mu \nu }$ – тензор энергии-импульса. Все тензоры записаны в абстрактной индексной нотации . Сопоставление предсказаний теории с результатами наблюдений за планет орбитами или, что то же самое, обеспечение того, что пределом слабой гравитации и низкой скорости является механика Ньютона, константа пропорциональности $\kappa$ оказывается ${\textstyle \kappa ={\frac {8\pi G}{c^{4}}}}$, где $G$ – ньютоновская постоянная гравитации и $c$ скорость света в вакууме. Когда материи нет и тензор энергии-импульса обращается в нуль, результатом являются вакуумные уравнения Эйнштейна:

$R_{\mu \nu }=0.$

В общей теории относительности мировая линия частицы, свободной от всех внешних, негравитационных сил, представляет собой особый тип геодезической в ​​искривленном пространстве-времени. Другими словами, свободно движущаяся или падающая частица всегда движется по геодезической.

Геодезическое уравнение :

${d^{2}x^{\mu } \over ds^{2}}+\Gamma ^{\mu }{}_{\alpha \beta }{dx^{\alpha } \over ds}{dx^{\beta } \over ds}=0,$

где $s$ — скалярный параметр движения (например, собственное время ), а $\Gamma ^{\mu }{}_{\alpha \beta }$ являются символами Кристоффеля (иногда называемыми коэффициентами аффинной связности или коэффициентами связности Леви-Чивита ), которые симметричны по двум нижним индексам. Греческие индексы могут принимать значения: 0, 1, 2, 3, а соглашение о суммировании. для повторяющихся индексов используется $\alpha$ и $\beta$. Величина в левой части этого уравнения представляет собой ускорение частицы, и поэтому это уравнение аналогично законам движения Ньютона , которые также дают формулы для ускорения частицы. В этом уравнении движения используются обозначения Эйнштейна , что означает, что повторяющиеся индексы суммируются (т.е. от нуля до трех). Символы Кристоффеля являются функциями четырех координат пространства-времени и поэтому не зависят от скорости или ускорения или других характеристик пробной частицы , движение которой описывается уравнением геодезических.

Полная сила в общей теории относительности

Смотрите также: Задача двух тел в общей теории относительности.

В общей теории относительности эффективная гравитационная потенциальная энергия объекта массы m, вращающегося вокруг массивного центрального тела M, определяется выражением

$U_{f}(r)=-{\frac {GMm}{r}}+{\frac {L^{2}}{2mr^{2}}}-{\frac {GML^{2}}{mc^{2}r^{3}}}$

Тогда консервативную полную силу можно получить как ее отрицательный градиент.

$F_{f}(r)=-{\frac {GMm}{r^{2}}}+{\frac {L^{2}}{mr^{3}}}-{\frac {3GML^{2}}{mc^{2}r^{4}}}$

где L — угловой момент . Первый член представляет собой силу ньютоновской гравитации , которая описывается законом обратных квадратов. Второй член представляет собой центробежную силу при круговом движении. Третий член представляет собой релятивистский эффект.

Альтернативы общей теории относительности

Основная статья: Альтернативы общей теории относительности

Существуют альтернативы общей теории относительности, основанные на тех же предпосылках, которые включают дополнительные правила и/или ограничения, ведущие к другим уравнениям поля. Примерами являются теория Уайтхеда , теория Бранса-Дикке , телепараллелизм , f ( R )-гравитация и теория Эйнштейна-Картана .

Определение и основные приложения

Смотрите также: Математика общей теории относительности и физические теории, модифицированные общей теорией относительности.

Вывод, описанный в предыдущем разделе, содержит всю информацию, необходимую для определения общей теории относительности, описания ее ключевых свойств и решения вопроса решающей важности в физике, а именно, как эту теорию можно использовать для построения моделей.

Определение и основные свойства

Общая теория относительности — это метрическая теория гравитации. В его основе лежат уравнения Эйнштейна , которые описывают связь между геометрией четырехмерного псевдориманова многообразия, представляющего пространство-время, и энергией-импульсом, содержащейся в этом пространстве-времени. Явления, которые в классической механике приписываются действию силы гравитации (такие как свободное падение , орбитальное движение и космического корабля траектории ), соответствуют инерционному движению в искривленной геометрии пространства-времени в общей теории относительности; нет гравитационной силы, отклоняющей объекты от их естественных прямых траекторий. Вместо этого гравитация соответствует изменениям свойств пространства и времени, что, в свою очередь, меняет самые прямые пути, по которым объекты будут естественным образом следовать. Искривление, в свою очередь, вызвано энергией-импульсом материи. Перефразируя релятивиста Джона Арчибальда Уиллера , пространство-время указывает материи, как двигаться; материя сообщает пространству-времени, как искривляться.

Хотя общая теория относительности заменяет скалярный гравитационный потенциал классической физики симметричным ранга второго тензором сводится к первому , последний в некоторых предельных случаях . Для слабых гравитационных полей и малой скорости относительно скорости света предсказания теории сходятся с предсказаниями закона всемирного тяготения Ньютона.

Поскольку общая теория относительности построена с использованием тензоров, она демонстрирует общую ковариацию : ее законы – и последующие законы, сформулированные в рамках общей релятивистской структуры – принимают одну и ту же форму во всех системах координат . Более того, теория не содержит никаких инвариантных геометрических фоновых структур, т.е. она не зависит от фона . Таким образом, оно удовлетворяет более строгому общему принципу относительности , а именно, что законы физики одинаковы для всех наблюдателей. Локально , как это выражено в принципе эквивалентности, пространство-время является Минковским , а законы физики демонстрируют локальную лоренц-инвариантность .

Моделирование

Основная концепция построения общерелятивистской модели — это решение уравнений Эйнштейна . Учитывая как уравнения Эйнштейна, так и подходящие уравнения для свойств материи, такое решение состоит из конкретного полуриманова многообразия (обычно определяемого путем задания метрики в определенных координатах) и конкретных полей материи, определенных на этом многообразии. Материя и геометрия должны удовлетворять уравнениям Эйнштейна, поэтому, в частности, тензор энергии-импульса материи должен быть бездивергентным. Разумеется, материя также должна удовлетворять любым дополнительным уравнениям, налагаемым на ее свойства. Короче говоря, такое решение — это модель Вселенной, которая удовлетворяет законам общей теории относительности и, возможно, дополнительным законам, управляющим любой присутствующей материей.

Уравнения Эйнштейна представляют собой нелинейные уравнения в частных производных, и поэтому их трудно точно решить. ряд точных решений , хотя лишь немногие из них имеют прямое физическое применение. Тем не менее известен Наиболее известными точными решениями, а также наиболее интересными с точки зрения физики являются решение Шварцшильда , решение Рейсснера-Нордстрема и метрика Керра , каждое из которых соответствует определенному типу черной дыры в пустой Вселенной. и вселенные Фридмана-Леметра-Робертсона-Уокера и де Ситтера , каждая из которых описывает расширяющийся космос. Точные решения, представляющие большой теоретический интерес, включают вселенную Гёделя (которая открывает интригующую возможность путешествий во времени в искривленном пространстве-времени), решение Тауба-НУТ (модель Вселенной, которая является однородной , но анизотропной ) и пространство анти-де Ситтера (которое недавно приобрела известность в контексте так называемой гипотезы Малдасены ).

Учитывая сложность поиска точных решений, уравнения поля Эйнштейна также часто решаются путем численного интегрирования на компьютере или путем рассмотрения небольших возмущений точных решений. В области численной относительности мощные компьютеры используются для моделирования геометрии пространства-времени и решения уравнений Эйнштейна для интересных ситуаций, таких как две сталкивающиеся черные дыры. В принципе, такие методы могут быть применены к любой системе при наличии достаточных компьютерных ресурсов и могут решать фундаментальные вопросы, такие как голые сингулярности . Приблизительные решения также могут быть найдены с помощью теорий возмущений, таких как линеаризованная гравитация. и его обобщение, постньютоновское расширение , оба из которых были разработаны Эйнштейном. Последний обеспечивает систематический подход к решению геометрии пространства-времени, которое содержит распределение материи, движущейся медленно по сравнению со скоростью света. Расширение включает в себя ряд условий; первые члены представляют собой ньютоновскую гравитацию, тогда как более поздние члены представляют собой еще меньшие поправки к теории Ньютона, обусловленные общей теорией относительности. Расширением этого расширения является параметризованный постньютоновский (ППН) формализм, который позволяет количественно сравнивать предсказания общей теории относительности и альтернативных теорий.

Последствия теории Эйнштейна

Общая теория относительности имеет ряд физических последствий. Некоторые следуют непосредственно из аксиом теории, тогда как другие стали ясны только в ходе многих лет исследований, последовавших за первой публикацией Эйнштейна.

Гравитационное замедление времени и сдвиг частоты

Основная статья: Гравитационное замедление времени

Схематическое изображение гравитационного красного смещения световой волны, выходящей с поверхности массивного тела.

Предполагая, что справедлив принцип эквивалентности, гравитация влияет на течение времени. Свет, направленный вниз в гравитационный колодец , имеет синее смещение , тогда как свет, посланный в противоположном направлении (т. е. поднимающийся из гравитационного колодца), смещается в красную сторону ; вместе эти два эффекта известны как гравитационный сдвиг частоты. В более общем плане процессы вблизи массивного тела протекают медленнее по сравнению с процессами, происходящими дальше; этот эффект известен как гравитационное замедление времени.

Гравитационное красное смещение измерено в лаборатории и с помощью астрономических наблюдений. Гравитационное замедление времени в гравитационном поле Земли неоднократно измерялось с помощью атомных часов . в то время как постоянная проверка обеспечивается как побочный эффект работы системы глобального позиционирования (GPS). Тесты в более сильных гравитационных полях обеспечиваются наблюдением двойных пульсаров . Все результаты согласуются с общей теорией относительности. Однако на нынешнем уровне точности эти наблюдения не позволяют отличить общую теорию относительности от других теорий, в которых действует принцип эквивалентности.

Отклонение света и гравитационная задержка времени

Основные статьи: геодезические Шварцшильда , проблема Кеплера в общей теории относительности , гравитационная линза и задержка Шапиро.

Отклонение света (исходящего из места, показанного синим цветом) вблизи компактного тела (показано серым цветом)

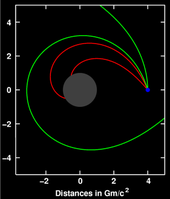
Общая теория относительности предсказывает, что путь света будет повторять кривизну пространства-времени, когда он проходит вблизи звезды. Первоначально этот эффект был подтвержден путем наблюдения за отклонением света звезд или далеких квазаров при прохождении мимо Солнца .

Это и связанные с ним предсказания следуют из того факта, что свет следует так называемой светоподобной или нулевой геодезической — обобщению прямых линий, по которым распространяется свет в классической физике. Такие геодезические являются обобщением инвариантности скорости света в специальной теории относительности. Когда исследуются подходящие модельные пространства-времени (либо внешнее решение Шварцшильда, либо, для более чем одной массы, постньютоновское расширение), выявляется несколько эффектов гравитации на распространение света. Хотя искривление света можно также получить, распространив на свет универсальность свободного падения, угол отклонения, полученный в результате таких расчетов, составляет лишь половину значения, определяемого общей теорией относительности.

С отклонением света тесно связана временная задержка Шапиро — явление, при котором световым сигналам требуется больше времени, чтобы пройти через гравитационное поле, чем в отсутствие этого поля. Было проведено множество успешных проверок этого предсказания. В параметризованном постньютоновском формализме (ППН) измерения как отклонения света, так и гравитационной задержки времени определяют параметр под названием γ, который кодирует влияние гравитации на геометрию пространства.

Гравитационные волны

Основная статья: Гравитационная волна

Кольцо пробных частиц, деформированное проходящей (линеаризованной, усиленной для лучшей видимости) гравитационной волной

Предсказано в 1916 году. Альберт Эйнштейн, существуют гравитационные волны: рябь в метрике пространства-времени, распространяющаяся со скоростью света. Это одна из нескольких аналогий между гравитацией слабого поля и электромагнетизмом в том смысле, что они аналогичны электромагнитным волнам . 11 февраля 2016 года команда Advanced LIGO объявила, что они напрямую обнаружили гравитационные волны от пары черных дыр сливающихся .

Простейший тип такой волны можно представить, воздействуя на кольцо свободно плавающих частиц. Синусоидальная волна, распространяющаяся через такое кольцо в сторону читателя, искажает кольцо характерным ритмичным образом (анимированное изображение справа). Поскольку уравнения Эйнштейна нелинейны , сколь угодно сильные гравитационные волны не подчиняются линейной суперпозиции , что затрудняет их описание. Однако линейные аппроксимации гравитационных волн достаточно точны, чтобы описать чрезвычайно слабые волны, которые, как ожидается, прибудут сюда, на Землю, в результате далеких космических событий, которые обычно приводят к увеличению и уменьшению относительных расстояний на величину $10^{-21}$ или меньше. Методы анализа данных обычно используют тот факт, что эти линеаризованные волны можно разложить по Фурье .

Некоторые точные решения описывают гравитационные волны без какого-либо приближения, например, волновой поезд, движущийся через пустое пространство. или вселенные Гауди , разновидности расширяющегося космоса, наполненного гравитационными волнами. Но для гравитационных волн, возникающих в астрофизически важных ситуациях, таких как слияние двух черных дыр, численные методы в настоящее время являются единственным способом построения соответствующих моделей.

Орбитальные эффекты и относительность направления

Основная статья: Задача двух тел в общей теории относительности

Общая теория относительности отличается от классической механики рядом предсказаний, касающихся вращающихся тел. Он предсказывает общее вращение ( прецессию ) планетарных орбит, а также распад орбит, вызванный излучением гравитационных волн и эффектами, связанными с относительностью направления.

Прецессия апсид

Ньютоновская (красная) и эйнштейновская орбита (синяя) одинокой планеты, вращающейся вокруг звезды. Влияние других планет игнорируется.

Основная статья: Апсидальная прецессия

В общей теории относительности апсиды любой орбиты (точка наибольшего приближения вращающегося тела к центру масс системы ) будут прецессировать ; орбита не является эллипсом , а похожа на эллипс, который вращается в фокусе, в результате чего получается форма, напоминающая розовую кривую (см. изображение). Эйнштейн впервые получил этот результат, используя приблизительную метрику, представляющую предел Ньютона, и рассматривая вращающееся тело как пробную частицу . Для него тот факт, что его теория дала прямое объяснение аномальному сдвигу перигелия Меркурия, обнаруженному ранее Урбеном Леверье в 1859 году, был важным свидетельством того, что он наконец определил правильную форму уравнений гравитационного поля.

Эффект также можно получить, используя либо точную метрику Шварцшильда (описывающую пространство-время вокруг сферической массы), либо точную метрику Шварцшильда (описывающую пространство-время вокруг сферической массы). или гораздо более общий постньютоновский формализм . Это связано с влиянием гравитации на геометрию пространства и вкладом собственной энергии в гравитацию тела (закодированным в нелинейности уравнений Эйнштейна). Релятивистская прецессия наблюдалась для всех планет, на которых можно точно измерить прецессию (Меркурий, Венера и Земля). а также в двойных системах пульсаров, где она больше на пять порядков .

В общей теории относительности сдвиг перигелия $\sigma$, выраженное в радианах на оборот, приблизительно определяется выражением

$\sigma ={\frac {24\pi ^{3}L^{2}}{T^{2}c^{2}(1-e^{2})}}\ ,$

где:

• $L$ полуось большая
• $T$ это орбитальный период
• $c$ это скорость света в вакууме
• $e$ это эксцентриситет орбиты

Орбитальный распад

Орбитальный распад PSR J0737-3039: временной сдвиг (в с ), отслеживаемый за 16 лет (2021 г.).

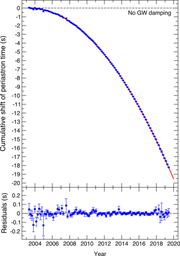
Согласно общей теории относительности, двойная система будет излучать гравитационные волны, теряя при этом энергию. Из-за этой потери расстояние между двумя вращающимися телами уменьшается, как и период их обращения. В пределах Солнечной системы или для обычных двойных звезд эффект слишком мал, чтобы его можно было наблюдать. Это не относится к тесному бинарному пульсару, системе двух орбитальных нейтронных звезд , одна из которых является пульсаром : от пульсара наблюдатели на Земле получают регулярную серию радиоимпульсов, которые могут служить высокоточными часами, которые позволяет точно измерить орбитальный период. Поскольку нейтронные звезды чрезвычайно компактны, значительное количество энергии излучается в виде гравитационного излучения.

Первое наблюдение уменьшения орбитального периода из-за излучения гравитационных волн было сделано Халсом и Тейлором двойного пульсара PSR1913+16 с использованием открытого ими в 1974 году . Это было первое обнаружение гравитационных волн, хотя и косвенное, для которого они были удостоены Нобелевской премии по физике 1993 года. С тех пор было обнаружено несколько других двойных пульсаров, в частности двойной пульсар PSR J0737−3039 , где обе звезды являются пульсарами. и последний раз сообщалось, что она также согласуется с общей теорией относительности в 2021 году после 16 лет наблюдений.

Геодезическая прецессия и перетаскивание системы координат

Основные статьи: Геодезическая прецессия и перетаскивание рамки.

Некоторые релятивистские эффекты напрямую связаны с относительностью направления. Одним из них является геодезическая прецессия : направление оси гироскопа, находящегося в свободном падении в искривленном пространстве-времени, будет меняться по сравнению, например, с направлением света, получаемого от далеких звезд, даже несмотря на то, что такой гироскоп представляет собой способ поддержания столь же стабильного направления, как и возможен (« параллельный транспорт »). Для системы Луна-Земля этот эффект измерен с помощью лунной лазерной локации . Совсем недавно он был измерен для тестовых масс на борту спутника Gravity Probe B с точностью лучше 0,3%.

Вблизи вращающейся массы возникают гравитомагнитные эффекты или волочения рамки эффекты . Удаленный наблюдатель определит, что объекты, близкие к массе, «тащатся». Это наиболее экстремально для вращающихся черных дыр , где для любого объекта, попадающего в зону, известную как эргосфера , вращение неизбежно. Подобные эффекты снова можно проверить на примере их влияния на ориентацию гироскопов в свободном падении. были проведены несколько противоречивые испытания С использованием спутников LAGEOS , подтвердившие релятивистское предсказание. Также Mars Global Surveyor вокруг Марса. использовался зонд

Астрофизические приложения

Гравитационное линзирование

Основная статья: Гравитационное линзирование

Крест Эйнштейна : четыре изображения одного и того же астрономического объекта, полученные гравитационной линзой.

Отклонение света под действием силы тяжести ответственно за новый класс астрономических явлений. Если между астрономом и удаленным целевым объектом с соответствующей массой и относительным расстоянием находится массивный объект, астроном увидит несколько искаженных изображений цели. Такие эффекты известны как гравитационное линзирование. В зависимости от конфигурации, масштаба и распределения массы могут быть два или более изображений: яркое кольцо, известное как кольцо Эйнштейна , или частичные кольца, называемые дугами. Самый ранний пример был обнаружен в 1979 году; с тех пор было обнаружено более сотни гравитационных линз. Даже если несколько изображений расположены слишком близко друг к другу, чтобы их можно было разрешить, эффект все равно можно измерить, например, как общее осветление целевого объекта; ряд таких « событий микролинзирования ». наблюдался

Гравитационное линзирование превратилось в инструмент наблюдательной астрономии . Он используется для обнаружения присутствия и распределения темной материи , предоставления «естественного телескопа» для наблюдения далеких галактик и получения независимой оценки постоянной Хаббла . Статистическая оценка данных линзирования дает ценную информацию о структурной эволюции галактик .

Гравитационно-волновая астрономия

Основные статьи: Гравитационно-волновая и гравитационно-волновая астрономия

Впечатление художника от космического детектора гравитационных волн LISA

Наблюдения за двойными пульсарами предоставляют убедительные косвенные доказательства существования гравитационных волн (см. Орбитальный распад выше). Обнаружение этих волн является основной целью современных исследований, связанных с теорией относительности. несколько наземных детекторов гравитационных волн В настоящее время работают , в первую очередь интерферометрические детекторы GEO 600 , LIGO (два детектора), TAMA 300 и VIRGO . Различные системы синхронизации пульсаров используют миллисекундные пульсары для обнаружения гравитационных волн в 10-ти диапазонах. ⁻⁹ до 10 ⁻⁶ герцовый диапазон частот, которые происходят из двойных сверхмассивных черных дыр. Европейский космический детектор eLISA/NGO в настоящее время находится в стадии разработки. с миссией-предшественником ( LISA Pathfinder ), запущенной в декабре 2015 года.

Наблюдения гравитационных волн обещают дополнить наблюдения в электромагнитном спектре . Ожидается, что они дадут информацию о черных дырах и других плотных объектах, таких как нейтронные звезды и белые карлики, об определенных типах взрывов сверхновых и о процессах в очень ранней Вселенной, включая признаки определенных типов гипотетических космических струн . В феврале 2016 года команда Advanced LIGO объявила, что они обнаружили гравитационные волны от слияния черных дыр.

Черные дыры и другие компактные объекты

Основная статья: Черная дыра

Моделирование на основе уравнений общей теории относительности: коллапс звезды с образованием черной дыры с испусканием гравитационных волн

Всякий раз, когда отношение массы объекта к его радиусу становится достаточно большим, общая теория относительности предсказывает образование черной дыры — области пространства, из которой ничто, даже свет, не может выйти. В принятых в настоящее время моделях звездной эволюции нейтронные звезды с массой около 1,4 солнечных и звездные черные дыры с массами от нескольких до нескольких десятков солнечных считаются конечным состоянием эволюции массивных звезд. Обычно галактика имеет одну сверхмассивную черную дыру с массой от нескольких миллионов до нескольких миллиардов солнечных масс в центре. Считается, что его присутствие сыграло важную роль в формировании галактики и более крупных космических структур.

С астрономической точки зрения наиболее важным свойством компактных объектов является то, что они обеспечивают чрезвычайно эффективный механизм преобразования гравитационной энергии в электромагнитное излучение. Считается, что аккреция , падение пыли или газообразного вещества на звездные или сверхмассивные черные дыры, ответственна за возникновение некоторых поразительно ярких астрономических объектов, особенно разнообразных видов активных галактических ядер галактических масштабов и объектов звездного размера, таких как микроквазары. В частности, аккреция может привести к образованию релятивистских струй — сфокусированных пучков высокоэнергетических частиц, которые выбрасываются в космос почти со скоростью света. Общая теория относительности играет центральную роль в моделировании всех этих явлений. и наблюдения предоставляют убедительные доказательства существования черных дыр со свойствами, предсказанными теорией.

Черные дыры также являются востребованными целями в поисках гравитационных волн (см. Гравитационные волны выше). Слияние двойных черных дыр должно привести к тому, что некоторые из самых сильных сигналов гравитационных волн достигнут детекторов здесь, на Земле, а фазу непосредственно перед слиянием («чип») можно использовать как « стандартную свечу » для определения расстояния до событий слияния. и, следовательно, служат зондом космического расширения на больших расстояниях. Гравитационные волны, возникающие при падении звездной черной дыры в сверхмассивную, должны предоставить прямую информацию о геометрии сверхмассивной черной дыры.

Космология

Основная статья: Физическая космология

Эта синяя подкова — далекая галактика, увеличенная и искривленная в почти полное кольцо под действием сильного гравитационного притяжения массивной светящейся красной галактики на переднем плане.

Современные модели космологии основаны на уравнениях поля Эйнштейна , которые включают космологическую постоянную $\Lambda$ поскольку он оказывает важное влияние на крупномасштабную динамику космоса,

$R_{\mu \nu }-{\textstyle 1 \over 2}R\,g_{\mu \nu }+\Lambda \ g_{\mu \nu }={\frac {8\pi G}{c^{4}}}\,T_{\mu \nu }$

где $g_{\mu \nu }$ является метрикой пространства-времени. Изотропные и однородные решения этих расширенных уравнений, решения Фридмана – Леметра – Робертсона – Уокера , позволят физикам смоделировать Вселенную, которая развивалась за последние 14 миллиардов лет из горячей ранней фазы Большого взрыва. Как только небольшое количество параметров (например, средняя плотность материи во Вселенной) будет зафиксировано астрономическими наблюдениями, дополнительные данные наблюдений могут быть использованы для проверки моделей. Прогнозы, все успешные, включают первоначальное содержание химических элементов, образовавшихся в период первичного нуклеосинтеза . крупномасштабное строение Вселенной, а также существование и свойства « теплового эха» раннего космоса, космического фонового излучения .

Астрономические наблюдения за скоростью космологического расширения позволяют оценить общее количество материи во Вселенной, хотя природа этой материи остается отчасти загадочной. Около 90% всей материи представляет собой темную материю, которая имеет массу (или, что то же самое, гравитационное влияние), но не взаимодействует электромагнитно и, следовательно, не может наблюдаться напрямую. В рамках известной физики элементарных частиц не существует общепринятого описания этого нового вида материи. или иначе. Данные наблюдений, полученные в ходе исследований красных смещений далеких сверхновых, и измерений космического фонового излучения также показывают, что на эволюцию нашей Вселенной существенное влияние оказывает космологическая постоянная, приводящая к ускорению космического расширения, или, что то же самое, форма энергии с необычным уравнением. состояния , известного как темная энергия , природа которой остается неясной.

Инфляционная фаза , дополнительная фаза сильно ускоренного расширения в космические времена около 10 ⁻³³ секунд, была выдвинута гипотеза в 1980 году, объясняющая несколько загадочных наблюдений, которые не были объяснены классическими космологическими моделями, таких как почти идеальная однородность космического фонового излучения. Недавние измерения космического фонового излучения привели к появлению первых доказательств этого сценария. Однако существует ошеломляющее разнообразие возможных инфляционных сценариев, которое невозможно ограничить текущими наблюдениями. Еще более серьезный вопрос — это физика самой ранней Вселенной, существовавшей до фазы инфляции и близкой к тому моменту, когда классические модели предсказывают сингулярность Большого взрыва . Авторитетный ответ потребовал бы полной теории квантовой гравитации, которая еще не разработана. (см. раздел о квантовой гравитации ниже).

Экзотические решения: путешествия во времени, варп-двигатели

Курт Гёдель показал что существуют решения уравнений Эйнштейна, которые содержат замкнутые времяподобные кривые (CTC), которые допускают петли во времени. Решения требуют экстремальных физических условий, которые вряд ли когда-либо возникнут на практике, и остается открытым вопрос, устранят ли их полностью дальнейшие законы физики. С тех пор были найдены другие — столь же непрактичные — решения GR, содержащие ЦОК, такие как цилиндр Типлера и проходимые червоточины . Стивен Хокинг выдвинул гипотезу о защите хронологии , которая представляет собой предположение, выходящее за рамки стандартной общей теории относительности и предотвращающее путешествия во времени .

Некоторые точные решения в общей теории относительности, такие как двигатель Алькубьерре, представляют собой примеры варп-двигателя, но эти решения требуют экзотического распределения материи и обычно страдают от квазиклассической нестабильности.

Расширенные концепции

Асимптотические симметрии

Основная статья: группа Бонди-Мецнера-Сакса

Группа симметрии пространства-времени для специальной теории относительности — это группа Пуанкаре , которая представляет собой десятимерную группу из трех усилений Лоренца, трех вращений и четырех сдвигов пространства-времени. Логично задаться вопросом, какие симметрии, если таковые имеются, могут применяться в общей теории относительности. Разрешимым случаем могло бы стать рассмотрение симметрии пространства-времени, как ее видят наблюдатели, находящиеся вдали от всех источников гравитационного поля. Наивное ожидание асимптотически плоского пространства-времени может заключаться в простом расширении и воспроизведении симметрии плоского пространства-времени специальной теории относительности, а именно. , группа Пуанкаре.

В 1962 году Герман Бонди , М.Г. ван дер Бург, А.В. Мецнер. и Райнер К. Сакс обратился к этой проблеме асимптотической симметрии , чтобы исследовать поток энергии на бесконечности, вызванный распространяющимися гравитационными волнами . Их первым шагом было принятие решения о некоторых физически разумных граничных условиях, которые следует разместить в гравитационном поле на светоподобной бесконечности, чтобы охарактеризовать то, что означает сказать, что метрика асимптотически плоская, не делая априорных предположений о природе асимптотической группы симметрии - даже не предположение, что такая группа существует. Затем, после разработки того, что они считали наиболее разумными граничными условиями, они исследовали природу полученных в результате преобразований асимптотической симметрии, которые оставляют инвариантной форму граничных условий, подходящую для асимптотически плоских гравитационных полей. Они обнаружили, что преобразования асимптотической симметрии действительно образуют группу, и структура этой группы не зависит от конкретного гравитационного поля, которое случайно присутствует. Это означает, что, как и ожидалось, можно отделить кинематику пространства-времени от динамики гравитационного поля по крайней мере на пространственной бесконечности. Загадочным сюрпризом в 1962 году стало открытие богатой бесконечномерной группы (так называемой группы БМС) в качестве асимптотической группы симметрии вместо конечномерной группы Пуанкаре, которая является подгруппой группы БМС. Преобразования Лоренца не только являются преобразованиями асимптотической симметрии, но существуют также дополнительные преобразования, которые не являются преобразованиями Лоренца, но являются преобразованиями асимптотической симметрии. Фактически, они обнаружили дополнительную бесконечность генераторов преобразований, известных как суперпереводы . Отсюда следует вывод, что общая теория относительности (ОТО) не сводится к специальной теории относительности в случае слабых полей на больших расстояниях. Оказывается, что симметрия БМС, соответствующим образом модифицированная, может рассматриваться как переформулировка универсальной теоремы о мягком гравитоне в квантовой теории поля (КТП), которая связывает универсальную инфракрасную (мягкую) КТП с асимптотическими пространственно-временными симметриями ОТО.

Causal structure and global geometry

Main article: Causal structure

Penrose–Carter diagram of an infinite Minkowski universe

In general relativity, no material body can catch up with or overtake a light pulse. No influence from an event A can reach any other location X before light sent out at A to X. In consequence, an exploration of all light worldlines (null geodesics) yields key information about the spacetime's causal structure. This structure can be displayed using Penrose–Carter diagrams in which infinitely large regions of space and infinite time intervals are shrunk ("compactified") so as to fit onto a finite map, while light still travels along diagonals as in standard spacetime diagrams.

Aware of the importance of causal structure, Roger Penrose and others developed what is known as global geometry. In global geometry, the object of study is not one particular solution (or family of solutions) to Einstein's equations. Rather, relations that hold true for all geodesics, such as the Raychaudhuri equation, and additional non-specific assumptions about the nature of matter (usually in the form of energy conditions) are used to derive general results.

Horizons

Main articles: Horizon (general relativity), No hair theorem, and Black hole mechanics

Using global geometry, some spacetimes can be shown to contain boundaries called horizons, which demarcate one region from the rest of spacetime. The best-known examples are black holes: if mass is compressed into a sufficiently compact region of space (as specified in the hoop conjecture, the relevant length scale is the Schwarzschild radius), no light from inside can escape to the outside. Since no object can overtake a light pulse, all interior matter is imprisoned as well. Passage from the exterior to the interior is still possible, showing that the boundary, the black hole's horizon, is not a physical barrier.

The ergosphere of a rotating black hole, which plays a key role when it comes to extracting energy from such a black hole

Early studies of black holes relied on explicit solutions of Einstein's equations, notably the spherically symmetric Schwarzschild solution (used to describe a static black hole) and the axisymmetric Kerr solution (used to describe a rotating, stationary black hole, and introducing interesting features such as the ergosphere). Using global geometry, later studies have revealed more general properties of black holes. With time they become rather simple objects characterized by eleven parameters specifying: electric charge, mass–energy, linear momentum, angular momentum, and location at a specified time. This is stated by the black hole uniqueness theorem: "black holes have no hair", that is, no distinguishing marks like the hairstyles of humans. Irrespective of the complexity of a gravitating object collapsing to form a black hole, the object that results (having emitted gravitational waves) is very simple.

Even more remarkably, there is a general set of laws known as black hole mechanics, which is analogous to the laws of thermodynamics. For instance, by the second law of black hole mechanics, the area of the event horizon of a general black hole will never decrease with time, analogous to the entropy of a thermodynamic system. This limits the energy that can be extracted by classical means from a rotating black hole (e.g. by the Penrose process). There is strong evidence that the laws of black hole mechanics are, in fact, a subset of the laws of thermodynamics, and that the black hole area is proportional to its entropy. This leads to a modification of the original laws of black hole mechanics: for instance, as the second law of black hole mechanics becomes part of the second law of thermodynamics, it is possible for the black hole area to decrease as long as other processes ensure that entropy increases overall. As thermodynamical objects with nonzero temperature, black holes should emit thermal radiation. Semiclassical calculations indicate that indeed they do, with the surface gravity playing the role of temperature in Planck's law. This radiation is known as Hawking radiation (cf. the quantum theory section, below).

There are many other types of horizons. In an expanding universe, an observer may find that some regions of the past cannot be observed ("particle horizon"), and some regions of the future cannot be influenced (event horizon). Even in flat Minkowski space, when described by an accelerated observer (Rindler space), there will be horizons associated with a semiclassical radiation known as Unruh radiation.

Singularities

Main article: Spacetime singularity

Another general feature of general relativity is the appearance of spacetime boundaries known as singularities. Spacetime can be explored by following up on timelike and lightlike geodesics—all possible ways that light and particles in free fall can travel. But some solutions of Einstein's equations have "ragged edges"—regions known as spacetime singularities, where the paths of light and falling particles come to an abrupt end, and geometry becomes ill-defined. In the more interesting cases, these are "curvature singularities", where geometrical quantities characterizing spacetime curvature, such as the Ricci scalar, take on infinite values. Well-known examples of spacetimes with future singularities—where worldlines end—are the Schwarzschild solution, which describes a singularity inside an eternal static black hole, or the Kerr solution with its ring-shaped singularity inside an eternal rotating black hole. The Friedmann–Lemaître–Robertson–Walker solutions and other spacetimes describing universes have past singularities on which worldlines begin, namely Big Bang singularities, and some have future singularities (Big Crunch) as well.

Given that these examples are all highly symmetric—and thus simplified—it is tempting to conclude that the occurrence of singularities is an artifact of idealization. The famous singularity theorems, proved using the methods of global geometry, say otherwise: singularities are a generic feature of general relativity, and unavoidable once the collapse of an object with realistic matter properties has proceeded beyond a certain stage and also at the beginning of a wide class of expanding universes. However, the theorems say little about the properties of singularities, and much of current research is devoted to characterizing these entities' generic structure (hypothesized e.g. by the BKL conjecture). The cosmic censorship hypothesis states that all realistic future singularities (no perfect symmetries, matter with realistic properties) are safely hidden away behind a horizon, and thus invisible to all distant observers. While no formal proof yet exists, numerical simulations offer supporting evidence of its validity.

Evolution equations

Main article: Initial value formulation (general relativity)

Each solution of Einstein's equation encompasses the whole history of a universe—it is not just some snapshot of how things are, but a whole, possibly matter-filled, spacetime. It describes the state of matter and geometry everywhere and at every moment in that particular universe. Due to its general covariance, Einstein's theory is not sufficient by itself to determine the time evolution of the metric tensor. It must be combined with a coordinate condition, which is analogous to gauge fixing in other field theories.

To understand Einstein's equations as partial differential equations, it is helpful to formulate them in a way that describes the evolution of the universe over time. This is done in "3+1" formulations, where spacetime is split into three space dimensions and one time dimension. The best-known example is the ADM formalism. These decompositions show that the spacetime evolution equations of general relativity are well-behaved: solutions always exist, and are uniquely defined, once suitable initial conditions have been specified. Such formulations of Einstein's field equations are the basis of numerical relativity.

Global and quasi-local quantities

Main article: Mass in general relativity

The notion of evolution equations is intimately tied in with another aspect of general relativistic physics. In Einstein's theory, it turns out to be impossible to find a general definition for a seemingly simple property such as a system's total mass (or energy). The main reason is that the gravitational field—like any physical field—must be ascribed a certain energy, but that it proves to be fundamentally impossible to localize that energy.

Nevertheless, there are possibilities to define a system's total mass, either using a hypothetical "infinitely distant observer" (ADM mass) or suitable symmetries (Komar mass). If one excludes from the system's total mass the energy being carried away to infinity by gravitational waves, the result is the Bondi mass at null infinity. Just as in classical physics, it can be shown that these masses are positive. Corresponding global definitions exist for momentum and angular momentum. There have also been a number of attempts to define quasi-local quantities, such as the mass of an isolated system formulated using only quantities defined within a finite region of space containing that system. The hope is to obtain a quantity useful for general statements about isolated systems, such as a more precise formulation of the hoop conjecture.

Relationship with quantum theory

If general relativity were considered to be one of the two pillars of modern physics, then quantum theory, the basis of understanding matter from elementary particles to solid-state physics, would be the other. However, how to reconcile quantum theory with general relativity is still an open question.

Quantum field theory in curved spacetime

Main article: Quantum field theory in curved spacetime

Ordinary quantum field theories, which form the basis of modern elementary particle physics, are defined in flat Minkowski space, which is an excellent approximation when it comes to describing the behavior of microscopic particles in weak gravitational fields like those found on Earth. In order to describe situations in which gravity is strong enough to influence (quantum) matter, yet not strong enough to require quantization itself, physicists have formulated quantum field theories in curved spacetime. These theories rely on general relativity to describe a curved background spacetime, and define a generalized quantum field theory to describe the behavior of quantum matter within that spacetime. Using this formalism, it can be shown that black holes emit a blackbody spectrum of particles known as Hawking radiation leading to the possibility that they evaporate over time. As briefly mentioned above, this radiation plays an important role for the thermodynamics of black holes.

Quantum gravity

Main article: Quantum gravity

See also: String theory, Canonical general relativity, Loop quantum gravity, Causal dynamical triangulation, and Causal sets

Projection of a Calabi–Yau manifold, one of the ways of compactifying the extra dimensions posited by string theory

The demand for consistency between a quantum description of matter and a geometric description of spacetime, as well as the appearance of singularities (where curvature length scales become microscopic), indicate the need for a full theory of quantum gravity: for an adequate description of the interior of black holes, and of the very early universe, a theory is required in which gravity and the associated geometry of spacetime are described in the language of quantum physics. Despite major efforts, no complete and consistent theory of quantum gravity is currently known, even though a number of promising candidates exist.

Attempts to generalize ordinary quantum field theories, used in elementary particle physics to describe fundamental interactions, so as to include gravity have led to serious problems. Some have argued that at low energies, this approach proves successful, in that it results in an acceptable effective (quantum) field theory of gravity. At very high energies, however, the perturbative results are badly divergent and lead to models devoid of predictive power ("perturbative non-renormalizability").

Simple spin network of the type used in loop quantum gravity

One attempt to overcome these limitations is string theory, a quantum theory not of point particles, but of minute one-dimensional extended objects. The theory promises to be a unified description of all particles and interactions, including gravity; the price to pay is unusual features such as six extra dimensions of space in addition to the usual three. In what is called the second superstring revolution, it was conjectured that both string theory and a unification of general relativity and supersymmetry known as supergravity form part of a hypothesized eleven-dimensional model known as M-theory, which would constitute a uniquely defined and consistent theory of quantum gravity.

Another approach starts with the canonical quantization procedures of quantum theory. Using the initial-value-formulation of general relativity (cf. evolution equations above), the result is the Wheeler–deWitt equation (an analogue of the Schrödinger equation) which, regrettably, turns out to be ill-defined without a proper ultraviolet (lattice) cutoff. However, with the introduction of what are now known as Ashtekar variables, this leads to a promising model known as loop quantum gravity. Space is represented by a web-like structure called a spin network, evolving over time in discrete steps.

Depending on which features of general relativity and quantum theory are accepted unchanged, and on what level changes are introduced, there are numerous other attempts to arrive at a viable theory of quantum gravity, some examples being the lattice theory of gravity based on the Feynman Path Integral approach and Regge calculus, dynamical triangulations, causal sets, twistor models or the path integral based models of quantum cosmology.

Observation of gravitational waves from binary black hole merger GW150914

All candidate theories still have major formal and conceptual problems to overcome. They also face the common problem that, as yet, there is no way to put quantum gravity predictions to experimental tests (and thus to decide between the candidates where their predictions vary), although there is hope for this to change as future data from cosmological observations and particle physics experiments becomes available.

Current status

General relativity has emerged as a highly successful model of gravitation and cosmology, which has so far passed many unambiguous observational and experimental tests. However, there are strong indications that the theory is incomplete. The problem of quantum gravity and the question of the reality of spacetime singularities remain open. Observational data that is taken as evidence for dark energy and dark matter could indicate the need for new physics.

Even taken as is, general relativity is rich with possibilities for further exploration. Mathematical relativists seek to understand the nature of singularities and the fundamental properties of Einstein's equations, while numerical relativists run increasingly powerful computer simulations (such as those describing merging black holes). In February 2016, it was announced that the existence of gravitational waves was directly detected by the Advanced LIGO team on 14 September 2015. A century after its introduction, general relativity remains a highly active area of research.

See also

• Alcubierre drive – Hypothetical FTL transportation by warping space (warp drive)
• Alternatives to general relativity – Proposed theories of gravity
• Contributors to general relativity
• Derivations of the Lorentz transformations
• Ehrenfest paradox – Paradox in special relativity
• Einstein–Hilbert action – Concept in general relativity
• Einstein's thought experiments – Albert Einstein's hypothetical situations to argue scientific points
• General relativity priority dispute – Debate about credit for general relativity
• Introduction to the mathematics of general relativity – non-technical introduction to the mathematics of general relativityPages displaying wikidata descriptions as a fallback
• Nordström's theory of gravitation – Predecessor to the theory of relativity
• Ricci calculus – Tensor index notation for tensor-based calculations
• Timeline of gravitational physics and relativity

Библиография

• Альфер, РА ; Герман, Р.К. (1948), «Эволюция Вселенной», Nature , 162 (4124): 774–775, Бибкод : 1948Natur.162..774A , doi : 10.1038/162774b0 , S2CID   4113488
• Андерсон, доктор медицинских наук; Кэмпбелл, Дж. К.; Юргенс, РФ; Лау, Э.Л. (1992), «Последние разработки в области испытаний общей теории относительности на Солнечной системе», Сато, Х.; Накамура, Т. (ред.), Труды шестого совещания Марселя Гроссмана по общей теории относительности , World Scientific, стр. 353–355, ISBN  978-981-02-0950-6
• Арнольд, VI (1989), Математические методы классической механики , Springer, ISBN  978-3-540-96890-0
• Арновитт, Ричард ; Дезер, Стэнли ; Миснер, Чарльз В. (1962), «Динамика общей теории относительности», в Виттене, Луи (редактор), Гравитация: введение в текущие исследования , Уайли, стр. 227–265.
• Арун, КГ; Бланше, Л.; Айер, БР; Кусайла, MSS (2008), «Вдохновляющие компактные двойные системы на квазиэллиптических орбитах: полный поток энергии 3PN», Physical Review D , 77 (6): 064035, arXiv : 0711.0302 , Bibcode : 2008PhRvD..77f4035A , doi : 10.1103/ ФизРевД.77.064035 , S2CID   55825202
• Эшби, Нил (2002), «Относительность и глобальная система позиционирования» (PDF) , Physics Today , 55 (5): 41–47, Бибкод : 2002PhT....55e..41A , doi : 10.1063/1.1485583
• Эшби, Нил (2003), «Относительность в системе глобального позиционирования», Living Reviews in Relativity , 6 (1): 1, Bibcode : 2003LRR.....6....1A , doi : 10.12942/lrr-2003 -1 , ПМК   5253894 , ПМИД   28163638
• Аштекар, Абхай (1986), «Новые переменные для классической и квантовой гравитации», Phys. Преподобный Летт. , 57 (18): 2244–2247, Bibcode : 1986PhRvL..57.2244A , doi : 10.1103/PhysRevLett.57.2244 , PMID   10033673
• Аштекар, Абхай (1987), «Новая гамильтонова формулировка общей теории относительности», Phys. Rev. , D36 (6): 1587–1602, Bibcode : 1987PhRvD..36.1587A , doi : 10.1103/PhysRevD.36.1587 , PMID   9958340
• Аштекар, Абхай (2007), «Петлевая квантовая гравитация: четыре последних достижения и дюжина часто задаваемых вопросов», Одиннадцатая встреча Марселя Гроссмана - о последних разработках в теоретической и экспериментальной общей теории относительности, гравитации и релятивистских теориях поля - Материалы встречи MG11 по общей теории относительности : 126, arXiv : 0705.2222 , Bibcode : 2008mgm..conf..126A , doi : 10.1142/9789812834300_0008 , ISBN  978-981-283-426-3 , S2CID   119663169
• Аштекар, Абхай; Кришнан, Бадри (2004), «Изолированные и динамические горизонты и их приложения», Living Reviews in Relativity , 7 (1): 10, arXiv : gr-qc/0407042 , Bibcode : 2004LRR.....7...10A , doi : 10.12942/lrr-2004-10 , PMC   5253930 , PMID   28163644
• Аштекар, Абхай; Левандовски, Ежи (2004), «Фоновая независимая квантовая гравитация: отчет о состоянии», класс. Квантовая гравитация. , 21 (15): R53–R152, arXiv : gr-qc/0404018 , Bibcode : 2004CQGra..21R..53A , doi : 10.1088/0264-9381/21/15/R01 , S2CID   119175535
• Аштекар, Абхай; Магнон-Аштекар, Энн (1979), «О сохраняющихся величинах в общей теории относительности», Journal of Mathematical Physics , 20 (5): 793–800, Бибкод : 1979JMP....20..793A , doi : 10.1063/1.524151
• Ауян, Санни Ю. (1995), Как возможна квантовая теория поля? , Издательство Оксфордского университета, ISBN  978-0-19-509345-2
• Баня, ТМ; Руд, RT; Бальзер, Д.С. (2002), «Космологическая плотность барионов по наблюдениям 3He+ в Млечном Пути», Nature , 415 (6867): 54–57, Бибкод : 2002Natur.415...54B , doi : 10.1038/415054a , ПМИД   11780112 , С2КИД   4303625
• Барак, Леор; Катлер, Курт (2004), «Источники захвата LISA: приблизительные формы сигналов, отношение сигнал/шум и точность оценки параметров», Phys. Rev. , D69 (8): 082005, arXiv : gr-qc/0310125 , Bibcode : 2004PhRvD..69h2005B , doi : 10.1103/PhysRevD.69.082005 , S2CID   21565397
• Бардин, Дж. М. ; Картер, Б .; Хокинг, SW (1973), «Четыре закона механики черных дыр» , Comm. Математика. Физ. , 31 (2): 161–170, Bibcode : 1973CMaPh..31..161B , doi : 10.1007/BF01645742 , S2CID   54690354
• Бариш, Барри (2005), «На пути к обнаружению гравитационных волн», Флоридес, П.; Нолан, Б.; Оттевил А. (ред.), Общая теория относительности и гравитация. Материалы 17-й Международной конференции , World Scientific, стр. 24–34, Bibcode : 2005grg..conf.....F , ISBN  978-981-256-424-5
• Барстоу, М.; Бонд, Ховард Э.; Хольберг, Дж.Б.; Берли, MR; Хубени, И.; Кестер, Д. (2005), «Спектроскопия бальмеровских линий на Сириусе Б космическим телескопом Хаббл», Mon. Нет. Р. Астрон. Соц. , 362 (4): 1134–1142, arXiv : astro-ph/0506600 , Bibcode : 2005MNRAS.362.1134B , doi : 10.1111/j.1365-2966.2005.09359.x , S2CID   4607496
• Бартусяк, Марсия (2000), Неоконченная симфония Эйнштейна: слушая звуки пространства-времени , Беркли, ISBN  978-0-425-18620-6
• Бегельман, Митчелл С.; Бландфорд, Роджер Д .; Рис, Мартин Дж. (1984), «Теория внегалактических радиоисточников», Rev. Mod. Физ. , 56 (2): 255–351, Бибкод : 1984RvMP...56..255B , doi : 10.1103/RevModPhys.56.255
• Бейг, Роберт; Хрушель, Петр Т. (2006), «Стационарные черные дыры», Франсуаза, Ж.-П.; Набер, Г.; Цоу, Т.С. (ред.), Энциклопедия математической физики, том 2 , Elsevier, стр. 2041, arXiv : gr-qc/0502041 , Bibcode : 2005gr.qc.....2041B , ISBN  978-0-12-512660-1
• Бекенштейн, Джейкоб Д. (1973), «Черные дыры и энтропия», Phys. Rev. , D7 (8): 2333–2346, Bibcode : 1973PhRvD...7.2333B , doi : 10.1103/PhysRevD.7.2333 , S2CID   122636624
• Бекенштейн, Джейкоб Д. (1974), «Обобщенный второй закон термодинамики в физике черных дыр», Phys. Rev. , D9 (12): 3292–3300, Bibcode : 1974PhRvD...9.3292B , doi : 10.1103/PhysRevD.9.3292 , S2CID   123043135
• Белинский, В.А.; Халатников И.М. ; Лифшиц, Э.М. (1971), «Колебательный подход к особой точке в релятивистской космологии», Advances in Physics , 19 (80): 525–573, Bibcode : 1970AdPhy..19..525B , doi : 10.1080/00018737000101171 ; оригинал статьи на русском языке: Belinsky, V. A.; Lifshits, I. M.; Khalatnikov, E. M. (1970), "Колебательный Режим Приближения К Особой Точке В Релятивистской Космологии", Uspekhi Fizicheskikh Nauk , 102 (11): 463–500, Bibcode : 1970UsFiN.102..463B , doi : 10.3367/ufnr.0102.197011d.0463
• Беннетт, CL; Халперн, М.; Хиншоу, Г.; Ярошик, Н.; Когут, А.; Лимон, М.; Мейер, СС; Пейдж, Л.; и др. (2003), «Наблюдения первого года обучения с помощью микроволнового зонда анизотропии Уилкинсона (WMAP): предварительные карты и основные результаты», Astrophys. J. Приложение. Сер. , 148 (1): 1–27, arXiv : astro-ph/0302207 , Bibcode : 2003ApJS..148....1B , doi : 10.1086/377253 , S2CID   115601
• Бергер, Беверли К. (2002), «Численные подходы к особенностям пространства-времени», Living Reviews in Relativity , 5 (1): 1, arXiv : gr-qc/0201056 , Bibcode : 2002LRR.....5.... 1B , doi : 10.12942/lrr-2002-1 , PMC   5256073 , PMID   28179859
• Бергстрем, Ларс; Губар, Ариэль (2003), Космология и астрофизика элементарных частиц (2-е изд.), Wiley & Sons, ISBN  978-3-540-43128-2
• Бертотти, Бруно ; Чуфолини, Игнацио; Бендер, Питер Л. (1987), «Новый тест общей теории относительности: измерение скорости геодезической прецессии де Ситтера для перигея Луны», Physical Review Letters , 58 (11): 1062–1065, Бибкод : 1987PhRvL..58.1062B , doi : 10.1103/PhysRevLett.58.1062 , PMID   10034329
• Бертотти, Бруно; Иесс, Л.; Тортора, П. (2003), «Испытание общей теории относительности с использованием радиосвязи с космическим кораблем Кассини», Nature , 425 (6956): 374–376, Бибкод : 2003Natur.425..374B , doi : 10.1038/nature01997 , PMID   14508481 , S2CID   4337125
• Берчингер, Эдмунд (1998), «Моделирование формирования структур во Вселенной», Annu. Преподобный Астрон. Астрофиз. , 36 (1): 599–654, Бибкод : 1998ARA&A..36..599B , ​​doi : 10.1146/annurev.astro.36.1.599
• Биррелл, Северная Дакота; Дэвис, ПК (1984), Квантовые поля в искривленном пространстве , издательство Кембриджского университета, ISBN  978-0-521-27858-4
• Блэр, Дэвид ; Макнамара, Джефф (1997), Рябь на космическом море. В поисках гравитационных волн , Персей, ISBN  978-0-7382-0137-5
• Бланше, Л.; Фэй, Г.; Айер, БР; Синха, С. (2008), «Третья постньютоновская поляризация гравитационных волн и связанные с ней сферические гармонические моды для спирали компактных двойных систем на квазикруговых орбитах», Classical and Quantum Gravity , 25 (16): 165003, arXiv : 0802.1249 , Bibcode : 2008CQGra..25p5003B , doi : 10.1088/0264-9381/25/16/165003 , S2CID   54608927
• Бланше, Люк (2006), «Гравитационное излучение от постньютоновских источников и вдохновляющие компактные двойные системы», Living Reviews in Relativity , 9 (1): 4, Bibcode : 2006LRR.....9....4B , doi : 10.12942/lrr-2006-4 , PMC   5255899 , PMID   28179874
• Бландфорд, Р.Д. (1987), «Астрофизические черные дыры», Хокинг, Стивен В.; Израиль, Вернер (ред.), 300 лет гравитации , Cambridge University Press, стр. 277–329, ISBN.  978-0-521-37976-2
• Бёрнер, Герхард (1993), Ранняя Вселенная. Факты и вымысел , Springer, ISBN  978-0-387-56729-7
• Бранденбергер, Роберт Х. (2008), «Концептуальные проблемы инфляционной космологии и новый подход к формированию космологических структур», Лемуан, Мартин; Мартин, Джером; Питер, Патрик (ред.), Инфляционная космология , Конспект лекций по физике, том. 738, стр. 393–424, arXiv : hep-th/0701111 , Bibcode : 2007LNP...738..393B , doi : 10.1007/978-3-540-74353-8_11 , ISBN  978-3-540-74352-1 , S2CID   18752698
• Бранс, Швейцария ; Дике, Р.Х. (1961), «Принцип Маха и релятивистская теория гравитации», Physical Review , 124 (3): 925–935, Бибкод : 1961PhRv..124..925B , doi : 10.1103/PhysRev.124.925
• Уздечка, Сара Л.; Лахав, Офер; Острайкер, Иеремия П .; Стейнхардт, Пол Дж. (2003), «Точная космология? Еще не все», Science , 299 (5612): 1532–1533, arXiv : astro-ph/0303180 , Bibcode : 2003Sci...299.1532B , doi : 10.1126/ science.1082158 , PMID   12624255 , S2CID   119368762
• Брюа, Ивонн (1962), «Проблема Коши», в Виттене, Луи (ред.), Гравитация: введение в текущие исследования , Wiley, стр. 130, ISBN  978-1-114-29166-9
• Бушерт, Томас (2008), «Темная энергия структуры — отчет о состоянии», Общая теория относительности и гравитации , 40 (2–3): 467–527, arXiv : 0707.2153 , Bibcode : 2008GReGr..40..467B , doi : 10.1007/s10714-007-0554-8 , S2CID   17281664
• Бурас, Р.; Рампп, М.; Янка, Х.-Т.; Кифонидис, К. (2003), «Улучшенные модели коллапса звездного ядра и все еще отсутствие взрывов: чего не хватает?», Phys. Преподобный Летт. , 90 (24): 241101, arxiv : Astro-ph/0303171 , Bibcode : 2003phrvl..90x1101b , doi : 10.1103/physrevlett.90.241101 , PMID   12857181 , S2CID   27632148
• Колдуэлл, Роберт Р. (2004), «Темная энергия», Physics World , 17 (5): 37–42, doi : 10.1088/2058-7058/17/5/36
• Карлип, Стивен (2001), «Квантовая гравитация: отчет о прогрессе», Rep. Prog. Физ. , 64 (8): 885–942, arXiv : gr-qc/0108040 , Bibcode : 2001RPPh...64..885C , doi : 10.1088/0034-4885/64/8/301 , S2CID   118923209
• Кэрролл, Брэдли В.; Остли, Дейл А. (1996), Введение в современную астрофизику , Аддисон-Уэсли, ISBN  978-0-201-54730-6
• Кэрролл, Шон М. (2001), «Космологическая константа», « Живые обзоры относительно относительности » , 4 (1): 1, arXiv : astro-ph/0004075 , Bibcode : 2001LRR.....4....1C , doi : 10.12942/lrr-2001-1 , PMC   5256042 , PMID   28179856
• Картер, Брэндон (1979), «Общая теория механических, электромагнитных и термодинамических свойств черных дыр», в Хокинге, SW; Израиль, В. (ред.), Общая теория относительности, обзор столетия Эйнштейна , Cambridge University Press, стр. 294–369 и 860–863, ISBN.  978-0-521-29928-2
• Челотти, Анналиса; Миллер, Джон К.; Скиама, Деннис В. (1999), «Астрофизические доказательства существования черных дыр», Класс. Квантовая гравитация. , 16 (12A): A3–A21, arXiv : astro-ph/9912186 , Bibcode : 1999CQGra..16A...3C , doi : 10.1088/0264-9381/16/12A/301 , S2CID   17677758
• Чандрасекар, Субраманян (1983), Математическая теория черных дыр , Нью-Йорк: Oxford University Press, ISBN  978-0-19-850370-5
• Чандрасекхар, Субрахманьян (1984), «Общая теория относительности - почему« это, вероятно, самая красивая из всех существующих теорий » », Журнал астрофизики и астрономии , 5 (1): 3–11, Bibcode : 1984JApA ... .5....3C , doi : 10.1007/BF02714967 , S2CID   120910934
• Шарбоннель, К.; Примас, Ф. (2005), «Содержание лития в звездах галактического гало», Astronomy & Astrophysicals , 442 (3): 961–992, arXiv : astro-ph/0505247 , Bibcode : 2005A&A...442..961C , doi : 10.1051/0004-6361:20042491 , S2CID   119340132
• Чуфолини, Игнацио; Павлис, Эррикос К. (2004), «Подтверждение общего релятивистского предсказания эффекта Лензе-Тирринга», Nature , 431 (7011): 958–960, Бибкод : 2004Natur.431..958C , doi : 10.1038/nature03007 , PMID   15496915 , S2CID   4423434
• Чуфолини, Игнацио; Павлис, Эррикос К.; Перон, Р. (2006), «Определение перетаскивания кадров с использованием моделей земной гравитации от CHAMP и GRACE», New Astron. , 11 (8): 527–550, Бибкод : 2006NewA...11..527C , doi : 10.1016/j.newast.2006.02.001
• Кок, А.; Ванджиони-Флам, Элизабет; Декувемон, Пьер; Адачур, Абдеррахим; Ангуло, Кармен (2004), «Обновленный нуклеосинтез Большого взрыва в сравнении с наблюдениями WMAP и изобилием легких элементов», Astrophysical Journal , 600 (2): 544–552, arXiv : astro-ph/0309480 , Bibcode : 2004ApJ.. .600..544C , doi : 10.1086/380121 , S2CID   16276658
• Катлер, Курт; Торн, Кип С. (2002), «Обзор источников гравитационных волн», Бишоп, Найджел; Махарадж, Сунил Д. (ред.), Труды 16-й Международной конференции по общей теории относительности и гравитации (GR16) , World Scientific, с. 4090, arXiv : gr-qc/0204090 , Bibcode : 2002gr.qc.....4090C , ISBN  978-981-238-171-2
• Далал, Нил; Хольц, Дэниел Э.; Хьюз, Скотт А.; Джайн, Бхувнеш (2006), «Короткие гамма-всплески и стандартные сирены бинарных черных дыр как зонд темной энергии», Phys. Rev. D , 74 (6): 063006, arXiv : astro-ph/0601275 , Bibcode : 2006PhRvD..74f3006D , doi : 10.1103/PhysRevD.74.063006 , S2CID   10008243
• Данцманн, Карстен; Рюдигер, Альбрехт (2003), «Технология LISA — концепции, статус, перспективы» (PDF) , Класс. Квантовая гравитация. , 20 (10): S1–S9, Bibcode : 2003CQGra..20S...1D , doi : 10.1088/0264-9381/20/10/301 , hdl : 11858/00-001M-0000-0013-5233-E , S2CID   250836327 , заархивировано из оригинала (PDF) 26 сентября 2007 г.
• Донохью, Джон Ф. (1995), «Введение в описание гравитации эффективной теорией поля», в Корне, Фернандо (редактор), «Эффективные теории: материалы высшей школы», Альмунекар, Испания, 26 июня – 1 июля 1995 г. , Сингапур: World Scientific, с. 12024, arXiv : gr-qc/9512024 , Bibcode : 1995gr.qc....12024D , ISBN  978-981-02-2908-5
• Дедиу, Адриан-Хориа; Магдалена, Луис; Мартин-Виде, Карлос, ред. (2015). Теория и практика естественных вычислений: Четвертая международная конференция, TPNC 2015, Мьерес, Испания, 15–16 декабря 2015 г. Труды . Спрингер. ISBN  978-3-319-26841-5 .
• Дафф, Майкл (1996), «М-теория (теория, ранее известная как струны)», Int. Дж. Мод. Физ. A , 11 (32): 5623–5641, arXiv : hep-th/9608117 , Bibcode : 1996IJMPA..11.5623D , doi : 10.1142/S0217751X96002583 , S2CID   17432791
• Элерс, Юрген (1973), «Обзор общей теории относительности», в Израиле, Вернер (редактор), «Относительность, астрофизика и космология» , Д. Рейдель, стр. 1–125, ISBN  978-90-277-0369-9
• Элерс, Юрген; Фалько, Эмилио Э.; Шнайдер, Питер (1992), Гравитационные линзы , Springer, ISBN  978-3-540-66506-9
• Элерс, Юрген; Леммерцаль, Клаус, ред. (2006), Специальная теория относительности: сохранится ли она в ближайшие 101 год? , Спрингер, ISBN  978-3-540-34522-0
• Элерс, Юрген; Риндлер, Вольфганг (1997), «Локальный и глобальный изгиб света в теориях Эйнштейна и других теориях гравитации», Общая теория относительности и гравитации , 29 (4): 519–529, Бибкод : 1997GReGr..29..519E , doi : 10.1023/A :1018843001842 , hdl : 11858/00-001M-0000-0013-5AB5-4 , S2CID   118162303
• Эйнштейн, Альберт (1907), «О принципе относительности и выводах, сделанных из него» , Ежегодник радиоактивности и электроники , 4 : 411. См. также английский перевод в Einstein Papers Project.

• Эйнштейн, Альберт (1915), «Уравнения гравитации поля» , труды Прусской академии наук в Берлине : 844–847. См. Также английский перевод в Einstein Papers Project.
• Эйнштейн, Альберт (1917), «Космологические соображения по общей теории относительности» , труды Прусской академии наук : 142. См. также английский перевод в проекте Einstein Papers Project.
• Эллис, Джордж Франция ; Ван Эльст, Хенк (1999), «Космологические модели», в Лашез-Рей, Марк (ред.), Теоретическая и наблюдательная космология , том. 541, стр. 1–116, arXiv : gr-qc/9812046 , Bibcode : 1999ASIC..541....1E , doi : 10.1007/978-94-011-4455-1_1 , ISBN  978-0-7923-5946-3 , S2CID   122994560
• Энглер, Гидеон (2002), «Эйнштейн и самые красивые теории физики», Международные исследования в области философии науки , 16 (1): 27–37, doi : 10.1080/02698590120118800 , S2CID   120160056
• Эверитт, CWF; Бухман, С.; ДеБра, Д.Б.; Кейзер, генеральный директор (2001), «Гравитационный зонд B: обратный отсчет до запуска», в Лэммерцале, К.; Эверитт, CWF; Хель, Ф.В. (ред.), Гироскопы, часы и интерферометры: проверка релятивистской гравитации в космосе (конспекты лекций по физике 562) , Springer, стр. 52–82, ISBN  978-3-540-41236-6
• Эверитт, CWF; Паркинсон, Брэдфорд; Кан, Боб (2007), Эксперимент «Гравитационный зонд B». Анализ после полета — окончательный отчет (предисловие и краткое изложение) (PDF) , отчет о проекте: НАСА, Стэнфордский университет и Lockheed Martin, заархивировано (PDF) из оригинала 9 июня 2007 г. , получено 5 августа 2007 г.
• Фальке, Хейно; Мелия, Фульвио; Агол, Эрик (2000), «Просмотр тени черной дыры в галактическом центре», Astrophysical Journal , 528 (1): L13–L16, arXiv : astro-ph/9912263 , Bibcode : 2000ApJ...528L.. 13F , doi : 10.1086/312423 , PMID   10587484 , S2CID   119433133
• Фонт, Хосе А. (2003), «Численная гидродинамика в общей теории относительности», Living Reviews in Relativity , 6 (1): 4, Bibcode : 2003LRR.....6....4F , doi : 10.12942/lrr- 2003-4 , ПМЦ   5660627 , ПМИД   29104452
• Фурес-Брюа, Ивонн (1952), «Теорема существования некоторых систем нелинейных уравнений в частных производных», Acta Mathematica , 88 (1): 141–225, Бибкод : 1952AcMa...88..141F , doi : 10.1007/BF02392131
• Фрауэндинер, Йорг (2004), «Конформная бесконечность», Living Reviews in Relativity , 7 (1): 1, Bibcode : 2004LRR.....7....1F , doi : 10.12942/lrr-2004-1 , PMC   5256109 , ПМИД   28179863
• Фридрих, Хельмут (2005), «Является ли общая теория относительности «по существу понятной»?», Annalen der Physik , 15 (1–2): 84–108, arXiv : gr-qc/0508016 , Bibcode : 2006AnP...518.. .84F , doi : 10.1002/andp.200510173 , S2CID   37236624
• Футамасе, Т.; Ито, Ю. (2006), «Постньютоновское приближение для релятивистских компактных двойных систем», Living Reviews in Relativity , 10 (1): 2, Bibcode : 2007LRR....10....2F , doi : 10.12942/ lrr-2007-2 , PMC   5255906 , PMID   28179819
• Гамов, Георгий (1970), Моя мировая линия , Viking Press, ISBN  978-0-670-50376-6
• Гарфинкл, Дэвид (2007), «О сингулярностях и хлебопечении» , Einstein Online , Институт гравитационной физики Макса Планка , заархивировано из оригинала 10 августа 2007 г. , получено 3 августа 2007 г.
• Герох, Роберт (1996). «Уравнения физики в частных производных». Общая теория относительности : 19. arXiv : gr-qc/9602055 . Бибкод : 1996gere.conf...19G .
• Джулини, Доменико (2005), Специальная теория относительности: первая встреча , Oxford University Press, ISBN  978-0-19-856746-2
• Джулини, Доменико (2006), «Алгебраические и геометрические структуры в специальной теории относительности», в Элерсе, Юргене; Лэммерзал, Клаус (ред.), Специальная теория относительности: просуществует ли она в ближайшие 101 год? , Конспект лекций по физике, вып. 702, стр. 45–111, arXiv : math-ph/0602018 , Bibcode : 2006math.ph...2018G , doi : 10.1007/3-540-34523-X_4 , ISBN  978-3-540-34522-0 , S2CID   15948765
• Джулини, Доменико (2007), «Замечания о понятиях общей ковариации и независимости от фона», в Стаматеску, И.О. (ред.), Подходы к фундаментальной физике , Конспекты лекций по физике, том. 721, стр. 105–120, arXiv : gr-qc/0603087 , Bibcode : 2007LNP...721..105G , doi : 10.1007/978-3-540-71117-9_6 , ISBN  978-3-540-71115-5 , S2CID   14772226
• Гнедин, Николай Ю. (2005), «Оцифровка Вселенной», Nature , 435 (7042): 572–573, Bibcode : 2005Natur.435..572G , doi : 10.1038/435572a , PMID   15931201 , S2CID   3023436
• Гённер, Хьюберт Ф.М. (2004), «К истории единых теорий поля», Living Reviews in Relativity , 7 (1): 2, Bibcode : 2004LRR.....7....2G , doi : 10.12942/lrr -2004-2 , ПМК   5256024 , ПМИД   28179864
• Горофф, Марк Х.; Саньотти, Аугусто (1985), «Квантовая гравитация в двух петлях», Phys. Летт. , 160Б (1–3): 81–86, Бибкод : 1985PhLB..160...81G , doi : 10.1016/0370-2693(85)91470-4
• Гургульон, Эрик (2007). «Формализм 3 + 1 и основы числовой относительности». arXiv : gr-qc/0703035 .
• Гауди, Роберт Х. (1971), «Гравитационные волны в закрытых вселенных», Phys. Преподобный Летт. , 27 (12): 826–829, Бибкод : 1971PhRvL..27..826G , doi : 10.1103/PhysRevLett.27.826
• Гауди, Роберт Х. (1974), «Вакуумное пространство-время с двухпараметрическими пространственноподобными группами изометрий и компактными инвариантными гиперповерхностями: топологии и граничные условия», Annals of Physics , 83 (1): 203–241, Bibcode : 1974AnPhy..83. .203G , doi : 10.1016/0003-4916(74)90384-4
• Грин, МБ ; Шварц, Дж. Х. ; Виттен, Э. (1987), Теория суперструн. Том 1: Введение , Издательство Кембриджского университета, ISBN  978-0-521-35752-4
• Гринштейн, Дж.Л.; Ок, Джей Би; Шипман, Х.Л. (1971), «Эффективная температура, радиус и гравитационное красное смещение Сириуса B», Astrophysical Journal , 169 : 563, Бибкод : 1971ApJ...169..563G , doi : 10.1086/151174
• Хамбер, Герберт В. (2009), Хамбер, Герберт В. (ред.), Квантовая гравитация - интегральный подход пути Фейнмана , Springer Publishing, doi : 10.1007/978-3-540-85293-3 , hdl : 11858/00- 001М-0000-0013-471Д-А , ISBN  978-3-540-85292-6
• Гёдель, Курт (1949). «Пример нового типа космологического решения уравнений поля гравитации Эйнштейна» . Преподобный Мод. Физ . 21 (3): 447–450. Бибкод : 1949РвМП...21..447Г . дои : 10.1103/RevModPhys.21.447 .
• Хафеле, JC ; Китинг, Р.Э. (14 июля 1972 г.). «Вокругсветные атомные часы: предсказанный релятивистский выигрыш во времени». Наука . 177 (4044): 166–168. Бибкод : 1972Sci...177..166H . дои : 10.1126/science.177.4044.166 . ПМИД   17779917 . S2CID   10067969 .
• Хафеле, JC ; Китинг, Р.Э. (14 июля 1972 г.). «Вокругсветные атомные часы: наблюдаемый релятивистский выигрыш во времени». Наука . 177 (4044): 168–170. Бибкод : 1972Sci...177..168H . дои : 10.1126/science.177.4044.168 . ПМИД   17779918 . S2CID   37376002 .
• Хавас, П. (1964), «Четырехмерная формулировка ньютоновской механики и их связь со специальной и общей теорией относительности», Rev. Mod. Физ. , 36 (4): 938–965, Бибкод : 1964RvMP...36..938H , doi : 10.1103/RevModPhys.36.938
• Хокинг, Стивен В. (1966), «Возникновение сингулярностей в космологии», Труды Королевского общества , A294 (1439): 511–521, Бибкод : 1966RSPSA.294..511H , doi : 10.1098/rspa.1966.0221 , JSTOR   2415489 , S2CID   120730123
• Хокинг, SW (1975), «Создание частиц черными дырами» , Communications in Mathematical Physics , 43 (3): 199–220, Bibcode : 1975CMaPh..43..199H , doi : 10.1007/BF02345020 , S2CID   55539246
• Хокинг, Стивен В. (1987), «Квантовая космология», Хокинг, Стивен В.; Израиль, Вернер (ред.), 300 лет гравитации , Cambridge University Press, стр. 631–651, ISBN.  978-0-521-37976-2
• Хокинг, Стивен В.; Эллис, Джордж Ф.Р. (1973), Крупномасштабная структура пространства-времени , Cambridge University Press, ISBN  978-0-521-09906-6
• Хекман, ОХЛ; Шюкинг, Э. (1959), «Ньютоновская и эйнштейновская космология», в Флюгге, С. (ред.), Энциклопедия физики , том. 53, с. 489
• Хойслер, Маркус (1998), «Стационарные черные дыры: уникальность и не только», Living Reviews in Relativity , 1 (1): 6, Bibcode : 1998LRR.....1....6H , doi : 10.12942/lrr- 1998-6 , ПМЦ   5567259 , ПМИД   28937184
• Хойслер, Маркус (1996), Теоремы уникальности черной дыры , издательство Кембриджского университета, ISBN  978-0-521-56735-0
• Привет, Тони; Уолтерс, Патрик (2003), Новая квантовая вселенная , Cambridge University Press, Bibcode : 2003nqu..book.....H , ISBN  978-0-521-56457-1
• Хаф, Джим; Роуэн, Шейла (2000), «Обнаружение гравитационных волн с помощью интерферометрии (Земля и космос)», Living Reviews in Relativity , 3 (1): 3, Бибкод : 2000LRR.....3....3R , doi : 10.12942 /lrr-2000-3 , PMC   5255574 , PMID   28179855
• Хаббл, Эдвин (1929), «Связь между расстоянием и лучевой скоростью среди внегалактических туманностей», Proc. Натл. акад. наук. , 15 (3): 168–173, Бибкод : 1929PNAS...15..168H , doi : 10.1073/pnas.15.3.168 , PMC   522427 , PMID   16577160
• Халс, Рассел А .; Тейлор, Джозеф Х. (1975), «Открытие пульсара в двойной системе», Astrophys. J. , 195 : L51–L55, Bibcode : 1975ApJ...195L..51H , doi : 10.1086/181708
• Ибанез, Л.Е. (2000), «Вторая струнная (феноменологическая) революция», Класс. Квантовая гравитация. , 17 (5): 1117–1128, arXiv : hep-ph/9911499 , Bibcode : 2000CQGra..17.1117I , doi : 10.1088/0264-9381/17/5/321 , S2CID   15707877
• Иорио, Л. (2006), «Заметка о доказательствах гравитомагнитного поля Марса», Classical and Quantum Gravity , 23 (17): 5451–5454, arXiv : gr-qc/0606092 , Bibcode : 2006CQGra..23.5451 Я , doi : 10.1088/0264-9381/23/17/N01 , S2CID   118233440
• Иорио, Л. (2009), «Оценка систематической неопределенности в настоящих и будущих испытаниях эффекта линзы-Тирринга с помощью спутниковой лазерной локации», Space Sci. Rev. , 148 (1–4): 363–381, arXiv : 0809.1373 , Bibcode : 2009SSRv..148..363I , doi : 10.1007/s11214-008-9478-1 , S2CID   15698399
• Иорио, Л. (2010), «Об тесте Лензе-Тирринга с Mars Global Surveyor в гравитационном поле Марса», Central European Journal of Physics , 8 (3): 509–513, arXiv : gr-qc/0701146 , Bibcode : 2010CEJPh...8..509I , doi : 10.2478/s11534-009-0117-6 , S2CID   16052420
• Ишам, Кристофер Дж. (1994), «Вопросы на первый взгляд в квантовой гравитации», у Элерса, Юргена; Фридрих, Хельмут (ред.), Каноническая гравитация: от классической к квантовой , Springer, ISBN  978-3-540-58339-4
• Израиль, Вернер (1971), «Горизонты событий и гравитационный коллапс», Общая теория относительности и гравитация , 2 (1): 53–59, Бибкод : 1971GReGr...2...53I , doi : 10.1007/BF02450518 , S2CID   119645546
• Израиль, Вернер (1987), «Темные звезды: эволюция идеи», Хокинг, Стивен В.; Израиль, Вернер (ред.), 300 лет гравитации , Cambridge University Press, стр. 199–276, ISBN.  978-0-521-37976-2
• Янссен, Мишель (2005), «О горшках и дырах: ухабистая дорога Эйнштейна к общей теории относительности» , Annalen der Physik , 14 (S1): 58–85, Бибкод : 2005AnP...517S..58J , doi : 10.1002/andp .200410130 , S2CID   10641693 , заархивировано из оригинала (PDF) 25 августа 2020 г. , получено 28 августа 2010 г.
• Ярановский, Петр; Крулак, Анджей (2005), «Анализ гравитационно-волновых данных. Формализм и примеры приложений: случай Гаусса», Living Reviews in Relativity , 8 (1): 3, Bibcode : 2005LRR.....8....3J , doi : 10.12942/lrr-2005-3 , PMC   5253919 , PMID   28163647
• Кан, Боб (1996–2012), Веб-сайт Gravity Probe B , Стэнфордский университет , получено 20 апреля 2012 г.
• Кан, Боб (14 апреля 2007 г.), Был ли прав Эйнштейн? Ученые впервые публично ознакомились с результатами гравитационного зонда B (пресс-релиз Стэнфордского университета) (PDF) , Служба новостей Стэнфордского университета, заархивировано (PDF) с оригинала 23 апреля 2007 г.
• Камионковски, Марк; Косовский, Артур; Стеббинс, Альберт (1997), «Статистика фоновой поляризации космического микроволнового излучения», Phys. Rev. , D55 (12): 7368–7388, arXiv : astro-ph/9611125 , Bibcode : 1997PhRvD..55.7368K , doi : 10.1103/PhysRevD.55.7368 , S2CID   14018215
• Кеннефик, Дэниел (2005), «Астрономы проверяют общую теорию относительности: изгиб света и красное смещение Солнца», в Ренне, Юрген (ред.), Сто авторов Эйнштейна , Wiley-VCH, стр. 178–181, ISBN  978-3-527-40574-9
• Кеннефик, Дэниел (2007), «Не только из-за теории: Дайсон, Эддингтон и конкурирующие мифы об экспедиции затмения 1919 года», Материалы 7-й конференции по истории общей теории относительности, Тенерифе, 2005 , том. 0709, с. 685, arXiv : 0709.0685 , Bibcode : 2007arXiv0709.0685K , doi : 10.1016/j.shpsa.2012.07.010 , S2CID   119203172
• Кеньон, IR (1990), Общая теория относительности , Oxford University Press, ISBN  978-0-19-851996-6
• Кочанек, CS; Фалько, Э.Э.; Импи, К.; Лехар, Дж. (2007), Веб-сайт исследования CASTLES , Гарвард-Смитсоновский центр астрофизики , получено 21 августа 2007 г.
• Комар, Артур (1959), «Ковариантные законы сохранения в общей теории относительности», Phys. Rev. , 113 (3): 934–936, Bibcode : 1959PhRv..113..934K , doi : 10.1103/PhysRev.113.934
• Крамер, Майкл (2004). «Инструменты фундаментальной физики миллисекундных пульсаров». В Каршенбойме, СГ; Пейк, Э. (ред.). Астрофизика, часы и фундаментальные константы . Конспект лекций по физике. Том. 648. стр. 33–54. arXiv : astro-ph/0405178 . Бибкод : 2004ЛНП...648...33К . дои : 10.1007/978-3-540-40991-5_3 . ISBN  978-3-540-21967-5 .
• Крамер, М.; Лестница, IH; Манчестер, штат РН; Маклафлин, Массачусетс; Лайн, АГ; Фердман, Р.Д.; Бургай, М.; Лоример, доктор медицинских наук; и др. (2006), «Испытания общей теории относительности по времени двойного пульсара», Science , 314 (5796): 97–102, arXiv : astro-ph/0609417 , Bibcode : 2006Sci...314...97K , doi : 10.1126 /science.1132305 , PMID   16973838 , S2CID   6674714
• Краус, Юте (1998), «Отклонение света вблизи нейтронных звезд», Релятивистская астрофизика , Vieweg, стр. 66–81, ISBN  978-3-528-06909-4
• Кухарж, Карел (1973), «Каноническое квантование гравитации», в Израиле, Вернер (редактор), «Относительность, астрофизика и космология» , Д. Рейдель, стр. 237–288, ISBN  978-90-277-0369-9
• Кюнцле, HP (1972), «Структуры Галилея и Лоренца в пространстве-времени: сравнение соответствующей геометрии и физики» , Annales de l'Institut Henri Poincaré A , 17 : 337–362
• Лахав, Офер; Суто, Ясуши (2004), «Измерение нашей Вселенной на основе исследований красного смещения галактик», Living Reviews in Relativity , 7 (1): 8, arXiv : astro-ph/0310642 , Bibcode : 2004LRR.....7.... 8L , doi : 10.12942/lrr-2004-8 , PMC   5253994 , PMID   28163643
• Ландау, Л.Д.; Лифшиц, Э.М. (1975), Классическая теория полей, т. 2 , Elsevier Science, Ltd., ISBN  978-0-08-018176-9
• Ленер, Луис (2001), «Численная относительность: обзор», Класс. Квантовая гравитация. , 18 (17): R25–R86, arXiv : gr-qc/0106072 , Bibcode : 2001CQGra..18R..25L , doi : 10.1088/0264-9381/18/17/202 , S2CID   9715975
• Ленер, Луис (2002). «Численная теория относительности: состояние и перспективы». У Найджела Т. Бишопа; Сунил Д. Махарадж (ред.). Общая теория относительности и гравитация . Общая теория относительности и гравитация: материалы 16-й Международной конференции, Дурбан, Южная Африка, 15–21 июля 2001 г., с. 210. arXiv : gr-qc/0202055 . Бибкод : 2002grg..conf..210L . дои : 10.1142/9789812776556_0010 . ISBN  978-981-238-171-2 . S2CID   9145148 .
• Линде, Андрей (2005), «Физика элементарных частиц и инфляционная космология», Contemp.concepts Phys , 5 : 1–362, arXiv : hep-th/0503203 , Bibcode : 2005hep.th....3203L , ISBN  978-3-7186-0489-0
• Линде, Андрей (2006), «На пути к инфляции в теории струн», J. Phys. Конф. Сер. , 24 (1): 151–160, arXiv : hep-th/0503195 , Bibcode : 2005JPhCS..24..151L , doi : 10.1088/1742-6596/24/1/018 , S2CID   250677699
• Лолл, Рената (1998), «Дискретные подходы к квантовой гравитации в четырех измерениях», Living Reviews in Relativity , 1 (1): 13, arXiv : gr-qc/9805049 , Bibcode : 1998LRR.....1... 13L , doi : 10.12942/lrr-1998-13 , PMC   5253799 , PMID   28191826
• Лавлок, Дэвид (1972), «Четырехмерность пространства и тензор Эйнштейна», J. Math. Физ. , 13 (6): 874–876, Бибкод : 1972JMP....13..874L , doi : 10.1063/1.1666069
• МакКаллум, М. (2006), «Нахождение и использование точных решений уравнений Эйнштейна», Морнас, Л.; Алонсо, доктор медицинских наук (ред.), Материалы конференции AIP (Век физики относительности: ERE05, XXVIII Испанское собрание по теории относительности), том. 841, стр. 129–143, arXiv : gr-qc/0601102 , Bibcode : 2006AIPC..841..129M , doi : 10.1063/1.2218172 , S2CID   13096531
• Мэддокс, Джон (1998), Что еще предстоит открыть , Macmillan, ISBN  978-0-684-82292-1
• Мангейм, Филип Д. (2006), «Альтернативы темной материи и темной энергии», Prog. Часть. Нукл. Физ. , 56 (2): 340–445, arXiv : astro-ph/0505266 , Bibcode : 2006PrPNP..56..340M , doi : 10.1016/j.ppnp.2005.08.001 , S2CID   14024934
• Мэзер, Джей Си ; Ченг, ES; Коттингем, Вашингтон; Эпли, RE; Фикссен, диджей; Хевагама, Т.; Исаакман, РБ; Дженсен, Калифорния; и др. (1994), «Измерение космического микроволнового спектра прибором COBE FIRAS», Astrophysical Journal , 420 : 439–444, Бибкод : 1994ApJ...420..439M , doi : 10.1086/173574
• Мермин, Н. Дэвид (2005), Пришло время. Понимание относительности Эйнштейна , Princeton University Press, ISBN  978-0-691-12201-4
• Мессия, Альберт (1999), Квантовая механика , Dover Publications, ISBN  978-0-486-40924-5
• Миллер, Коул (2002), Звездная структура и эволюция (конспекты лекций по астрономии 606) , Университет Мэриленда , получено 25 июля 2007 г.
• Миснер, Чарльз В .; Торн, Кип. С .; Уиллер, Джон А. (1973), Гравитация , WH Freeman, ISBN  978-0-7167-0344-0
• Нараян, Рамеш (2006), «Черные дыры в астрофизике», New Journal of Physics , 7 (1): 199, arXiv : gr-qc/0506078 , Bibcode : 2005NJPh....7..199N , doi : 10.1088/ 1367-2630/7/1/199 , S2CID   17986323
• Нараян, Рамеш; Бартельманн, Матиас (1997). «Лекции по гравитационному линзированию». arXiv : astro-ph/9606001 .
• Нарликар, Джаянт В. (1993), Введение в космологию , издательство Кембриджского университета, ISBN  978-0-521-41250-6
• Нордстрем, Гуннар (1918), «Об энергии гравитационного поля в теории Эйнштейна», Verhandl. Конинкл. Нед. Акад. Ветеншап. , 26 : 1238–1245, Бибкод : 1918KNAB...20.1238N
• Нордтведт, Кеннет (2003). «Лунная лазерная локация - комплексное исследование постньютоновской гравитации». arXiv : gr-qc/0301024 .
• Нортон, Джон Д. (1985), «В чем заключался принцип эквивалентности Эйнштейна?» (PDF) , Исследования по истории и философии науки , 16 (3): 203–246, Бибкод : 1985SHPSA..16..203N , doi : 10.1016/0039-3681(85)90002-0 , в архиве (PDF) с сайта оригинал 22 сентября 2006 г. , получено 11 июня 2007 г.
• Оганян, Ханс К.; Руффини, Ремо (1994), Гравитация и пространство-время , WW Norton & Company, ISBN  978-0-393-96501-8
• Олив, Калифорния; Скиллман, Е.А. (2004), «Реалистическое определение ошибки относительно содержания первичного гелия», Astrophysical Journal , 617 (1): 29–49, arXiv : astro-ph/0405588 , Bibcode : 2004ApJ...617.. .29O , doi : 10.1086/425170 , S2CID   15187664
• О'Мира, Джон М.; Титлер, Дэвид; Киркман, Дэвид; Сузуки, Нао; Прочаска, Джейсон X.; Любин, Дэн; Вулф, Артур М. (2001), «Отношение содержания дейтерия к водороду на пути к четвертому QSO: HS0105 + 1619», Astrophysical Journal , 552 (2): 718–730, arXiv : astro-ph/0011179 , Bibcode : 2001ApJ. ..552..718O , doi : 10.1086/320579 , S2CID   14164537
• Оппенгеймер, Дж. Роберт ; Снайдер, Х. (1939), «О продолжающемся гравитационном сжатии», Physical Review , 56 (5): 455–459, Бибкод : 1939PhRv...56..455O , doi : 10.1103/PhysRev.56.455
• Овербай, Деннис (1999), Одинокие сердца космоса: история научных поисков тайны Вселенной , Бэк-Бэй, ISBN  978-0-316-64896-7
• Пайс, Авраам (1982), «Тонок Господь…» Наука и жизнь Альберта Эйнштейна , Oxford University Press, ISBN  978-0-19-853907-0
• Пикок, Джон А. (1999), Космологическая физика , издательство Кембриджского университета, ISBN  978-0-521-41072-4
• Пиблз, PJE (1966), «Изобилие первичного гелия и первичный огненный шар II», Astrophysical Journal , 146 : 542–552, Бибкод : 1966ApJ...146..542P , doi : 10.1086/148918
• Пиблс, PJE (1993), Принципы физической космологии , Princeton University Press, ISBN  978-0-691-01933-8
• Пиблс, PJE; Шрамм, Д.Н.; Тернер, Эл.; Крон, Р.Г. (1991), «Доводы в пользу релятивистской космологии горячего Большого взрыва», Nature , 352 (6338): 769–776, Бибкод : 1991Natur.352..769P , doi : 10.1038/352769a0 , S2CID   4337502
• Пенроуз, Роджер (1965), «Гравитационный коллапс и сингулярности пространства-времени», Physical Review Letters , 14 (3): 57–59, Бибкод : 1965PhRvL..14...57P , doi : 10.1103/PhysRevLett.14.57
• Пенроуз, Роджер (1969), «Гравитационный коллапс: роль общей теории относительности», Rivista del Nuovo Cimento , 1 : 252–276, Бибкод : 1969NCimR...1..252P
• Пенроуз, Роджер (2004), Дорога к реальности , А. А. Кнопф, ISBN  978-0-679-45443-4
• Пензиас, АА ; Уилсон, Р.В. (1965), «Измерение избыточной температуры антенны при 4080 Мгц/с», Astrophysical Journal , 142 : 419–421, Бибкод : 1965ApJ...142..419P , doi : 10.1086/148307
• Пескин, Майкл Э .; Шредер, Дэниел В. (1995), Введение в квантовую теорию поля , Аддисон-Уэсли, ISBN  978-0-201-50397-5
• Пескин, Майкл Э. (2007), «Темная материя и физика элементарных частиц», Журнал Физического общества Японии , 76 (11): 111017, arXiv : 0707.1536 , Bibcode : 2007JPSJ...76k1017P , doi : 10.1143/JPSJ. 76.111017 , S2CID   16276112
• Пуанкаре, М.Х. (1905), «О динамике электрона», Еженедельные отчеты сессий Академии наук , 140 : 1504–1508.
• Пуассон, Эрик (27 мая 2004 г.). «Движение точечных частиц в искривленном пространстве-времени» . Живые обзоры в теории относительности . 7 (1). 6. arXiv : gr-qc/0306052 . Бибкод : 2004LRR.....7....6P . дои : 10.12942/lrr-2004-6 . ПМК   5256043 . ПМИД   28179866 .
• Пуассон, Эрик (2004), Инструментарий релятивиста. Математика механики черных дыр , издательство Кембриджского университета, бибкод : 2004rtmb.book.....P , ISBN  978-0-521-83091-1
• Полчински, Джозеф (1998a), Теория струн, том. I: Введение в бозонную струну , Издательство Кембриджского университета, ISBN  978-0-521-63303-1
• Полчински, Джозеф (1998b), Теория струн, том. II: Теория суперструн и не только , Издательство Кембриджского университета, ISBN  978-0-521-63304-8
• Паунд, Р.В.; Ребка, Г.А. (1959), «Гравитационное красное смещение в ядерном резонансе», Physical Review Letters , 3 (9): 439–441, Бибкод : 1959PhRvL...3..439P , doi : 10.1103/PhysRevLett.3.439
• Паунд, Р.В.; Ребка Г.А. (1960), "Кажущийся вес фотонов", Физ. Преподобный Летт. , 4 (7): 337–341, Бибкод : 1960PhRvL...4..337P , doi : 10.1103/PhysRevLett.4.337
• Паунд, Р.В.; Снайдер, Дж.Л. (1964), "Влияние гравитации на ядерный резонанс", Phys. Преподобный Летт. , 13 (18): 539–540, Бибкод : 1964PhRvL..13..539P , doi : 10.1103/PhysRevLett.13.539
• Рамон, Пьер (1990), Теория поля: современный учебник , Аддисон-Уэсли, ISBN  978-0-201-54611-8
• Рис, Мартин (1966), «Появление релятивистски расширяющихся радиоисточников», Nature , 211 (5048): 468–470, Бибкод : 1966Natur.211..468R , doi : 10.1038/211468a0 , S2CID   41065207
• Рейсснер, Х. (1916), «О самогравитации электрического поля согласно теории Эйнштейна» , Annals of Physics , 355 (9): 106–120, Бибкод : 1916AnP...355..106R , doi : 10.1002/андп .19163550905
• Ремиллард, Рональд А.; Линь, Даченг; Купер, Рэндалл Л.; Нараян, Рамеш (2006), «Скорость рентгеновских всплесков типа I от переходных процессов, наблюдаемых с помощью RXTE: данные о горизонтах событий черных дыр», Astrophysical Journal , 646 (1): 407–419, arXiv : astro-ph/0509758 , Bibcode : 2006ApJ...646..407R , doi : 10.1086/504862 , S2CID   14949527
• Ренн, Юрген, изд. (2007), Генезис общей теории относительности (4 тома) , Дордрехт: Springer, ISBN  978-1-4020-3999-7
• Ренн, Юрген, изд. (2005), Альберт Эйнштейн - главный инженер Вселенной: жизнь и работа Эйнштейна в контексте , Берлин: Wiley-VCH, ISBN  978-3-527-40571-8
• Реула, Оскар А. (1998), «Гиперболические методы для уравнений Эйнштейна», Living Reviews in Relativity , 1 (1): 3, Bibcode : 1998LRR.....1....3R , doi : 10.12942/lrr- 1998-3 , ПМЦ   5253804 , ПМИД   28191833
• Риндлер, Вольфганг (2001), Относительность. Специальный, общий и космологический , Oxford University Press, ISBN  978-0-19-850836-6
• Риндлер, Вольфганг (1991), Введение в специальную теорию относительности , Clarendon Press, Oxford, ISBN  978-0-19-853952-0
• Робсон, Ян (1996), Активные ядра галактик , Джон Уайли, ISBN  978-0-471-95853-6
• Руле, Э.; Моллерах, С. (1997), «Микролинзирование», Physics Reports , 279 (2): 67–118, arXiv : astro-ph/9603119 , Bibcode : 1997PhR...279...67R , doi : 10.1016/S0370- 1573(96)00020-8 , S2CID   262685723
• Ровелли, Карло, изд. (2015), Общая теория относительности: самая красивая из теорий (Исследования де Грюйтера по математической физике) , Бостон: Walter de Gruyter GmbH, ISBN  978-3-11-034042-6
• Ровелли, Карло (2000). «Заметки к краткой истории квантовой гравитации». arXiv : gr-qc/0006061 .
• Ровелли, Карло (1998), «Петлевая квантовая гравитация», « Живые обзоры относительно относительности » , 1 (1): 1, arXiv : gr-qc/9710008 , Bibcode : 1998LRR.....1....1R , CiteSeerX   10.1 .1.90.7036 , doi : 10.12942/lrr-1998-1 , PMC   5567241 , PMID   28937180
• Шефер, Герхард (2004), «Гравитомагнитные эффекты», Общая теория относительности и гравитации , 36 (10): 2223–2235, arXiv : gr-qc/0407116 , Bibcode : 2004GReGr..36.2223S , doi : 10.1023/B:GERG. 0000046180.97877.32 , S2CID   14255129
• Шедель, Р.; Отт, Т.; Гензель, Р.; Эккарт, А.; Муавад, Н.; Александр, Т. (2003), «Звездная динамика в центральной угловой секунде нашей Галактики», Astrophysical Journal , 596 (2): 1015–1034, arXiv : astro-ph/0306214 , Bibcode : 2003ApJ...596.1015S , doi : 10.1086/378122 , S2CID   17719367
• Шутц, Бернард Ф. (1985), Первый курс общей теории относительности , Cambridge University Press, ISBN  978-0-521-27703-7
• Шутц, Бернард Ф. (2003), Гравитация с нуля , Cambridge University Press, ISBN  978-0-521-45506-0
• Шварц, Джон Х. (2007), «Теория струн: прогресс и проблемы», Приложение Progress of Theoretical Physics , 170 : 214–226, arXiv : hep-th/0702219 , Bibcode : 2007PThPS.170..214S , doi : 10.1143 /PTPS.170.214 , S2CID   16762545
• Шварцшильд, Карл (1916а), «О гравитационном поле массовой точки согласно теории Эйнштейна», отчет о сессии. Пруссия. Акад. Д. Висс. : 189–196, Бибкод : 1916SPAW.......189S
• Шварцшильд, Карл (1916b), «О гравитационном поле сферы, сделанной из несжимаемой жидкости согласно теории Эйнштейна», отчет о сессии. Пруссия. Акад. Д. Висс. : 424–434, Бибкод : 1916skpa.conf..424S
• Зайдель, Эдвард (1998), «Численная теория относительности: к моделированию трехмерного слияния черных дыр», в Нарликаре, СП; Дадхич Н. (ред.), Гравитация и относительность: на рубеже тысячелетий (Материалы конференции GR-15, состоявшейся в IUCAA, Пуна, Индия, 16–21 декабря 1997 г.) , IUCAA, с. 6088, arXiv : gr-qc/9806088 , Bibcode : 1998gr.qc.....6088S , ISBN  978-81-900378-3-9
• Селяк, Урос; Залдарриага, Матиас (1997), «Признак гравитационных волн в поляризации микроволнового фона», Phys. Преподобный Летт. , 78 (11): 2054–2057, arXiv : astro-ph/9609169 , Bibcode : 1997PhRvL..78.2054S , doi : 10.1103/PhysRevLett.78.2054 , S2CID   30795875
• Шапиро, СС; Дэвис, Дж. Л.; Лебах, Делавэр; Грегори, Дж. С. (2004), «Измерение солнечного гравитационного отклонения радиоволн с использованием геодезических данных интерферометрии со сверхдлинной базой, 1979–1999», Phys. Преподобный Летт. , 92 (12): 121101, Bibcode : 2004PhRvL..92l1101S , doi : 10.1103/PhysRevLett.92.121101 , PMID   15089661
• Шапиро, Ирвин И. (1964), «Четвертый тест общей теории относительности», Phys. Преподобный Летт. , 13 (26): 789–791, Бибкод : 1964PhRvL..13..789S , doi : 10.1103/PhysRevLett.13.789
• Сингх, Саймон (2004), Большой взрыв: Происхождение Вселенной , Четвертая власть, Бибкод : 2004biba.book.....S , ISBN  978-0-00-715251-3
• Соркин, Рафаэль Д. (2005), «Причинные множества: дискретная гравитация», в Гомберофф, Андрес; Марольф, Дональд (ред.), Лекции по квантовой гравитации , Springer, стр. 9009, arXiv : gr-qc/0309009 , Bibcode : 2003gr.qc.....9009S , ISBN  978-0-387-23995-8
• Соркин, Рафаэль Д. (1997), «Развилка на пути к квантовой гравитации», Int. Дж. Теория. Физ. , 36 (12): 2759–2781, arXiv : gr-qc/9706002 , Bibcode : 1997IJTP...36.2759S , doi : 10.1007/BF02435709 , S2CID   4803804
• Спергель, Д.Н.; Верде, Л.; Пейрис, Х.В.; Комацу, Э.; Нолта, MR; Беннетт, CL; Халперн, М.; Хиншоу, Г.; и др. (2003), «Наблюдения первого года обучения с помощью микроволнового зонда анизотропии Уилкинсона (WMAP): определение космологических параметров», Astrophys. J. Приложение. Сер. , 148 (1): 175–194, arXiv : astro-ph/0302209 , Bibcode : 2003ApJS..148..175S , doi : 10.1086/377226 , S2CID   10794058
• Спергель, Д.Н.; Бин, Р .; Доре, О.; Нолта, MR; Беннетт, CL; Данкли, Дж.; Хиншоу, Г.; Ярошик, Н.; и др. (2007), «Результаты трехлетнего исследования микроволновой анизотропии Уилкинсона (WMAP): последствия для космологии», Приложение к Astrophysical Journal , 170 (2): 377–408, arXiv : astro-ph/0603449 , Bibcode : 2007ApJS..170.. 377S , doi : 10.1086/513700 , S2CID   1386346
• Спрингель, Волкер; Уайт, Саймон Д.М.; Дженкинс, Адриан; Френк, Карлос С.; Ёсида, Наоки; Гао, Лян; Наварро, Хулио; Такер, Роберт; и др. (2005), «Моделирование формирования, эволюции и кластеризации галактик и квазаров», Nature , 435 (7042): 629–636, arXiv : astro-ph/0504097 , Bibcode : 2005Natur.435..629S , doi : 10.1038 /nature03597 , PMID   15931216 , S2CID   4383030
• Стейрс, Ингрид Х. (2003), «Проверка общей теории относительности с помощью синхронизации пульсаров», Living Reviews in Relativity , 6 (1): 5, arXiv : astro-ph/0307536 , Bibcode : 2003LRR.....6... .5S , doi : 10.12942/lrr-2003-5 , PMC   5253800 , PMID   28163640
• Стефани, Х.; Крамер, Д.; МакКаллум, М.; Хоэнселерс, К.; Херлт, Э. (2003), Точные решения уравнений поля Эйнштейна (2-е изд.), Cambridge University Press, ISBN  978-0-521-46136-8
• Synge, JL (1972), Относительность: специальная теория , Издательство Северной Голландии, ISBN  978-0-7204-0064-9
• Сабадос, Ласло Б. (2004), «Квазилокальная энергия – импульс и угловой момент в ОТО», Living Reviews in Relativity , 7 (1): 4, Bibcode : 2004LRR.....7....4S , doi : 10.12942/lrr-2004-4 , PMC   5255888 , PMID   28179865
• Тейлор, Джозеф Х. (1994), «Двойные пульсары и релятивистская гравитация» , Rev. Mod. Физ. , 66 (3): 711–719, Bibcode : 1994RvMP...66..711T , doi : 10.1103/RevModPhys.66.711 , S2CID   120534048
• Тиманн, Томас (2007), «Петлевая квантовая гравитация: взгляд изнутри», Подходы к фундаментальной физике , Конспекты лекций по физике, том. 721, стр. 185–263, arXiv : hep-th/0608210 , Bibcode : 2007LNP...721..185T , doi : 10.1007/978-3-540-71117-9_10 , ISBN  978-3-540-71115-5 , S2CID   119572847
• Тиманн, Томас (2003). «Лекции по петлевой квантовой гравитации». У Доменико Дж. В. Джулини; Клаус Кифер; Клаус Леммерзал (ред.). Квантовая гравитация: от теории к экспериментальному поиску . Конспект лекций по физике. Том. 631. стр. 41–135. arXiv : gr-qc/0210094 . Бибкод : 2003ЛНП...631...41Т . дои : 10.1007/978-3-540-45230-0_3 . ISBN  978-3-540-40810-9 . S2CID   119151491 .
• Руководитель, Джерард ; Вельтман, Мартинус (1974), «Однопетлевые расхождения в теории гравитации», Annales de l'Institut Henri Poincaré A , 20 (1): 69, Бибкод : 1974AIHPA..20...69T
• Торн, Кип С. (1972), «Несферический гравитационный коллапс — краткий обзор», в Клаудер, Дж. (редактор), «Магия без магии» , WH Freeman, стр. 231–258.
• Торн, Кип С. (1994), Черные дыры и деформации времени: возмутительное наследие Эйнштейна , WW Norton & Company, ISBN  978-0-393-31276-8
• Торн, Кип С. (1995), «Гравитационное излучение», Астрофизика частиц и ядерная астрофизика и космология в следующем тысячелетии : 160, arXiv : gr-qc/9506086 , Bibcode : 1995pnac.conf..160T , ISBN  978-0-521-36853-7
• Торн, Кип (2003). «Искажение пространства-времени». В Г.В. Гиббонсе; ЭПС Шеллард; С. Дж. Рэнкин (ред.). Будущее теоретической физики и космологии: к 60-летию Стивена Хокинга . Издательство Кембриджского университета. ISBN  978-0-521-82081-3 .
• Таунсенд, Пол К. (1997). «Черные дыры (Конспект лекций)». arXiv : gr-qc/9707012 .
• Таунсенд, Пол К. (1996). «Четыре лекции по М-теории». Физика высоких энергий и космология . 13 : 385. arXiv : hep-th/9612121 . Бибкод : 1997hepcbconf..385T .
• Тращен, Дженни (2000), Быценко, А.; Уильямс, Ф. (ред.), «Введение в испарение черных дыр», Математические методы физики (Материалы Зимней школы Лондрины 1999 г.) , World Scientific: 180, arXiv : gr-qc/0010055 , Bibcode : 2000mmp.. конф..180T
• Траутман, Анджей (2006), «Теория Эйнштейна-Картана», в Франсуазе, Ж.-П.; Набер, ГЛ; Цоу, С.Т. (ред.), Энциклопедия математической физики, Vol. 2 , Elsevier, стр. 189–195, arXiv : gr-qc/0606062 , Bibcode : 2006gr.qc.....6062T
• Унру, WG (1976), «Заметки об испарении черных дыр», Phys. Rev. D , 14 (4): 870–892, Bibcode : 1976PhRvD..14..870U , doi : 10.1103/PhysRevD.14.870
• Вельтман, Мартинус (1975), «Квантовая теория гравитации», в Балиане, Роджере; Зинн-Жюстин, Жан (ред.), Методы теории поля - Летняя школа по теоретической физике в Ле Уше. , том. 77, Северная Голландия
• Уолд, Роберт М. (1975), «О создании частиц черными дырами» , Commun. Математика. Физ. , 45 (3): 9–34, Bibcode : 1975CMaPh..45....9W , doi : 10.1007/BF01609863 , S2CID   120950657
• Уолд, Роберт М. (1984), Общая теория относительности , Издательство Чикагского университета, ISBN  978-0-226-87033-5
• Уолд, Роберт М. (1994), Квантовая теория поля в искривленном пространстве-времени и термодинамика черных дыр , University of Chicago Press, Bibcode : 1994qftc.book.....W , ISBN  978-0-226-87027-4
• Уолд, Роберт М. (2001), «Термодинамика черных дыр», « Живые обзоры относительно относительности » , 4 (1): 6, arXiv : gr-qc/9912119 , Bibcode : 2001LRR.....4.... 6 Вт , doi : 10.12942/lrr-2001-6 , PMC   5253844 , PMID   28163633
• Уолш, Д.; Карсуэлл, РФ; Вейман, Р.Дж. (1979), «0957 + 561 A, B: двойные квазизвездные объекты или гравитационная линза?», Nature , 279 (5712): 381–4, Бибкод : 1979Natur.279..381W , doi : 10.1038/279381a0 , ПМИД   16068158 , С2КИД   2142707
• Вамбсгансс, Иоахим (1998), «Гравитационное линзирование в астрономии», Living Reviews in Relativity , 1 (1): 12, arXiv : astro-ph/9812021 , Bibcode : 1998LRR.....1...12W , doi : 10.12942/lrr-1998-12 , PMC   5567250 , PMID   28937183
• Вайнберг, Стивен (1972), Гравитация и космология: принципы и приложения общей теории относительности , Джон Уайли, ISBN  978-0-471-92567-5
• Вайнберг, Стивен (1995), Квантовая теория полей I: Основы , издательство Кембриджского университета, ISBN  978-0-521-55001-7
• Вайнберг, Стивен (1996), Квантовая теория полей II: современные приложения , издательство Кембриджского университета, ISBN  978-0-521-55002-4
• Вайнберг, Стивен (2000), Квантовая теория полей III: суперсимметрия , издательство Кембриджского университета, ISBN  978-0-521-66000-6
• Вайсберг, Джоэл М.; Тейлор, Джозеф Х. (2003), «Релятивистский двойной пульсар B1913+16» , в Бэйлсе, М.; Найс, ди-джей; Торсетт, С.Э. (ред.), Труды «Радиопульсаров», Ханья, Крит, август , 2002 , Серия конференций ASP
• Вайс, Ахим (2006), «Элементы прошлого: нуклеосинтез и наблюдение Большого взрыва» , Einstein Online , Институт гравитационной физики Макса Планка , заархивировано из оригинала 8 февраля 2007 г. , получено 24 февраля 2007 г.
• Уиллер, Джон А. (1990), Путешествие в гравитацию и пространство-время , Научно-американская библиотека, Сан-Франциско: WH Freeman, ISBN  978-0-7167-6034-4
• Уилл, Клиффорд М. (1993), Теория и эксперимент в гравитационной физике , Cambridge University Press, ISBN  978-0-521-43973-2
• Уилл, Клиффорд М. (2006), «Противостояние между общей теорией относительности и экспериментом», Living Reviews in Relativity , 9 (1): 3, arXiv : gr-qc/0510072 , Bibcode : 2006LRR.....9.. ..3W , doi : 10.12942/lrr-2006-3 , PMC   5256066 , PMID   28179873
• Цвибах, Бартон (2004), Первый курс теории струн , издательство Кембриджского университета, ISBN  978-0-521-83143-7

Дальнейшее чтение

Популярные книги

• Эйнштейн, А. (1916), Относительность: специальная и общая теория , Берлин, ISBN  978-3-528-06059-6 {{citation}}: CS1 maint: отсутствует местоположение издателя ( ссылка )
• Героч, Р. (1981), Общая теория относительности от А до Б , Чикаго: University of Chicago Press, ISBN.  978-0-226-28864-2
• Либер, Лилиан (2008), Теория относительности Эйнштейна: путешествие в четвертое измерение , Филадельфия: Paul Dry Books, Inc., ISBN  978-1-58988-044-3
• Шутц, Бернард Ф. (2001), «Гравитационное излучение», Мурдин, Пол (редактор), Энциклопедия астрономии и астрофизики , Публикация Института физики, ISBN  978-1-56159-268-5
• Торн, Кип ; Хокинг, Стивен (1994). Черные дыры и деформации времени: возмутительное наследие Эйнштейна . Нью-Йорк: WW Нортон. ISBN  0-393-03505-0 .
• Уолд, Роберт М. (1992), Пространство, время и гравитация: теория большого взрыва и черных дыр , Чикаго: University of Chicago Press, ISBN  978-0-226-87029-8
• Уилер, Джон ; Форд, Кеннет (1998), Геоны, черные дыры и квантовая пена: жизнь в физике , Нью-Йорк: WW Norton, ISBN  978-0-393-31991-0

Учебники для начального бакалавриата

• Каллахан, Джеймс Дж. (2000), Геометрия пространства-времени: введение в специальную и общую теорию относительности , Нью-Йорк: Springer, ISBN  978-0-387-98641-8
• Тейлор, Эдвин Ф.; Уиллер, Джон Арчибальд (2000), Исследование черных дыр: введение в общую теорию относительности , Аддисон Уэсли, ISBN  978-0-201-38423-9

Учебники для продвинутых студентов

• Ченг, Та-Пей (2005), Относительность, гравитация и космология: базовое введение , Оксфорд и Нью-Йорк: Oxford University Press, ISBN  978-0-19-852957-6
• Дирак, Поль (1996), Общая теория относительности , Princeton University Press, ISBN  978-0-691-01146-2
• Грон, О.; Хервик, С. (2007), Общая теория относительности Эйнштейна , Springer, ISBN  978-0-387-69199-2
• Хартл, Джеймс Б. (2003), Гравитация: введение в общую теорию относительности Эйнштейна , Сан-Франциско: Аддисон-Уэсли, ISBN  978-0-8053-8662-2
• Хьюстон, LP ; Тод, КП (1991), Введение в общую теорию относительности , Кембридж: Издательство Кембриджского университета, ISBN  978-0-521-33943-8
• д'Инверно, Рэй (1992), Знакомство с теорией относительности Эйнштейна , Оксфорд: Oxford University Press, ISBN  978-0-19-859686-8
• Людик, Гюнтер (2013). Эйнштейн в матричной форме (1-е изд.). Берлин: Шпрингер. ISBN  978-3-642-35797-8 .
• Мёллер, Кристиан (1955) [1952], Теория относительности , Oxford University Press, OCLC   7644624
• Мур, Томас А. (2012), Учебное пособие по общей теории относительности , Университетские научные книги, ISBN  978-1-891389-82-5
• Шутц, Б.Ф. (2009), Первый курс общей теории относительности (второе изд.), Cambridge University Press, ISBN  978-0-521-88705-2

Учебники для аспирантов

• Кэрролл, Шон М. (2004), Пространство-время и геометрия: введение в общую теорию относительности , Сан-Франциско: Аддисон-Уэсли, ISBN  978-0-8053-8732-2
• Грон, Эйвинд ; Хервик, Сигбьёрн (2007), Общая теория относительности Эйнштейна , Нью-Йорк: Springer, ISBN  978-0-387-69199-2
• Ландау Лев Д. ; Лифшиц, Евгений Ф. (1980), Классическая теория полей (4-е изд.) , Лондон: Баттерворт-Хайнеманн, ISBN  978-0-7506-2768-9
• Стефани, Ганс (1990), Общая теория относительности: введение в теорию гравитационного поля , Кембридж: Издательство Кембриджского университета, ISBN  978-0-521-37941-0
• Уилл, Клиффорд ; Пуассон, Эрик (2014). Гравитация: ньютоновская, постньютоновская, релятивистская . Издательство Кембриджского университета. ISBN  978-1-107-03286-6 .
• Чарльз В. Миснер ; Кип С. Торн ; Джон Арчибальд Уиллер (1973), Гравитация , WH Freeman, Princeton University Press, ISBN  0-7167-0344-0
• РК Сакс ; Х. Ву (1977), Общая теория относительности для математиков , Springer-Verlag, ISBN  1461299055
• Уолд, Роберт М. (1984). Общая теория относительности . Чикаго: Издательство Чикагского университета. ISBN  0-226-87032-4 . ОСЛК   10018614 .

Книги специалистов

• Хокинг, Стивен ; Эллис, Джордж (1975). Крупномасштабная структура пространства-времени . Издательство Кембриджского университета. ISBN  978-0-521-09906-6 .
• Пуассон, Эрик (2007). Инструментарий релятивиста: математика механики черных дыр . Издательство Кембриджского университета. ISBN  978-0-521-53780-3 .

Журнальные статьи

• Эйнштейн, Альберт (1916), «Основы общей теории относительности» , Annals of Physics , 49 (7): 769–822, Бибкод : 1916AnP...354..769E , doi : 10.1002/andp.19163540702 См. также английский перевод в Einstein Papers Project.
• Фланаган, Эанна Э.; Хьюз, Скотт А. (2005), «Основы теории гравитационных волн», New J. Phys. , 7 (1): 204, arXiv : gr-qc/0501041 , Bibcode : 2005NJPh....7..204F , doi : 10.1088/1367-2630/7/1/204
• Ландграф, М.; Гехлер, М.; Кембл, С. (2005), «Разработка миссии для LISA Pathfinder», класс. Квантовая гравитация. , 22 (10): S487–S492, arXiv : gr-qc/0411071 , Bibcode : 2005CQGra..22S.487L , doi : 10.1088/0264-9381/22/10/048 , S2CID   119476595
• Ньето, Майкл Мартин (2006), «В поисках понимания аномалии Пионера» (PDF) , Europhysical News , 37 (6): 30–34, arXiv : gr-qc/0702017 , Bibcode : 2006ENews..37f..30N , doi : 10.1051/epn:2006604 , в архиве (PDF) из оригинала 24 сентября 2015 г.
• Шапиро, II ; Петтенгилл, Гордон; Эш, Майкл; Стоун, Мелвин; Смит, Уильям; Ингаллс, Ричард; Брокельман, Ричард (1968), «Четвертый тест общей теории относительности: предварительные результаты», Phys. Преподобный Летт. , 20 (22): 1265–1269, Бибкод : 1968PhRvL..20.1265S , doi : 10.1103/PhysRevLett.20.1265
• Валтонен, МЮ; Лехто, HJ; Нильссон, К.; Хайдт, Дж.; Такало, Лоу; Силланпяя, А.; Уилфорт, К.; Киджер, М.; и др. (2008), «Массивная двойная система черных дыр в OJ 287 и тест общей теории относительности», Nature , 452 (7189): 851–853, arXiv : 0809.1280 , Bibcode : 2008Natur.452..851V , doi : 10.1038 /nature06896 , PMID   18421348 , S2CID   4412396

Внешние ссылки

• Эйнштейн в Интернете. Архивировано 1 июня 2014 г. в Wayback Machine . Статьи по различным аспектам релятивистской физики для широкой аудитории; организован Институтом гравитационной физики Макса Планка.
• Домашняя страница GEO600 , официальный сайт проекта GEO600.
• Лаборатория ЛИГО
• NCSA Spacetime Wrinkles - создано группой численной теории относительности NCSA и содержит элементарное введение в общую теорию относительности.

• Курсы
• Лекции
• Учебники

• Общая теория относительности Эйнштейна на YouTube (лекция Леонарда Зюскинда, записанная 22 сентября 2008 года в Стэнфордском университете ).
• Серия лекций по общей теории относительности, прочитанных в 2006 г. в Институте Анри Пуанкаре (вводный/продвинутый уровень).
• Уроки общей теории относительности Джона Баэза .
• Браун, Кевин. «Размышления об относительности» . Mathpages.com . Архивировано из оригинала 18 декабря 2015 года . Проверено 29 мая 2005 г.
• Кэрролл, Шон М. (1997). «Конспекты лекций по общей теории относительности». arXiv : gr-qc/9712019 .
• Мавр, Рафи. «Понимание общей теории относительности» . Проверено 11 июля 2006 г.
• Ванер, Стефан. «Введение в дифференциальную геометрию и общую теорию относительности» . Проверено 5 апреля 2015 г.
• Фейнмановские лекции по физике Vol. II гл. 42: Искривленное пространство