Теория игр

Теория игр — это изучение математических моделей стратегических взаимодействий. ^[1] Он находит применение во многих областях социальных наук и широко используется в экономике , логике , системных науках и информатике . ^[2] двух человек Первоначально теория игр рассматривала игры с нулевой суммой для , в которых выигрыши или проигрыши одного участника точно уравновешиваются проигрышами и выигрышами другого участника. В 1950-х годах оно было распространено на изучение игр с ненулевой суммой и в конечном итоге было применено к широкому спектру поведенческих отношений . Сейчас это общий термин для науки о рациональном принятии решений у людей, животных и компьютеров.

Современная теория игр началась с идеи равновесия смешанных стратегий в играх двух лиц с нулевой суммой и ее доказательства Джоном фон Нейманом . В оригинальном доказательстве фон Неймана использовалась теорема Брауэра о неподвижной точке о непрерывных отображениях в компактные выпуклые множества , которая стала стандартным методом в теории игр и математической экономике . За его статьей последовала «Теория игр и экономического поведения» (1944), написанная в соавторстве с Оскаром Моргенштерном , в которой рассматривались совместные игры нескольких игроков. ^[3] Во втором издании представлена аксиоматическая теория ожидаемой полезности , которая позволила математическим статистикам и экономистам рассматривать процесс принятия решений в условиях неопределенности. ^[4]

Теория игр получила широкое развитие в 1950-х годах и была открыто применена к эволюции в 1970-х годах, хотя аналогичные разработки начались, по крайней мере, с 1930-х годов. Теория игр получила широкое признание как важный инструмент во многих областях. Джон Мейнард Смит был удостоен премии Крафорда за применение эволюционной теории игр в 1999 году, а пятнадцать теоретиков игр получили Нобелевскую премию по экономике по состоянию на 2020 год, в том числе совсем недавно Пол Милгром и Роберт Б. Уилсон .

История

Теоретико-игровая мысль

Теоретико-игровая стратегия в письменной истории восходит, по крайней мере, к Сунь Цзы руководству по военной стратегии . ^[5]^[6] В «Искусстве войны » он писал

Зная другого и зная себя, В ста боях никакой опасности,
Не зная другого и зная себя, Одна победа за одно поражение,
Не зная другого и не зная себя, В каждой битве верный проигрыш.
— Сунь Цзы

Математическое происхождение

Дискуссии по математике игр начались задолго до появления современной математической теории игр. Liber Работа Кардано de ludo aleae ( «Книга об азартных играх »), написанная около 1564 года, но опубликованная посмертно в 1663 году, обрисовывает некоторые основные идеи азартных игр. В 1650-х годах Паскаль и Гюйгенс разработали концепцию ожидания на основе рассуждений о структуре азартных игр. Паскаль выступал за равное разделение, когда шансы равны, в то время как Гюйгенс расширил этот аргумент, рассматривая стратегии для игрока, который может сделать любую ставку с любым противником, при условии, что ее условия равны. ^[7] Позже Гюйгенс опубликовал свое исчисление азартных игр под названием Deatiociniis in ludo aleæ ( «О рассуждениях в азартных играх ») в 1657 году.

В 1713 году в письме, приписываемом Чарльзу Уолдегрейву, активному якобиту и дяде британского дипломата Джеймса Уолдегрейва , анализировалась игра под названием « ле ее ». ^[8]^[9] Уолдегрейв предложил минимаксное решение смешанной стратегии для версии карточной игры для двух человек, и эта проблема теперь известна как проблема Уолдегрейва . В 1838 году Антуан Огюстен Курно рассмотрел дуополию и представил решение, которое представляет собой равновесие Нэша игры, в своих исследованиях по математическим принципам теории богатства ( Recherches sur les principes mathématiques de la theorie des richesses ).

В 1913 году Эрнст Цермело опубликовал Über eine Anwendung der Mengenlehre auf die Theorie des Schachspiels (« О применении теории множеств к теории игры в шахматы» ), в которой доказал, что оптимальная шахматная стратегия строго определена . Это открыло путь к более общим теоремам. ^[10]

В 1938 году датский экономист-математик Фредерик Цойтен доказал, что математическая модель имеет выигрышную стратегию, используя теорему Брауэра о фиксированной точке . ^[11] В своей книге 1938 года «Приложения к играм Хасара» и более ранних заметках Эмиль Борель доказал теорему о минимаксе для матричных игр двух лиц с нулевой суммой только тогда, когда матрица выигрышей симметрична, и предоставил решение нетривиальной бесконечной игры (известной на английском языке как игра Blotto ). Борель выдвинул гипотезу об отсутствии равновесия со смешанными стратегиями в конечных играх двух лиц с нулевой суммой , гипотеза, ложность которой была доказана фон Нейманом.

Рождение и раннее развитие

Теория игр стала уникальной областью науки, когда Джон фон Нейман опубликовал в 1928 году статью «Теория стратегических игр» . ^[12]^[13] В оригинальном доказательстве фон Неймана использовалась теорема Брауэра о неподвижной точке о непрерывных отображениях в компактные выпуклые множества , которая стала стандартным методом в теории игр и математической экономике . Работа фон Неймана в области теории игр завершилась в 1944 году его книгой «Теория игр и экономического поведения» , написанной в соавторстве с Оскаром Моргенштерном . ^[14] Во втором издании этой книги представлена аксиоматическая теория полезности , которая реинкарнировала Даниэля Бернулли старую теорию полезности (денег) в качестве независимой дисциплины. Эта основополагающая работа содержит метод поиска взаимно непротиворечивых решений для игр двух лиц с нулевой суммой. Последующая работа была сосредоточена в первую очередь на теории кооперативных игр , которая анализирует оптимальные стратегии для групп людей, предполагая, что они могут обеспечить соблюдение соглашений между собой о правильных стратегиях. ^[15]

В 1950 году появилось первое математическое обсуждение дилеммы заключённого провели эксперимент , и известные математики Меррил М. Флад и Мелвин Дрешер в рамках RAND исследований теории игр, проводимых корпорацией . РЭНД продолжил исследования из-за возможного применения их в глобальной ядерной стратегии . ^[16] Примерно в это же время Джон Нэш разработал критерий взаимной согласованности стратегий игроков, известный как равновесие Нэша , применимый к более широкому разнообразию игр, чем критерий, предложенный фон Нейманом и Моргенштерном. с n игроками и ненулевой суммой (а не только двумя игроками с нулевой суммой) Нэш доказал, что каждая конечная некооперативная игра имеет то, что сейчас известно как равновесие Нэша в смешанных стратегиях.

Теория игр пережила бурную деятельность в 1950-х годах, в ходе которой были разработаны концепции ядра , игры развернутой формы , фиктивной игры , повторяющихся игр и ценности Шепли . В 1950-е годы также появились первые применения теории игр в философии и политической науке .

Призовые достижения

В 1965 году Рейнхард Зельтен представил свою концепцию решения , идеальных равновесий подыгр которая еще больше уточнила равновесие Нэша. Позже он представит совершенство дрожащей руки и . В 1994 году Нэш, Селтен и Харсаньи стали лауреатами Нобелевской премии по экономике за вклад в теорию экономических игр.

В 1970-е годы теория игр широко применялась в биологии , во многом благодаря работам Джона Мейнарда Смита и его эволюционно стабильной стратегии . Кроме того, концепции коррелированного равновесия , совершенства дрожащей руки и общеизвестных знаний ^[а] были представлены и проанализированы.

В 1994 году Джон Нэш был удостоен Нобелевской премии по экономике за вклад в теорию игр. Самым известным вкладом Нэша в теорию игр является концепция равновесия Нэша, которая является концепцией решения для некооперативных игр . Равновесие Нэша — это набор стратегий, по одной для каждого игрока, при котором ни один игрок не может улучшить свой выигрыш, изменив в одностороннем порядке свою стратегию.

В 2005 году теоретики игр Томас Шеллинг и Роберт Ауманн последовали за Нэшем, Селтеном и Харсаньи в качестве лауреатов Нобелевской премии. Шеллинг работал над динамическими моделями, ранними примерами эволюционной теории игр . Ауманн внес больший вклад в школу равновесия, введя огрубление равновесия и коррелированные равновесия, а также разработав обширный формальный анализ предположения об общем знании и его последствий.

В 2007 году Леонид Гурвич , Эрик Маскин и Роджер Майерсон были удостоены Нобелевской премии по экономике «за заложение основ теории проектирования механизмов ». Вклад Майерсона включает понятие правильного равновесия и важный дипломный труд: «Теория игр, анализ конфликта» . ^[1] Гурвич ввел и формализовал концепцию совместимости стимулов .

В 2012 году Элвин Э. Рот и Ллойд С. Шепли были удостоены Нобелевской премии по экономике «за теорию стабильного распределения и практику проектирования рынка». В 2014 году Нобелевская премия досталась теоретику игр Жану Тиролю .

Различные типы игр

Кооперативный/некооперативный

Игра является кооперативной , если игроки могут формировать обязательные обязательства, принудительно реализуемые извне (например, посредством договорного права ). Игра считается некооперативной , если игроки не могут создавать альянсы или если все соглашения должны быть самодостаточными (например, посредством реальных угроз ). ^[17]

Кооперативные игры часто анализируются в рамках теории кооперативных игр , которая фокусируется на прогнозировании того, какие коалиции сформируются, совместные действия, которые предпримут группы, и полученные в результате коллективные выплаты. Она отличается от теории некооперативных игр , которая фокусируется на прогнозировании действий и выигрышей отдельных игроков путем анализа равновесия Нэша . ^[18]^[19]

Теория кооперативных игр обеспечивает подход высокого уровня, поскольку она описывает только структуру и выигрыши коалиций, тогда как некооперативная теория игр также рассматривает, как стратегическое взаимодействие повлияет на распределение выигрышей. Поскольку некооперативная теория игр является более общей, кооперативные игры можно анализировать с помощью подхода некооперативной теории игр (обратное утверждение неверно) при условии, что сделаны достаточные предположения, чтобы охватить все возможные стратегии, доступные игрокам, из-за возможности внешнего обеспечения сотрудничества.

Симметричный/асимметричный

	И	Ф
И	1, 2	0, 0
Ф	0, 0	1, 2
Асимметричная игра

Симметричная игра — это игра, в которой каждый игрок получает одинаковый выигрыш, делая один и тот же выбор. Другими словами, личность игрока не меняет исход игры с другим игроком. ^[20] Многие из широко изучаемых игр 2х2 симметричны. Стандартные представления о курице , дилемме заключенного и охоте на оленя — все это симметричные игры.

Наиболее часто изучаемыми асимметричными играми являются игры, в которых у обоих игроков нет одинаковых наборов стратегий. Например, игра «Ультиматум» , как и игра «Диктатор», имеют разные стратегии для каждого игрока. Однако игра может иметь одинаковые стратегии для обоих игроков, но быть асимметричной. Например, игра, изображенная на рисунке в этом разделе, асимметрична, несмотря на идентичные наборы стратегий для обоих игроков.

Нулевая сумма/ненулевая сумма

	А	Б
А	–1, 1	3, −3
Б	0, 0	–2, 2
Игра с нулевой суммой

Игры с нулевой суммой (в более общем смысле, игры с постоянной суммой) — это игры, в которых выбор игроков не может ни увеличить, ни уменьшить доступные ресурсы. В играх с нулевой суммой общая выгода достается всем игрокам в игре для каждой комбинации стратегий и всегда равна нулю (более неформально, игрок получает выгоду только за равный счет других). ^[21] Покер является примером игры с нулевой суммой (игнорируя возможность сокращения казино), поскольку каждый выигрывает ровно столько, сколько проигрывают его оппоненты. Другие игры с нулевой суммой включают в себя сопоставление монет и большинство классических настольных игр, включая го и шахматы .

Многие игры, изучаемые теоретиками игр (в том числе знаменитая дилемма заключенного), являются играми с ненулевой суммой, поскольку конечный результат больше или меньше нуля. Неофициально в играх с ненулевой суммой выигрыш одного игрока не обязательно соответствует проигрышу другого.

Более того, игры с постоянной суммой соответствуют таким видам деятельности, как воровство и азартные игры, но не фундаментальной экономической ситуации, в которой существуют потенциальные выгоды от торговли . Любую игру с постоянной суммой можно превратить в игру (возможно, асимметричную) с нулевой суммой, добавив фиктивного игрока (часто называемого «доской»), проигрыши которого компенсируют чистый выигрыш игроков.

Одновременный/последовательный

Одновременные игры — это игры, в которых оба игрока движутся одновременно, или вместо этого более поздние игроки не знают о действиях предыдущих игроков (что делает их фактически одновременными). Последовательные игры (или динамические игры) — это игры, в которых игроки не принимают решения одновременно, а более ранние действия игрока влияют на результат и решения других игроков. ^[22] Это не обязательно должна быть точная информация о каждом действии предыдущих игроков; это может быть очень мало знаний. Например, игрок может знать, что предыдущий игрок не выполнил одно конкретное действие, но при этом он не знает, какое из других доступных действий фактически выполнил первый игрок.

Разница между одновременными и последовательными играми отражена в различных представлениях, обсуждавшихся выше. Часто нормальная форма используется для представления одновременных игр, а развернутая форма — для представления последовательных. Преобразование развернутой формы в нормальную является одним из способов, означающим, что одной и той же нормальной форме соответствует несколько игр с развернутой формой. Следовательно, понятия равновесия для одновременных игр недостаточны для рассуждений о последовательных играх; см. совершенство субигры .

Вкратце, различия между последовательными и одновременными играми заключаются в следующем:

	Последовательный	Одновременный
Обычно обозначается	Деревья решений	Матрицы выплат
Предварительные знания хода противника?	Да	Нет
Ось времени?	Да	Нет
Также известен как	Игра развернутой формы Обширная игра	Стратегическая игра Стратегическая игра

Совершенная информация и несовершенная информация

Важную подгруппу последовательных игр составляют игры с полной информацией. Игра с полной информацией означает, что все игроки при каждом своем ходе знают предысторию игры и ходы, сделанные ранее всеми остальными игроками. Игра с несовершенной информацией ведется, когда игроки не знают всех ходов, уже сделанных противником, например игра с одновременными ходами. ^[23] Примеры игр с идеальной информацией включают крестики-нолики , шашки , шахматы и го . ^[24]^[25]^[26]

Многие карточные игры представляют собой игры с несовершенной информацией, например покер и бридж . ^[27] Совершенную информацию часто путают с полной информацией , которая представляет собой аналогичную концепцию, относящуюся к общему знанию последовательности действий, стратегий и выигрышей каждого игрока на протяжении всего игрового процесса. ^[28] Полная информация требует, чтобы каждый игрок знал стратегии и выигрыши, доступные другим игрокам, но не обязательно предпринятые действия, тогда как идеальная информация — это знание всех аспектов игры и игроков. ^[29] Однако игры с неполной информацией можно свести к играм с несовершенной информацией путем введения « естественных ходов ». ^[30]

Байесовская игра

Одно из предположений равновесия Нэша состоит в том, что каждый игрок имеет правильные убеждения о действиях других игроков. Однако в теории игр существует множество ситуаций, когда участники не до конца понимают характеристики своих противников. Участники переговоров могут не знать, как их оппонент оценивает объект переговоров, компании могут не знать о функциях издержек своего оппонента, участники боевых действий могут не знать о сильных сторонах своего оппонента, а присяжные могут не знать о том, как их коллеги интерпретируют доказательства в суде. В некоторых случаях участники могут хорошо знать характер своего оппонента, но могут не знать, насколько хорошо противник знает свой собственный характер. ^[31]

Байесовская игра означает стратегическую игру с неполной информацией. В стратегической игре лицами, принимающими решения, являются игроки, и у каждого игрока есть группа действий. Основной частью несовершенной информационной спецификации является набор состояний. Каждое состояние полностью описывает набор характеристик, важных для игрока, таких как его предпочтения и подробности о нем. Должно быть состояние для каждого набора функций, которые, по мнению некоторых игроков, могут существовать. ^[32]

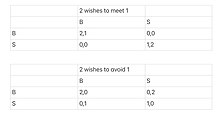
Например, когда Игрок 1 не уверен, предпочтет ли Игрок 2 встречаться с ней или уйти от нее, в то время как Игрок 2, как и раньше, понимает предпочтения Игрока 1. Точнее, предположим, что Игрок 1 считает, что Игрок 2 хочет встречаться с ней с вероятностью 1/2 и уйти от нее с вероятностью 1/2 (эта оценка, вероятно, основана на опыте Игрока 1: она сталкивается с игроками, которые хотят встречаться с ней половину времени в таком случае и игроками, которые хотят избегать ее половину времени). Из-за задействованной вероятности анализ этой ситуации требует понимания предпочтения игрока в отношении ничьей, хотя людей интересует только чистое стратегическое равновесие.

Комбинаторные игры

Игры, в которых сложность поиска оптимальной стратегии обусловлена множественностью возможных ходов, называются комбинаторными играми. Примеры включают шахматы и Го . Игры, в которых используется несовершенная информация , также могут иметь сильный комбинаторный характер, например нарды . Не существует единой теории комбинаторных элементов в играх. Однако существуют математические инструменты, которые могут решить некоторые частные проблемы и ответить на некоторые общие вопросы. ^[33]

Игры с совершенной информацией изучались в комбинаторной теории игр , которая разработала новые представления, например, сюрреалистические числа , а также комбинаторные и алгебраические (а иногда и неконструктивные ) методы доказательства для решения игр определенных типов, включая «зацикленные» игры, которые может привести к бесконечно длинным последовательностям ходов. Эти методы относятся к играм с более высокой комбинаторной сложностью, чем те, которые обычно рассматриваются в традиционной (или «экономической») теории игр. ^[34]^[35] Типичная игра, решенная таким образом, — Hex . Смежной областью исследований, основанной на теории сложности вычислений , является сложность игр , которая занимается оценкой вычислительной сложности поиска оптимальных стратегий. ^[36]

Исследования в области искусственного интеллекта касаются как совершенных, так и несовершенных информационных игр, имеющих очень сложную комбинаторную структуру (например, шахматы, го или нарды), для которых не найдено доказуемых оптимальных стратегий. Практические решения включают в себя вычислительную эвристику, такую как альфа-бета-обрезка или использование искусственных нейронных сетей, обученных с помощью обучения с подкреплением , что делает игры более удобными для компьютерной практики. ^[33]^[37]

Дискретные и непрерывные игры

Большая часть теории игр посвящена конечным дискретным играм с конечным числом игроков, ходов, событий, результатов и т. д. Однако многие концепции можно расширить. Непрерывные игры позволяют игрокам выбирать стратегию из набора непрерывных стратегий. Например, конкуренция по Курно обычно моделируется, когда стратегии игроков представляют собой любые неотрицательные величины, в том числе дробные.

Дифференциальные игры

Дифференциальные игры, такие как игра с непрерывным преследованием и уклонением, представляют собой непрерывные игры, в которых эволюция переменных состояния игроков управляется дифференциальными уравнениями . Проблема поиска оптимальной стратегии в дифференциальной игре тесно связана с теорией оптимального управления . В частности, существует два типа стратегий: стратегии разомкнутого цикла находятся с использованием принципа максимума Понтрягина , а стратегии замкнутого цикла находятся с использованием метода динамического программирования Беллмана .

Частным случаем дифференциальных игр являются игры со случайным временным горизонтом . ^[38] В таких играх конечное время является случайной величиной с заданной функцией распределения вероятностей . Следовательно, игроки максимизируют математическое ожидание функции стоимости. Показано, что модифицированную задачу оптимизации можно переформулировать как дифференциальную игру со скидкой на бесконечном интервале времени.

Эволюционная теория игр

Эволюционная теория игр изучает игроков, которые со временем корректируют свои стратегии в соответствии с правилами, которые не обязательно являются рациональными или дальновидными. ^[39] В общем, эволюция стратегий во времени в соответствии с такими правилами моделируется как цепь Маркова с переменной состояния, такой как текущий профиль стратегии или то, как игра велась в недавнем прошлом. Такие правила могут включать имитацию, оптимизацию или выживание наиболее приспособленных.

В биологии такие модели могут представлять собой эволюцию , в которой потомство перенимает стратегии своих родителей, а родители, которые применяют более успешные стратегии (т. е. соответствующие более высоким выигрышам), имеют большее количество потомков. В социальных науках такие модели обычно представляют собой стратегическую корректировку игроков, которые играют в игру много раз в течение своей жизни и сознательно или неосознанно время от времени корректируют свои стратегии. ^[40]

Стохастические результаты (и связь с другими областями)

Задачи индивидуального решения со случайными результатами иногда называют «играми для одного игрока». Их можно моделировать с использованием аналогичных инструментов в рамках смежных дисциплин теории принятия решений , исследования операций и областей искусственного интеллекта , в частности планирования ИИ (с неопределенностью) и многоагентных систем . Хотя эти области могут иметь разные мотиваторы, применяемая математика по существу одинакова, например, использование марковских процессов принятия решений (MDP). ^[41]

Стохастические результаты также можно смоделировать с точки зрения теории игр, добавив случайно действующего игрока, который делает «случайные ходы» (« ходы по своей природе »). ^[42] Этот игрок обычно не считается третьим игроком в игре для двух игроков, а просто служит для обеспечения броска кубиков там, где этого требует игра.

Для некоторых проблем разные подходы к моделированию стохастических результатов могут привести к разным решениям. Например, разница в подходе между MDP и минимаксным решением заключается в том, что последнее рассматривает наихудший случай из набора состязательных ходов, а не рассуждает в ожидании об этих ходах с учетом фиксированного распределения вероятностей. Минимаксный подход может быть выгоден там, где стохастические модели неопределенности недоступны, но он также может привести к переоценке крайне маловероятных (но дорогостоящих) событий, резко влияя на стратегию в таких сценариях, если предполагается, что противник может заставить такое событие произойти. ^[43] ( см. в «Теории черного лебедя» Подробнее об этом виде проблем моделирования, особенно в том, что касается прогнозирования и ограничения убытков в инвестиционно-банковской сфере, .)

Также изучались общие модели, включающие все элементы стохастических исходов, противников и частичную или зашумленную наблюдаемость (ходов других игроков). « Золотым стандартом » считается частично наблюдаемая стохастическая игра (POSG), но в представлении POSG вычислительно осуществимо лишь несколько реалистичных задач. ^[43]

Метаигры

Это игры, игра в которых представляет собой разработку правил другой игры, целевой или предметной игры. Метаигры стремятся максимизировать полезность разработанного набора правил. Теория метаигр связана с теорией проектирования механизмов .

Термин «анализ метаигры» также используется для обозначения практического подхода, разработанного Найджелом Ховардом. ^[44] при этом ситуация оформляется как стратегическая игра, в которой заинтересованные стороны пытаются реализовать свои цели посредством доступных им вариантов. Последующие события привели к формулировке анализа конфронтации .

Теория игр среднего поля

Теория игр среднего поля — это исследование принятия стратегических решений в очень больших популяциях небольших взаимодействующих агентов. Этот класс проблем рассматривался в экономической литературе Бояном Йовановичем и Робертом В. Розенталем , в инженерной литературе Питером Э. Кейнсом и математиками Пьером-Луи Лионсом и Жаном-Мишелем Ласри.

Представление игр

Игры, изучаемые в теории игр, представляют собой четко определенные математические объекты. Для полного определения игра должна определять следующие элементы: игроки игры, информация и действия, доступные каждому игроку в каждой точке принятия решения, а также выигрыши для каждого результата. (Эрик Расмусен называет эти четыре «необходимых элемента» аббревиатурой «PAPI».) ^[45]^[46]^[47]^[48] Теоретик игр обычно использует эти элементы вместе с концепцией решения по своему выбору, чтобы вывести набор равновесных стратегий для каждого игрока, так что при использовании этих стратегий ни один игрок не сможет получить прибыль, отклонившись в одностороннем порядке от своей стратегии. Эти стратегии равновесия определяют равновесие в игре — стабильное состояние, в котором происходит либо один результат, либо набор результатов с известной вероятностью.

Большинство кооперативных игр представлены в характеристической функциональной форме, тогда как экстенсивная и нормальная формы используются для определения некооперативных игр.

Расширенная форма

Развернутая форма может быть использована для формализации игр с временной последовательностью ходов. Игры обширной формы можно визуализировать с помощью деревьев игр (как показано здесь). Здесь каждая вершина (или узел) представляет собой точку выбора для игрока. Игрок определяется числом, указанным в вершине. Линии, выходящие из вершины, представляют собой возможное действие этого игрока. Выплаты указаны в нижней части дерева. Развернутую форму можно рассматривать как многопользовательское обобщение дерева решений . ^[49] Для решения любой игры расширенной формы обратную индукцию необходимо использовать . Он включает в себя движение назад вверх по дереву игры, чтобы определить, что бы сделал рациональный игрок в последней вершине дерева, что сделал бы игрок, сделавший предыдущий ход, учитывая, что игрок, сделавший последний ход, является рациональным, и так далее до первого шага. вершина дерева достигнута. ^[50]

Изображенная игра состоит из двух игроков. В соответствии со структурой этой конкретной игры (т. е. с последовательным принятием решений и точной информацией), Игрок 1 «ходит» первым, выбирая либо F , либо U (честно или несправедливо). Далее в последовательности Игрок 2 , который теперь наблюдает 1 за ходом Игрока , может выбрать ход A или R (принять или отклонить). Как только Игрок 2 сделал свой выбор, игра считается завершенной, и каждый игрок получает соответствующий выигрыш, представленный на изображении в виде двух чисел, где первое число представляет выигрыш Игрока 1, а второе число представляет выигрыш Игрока 2. Предположим, что игрок 1 выбирает U , а затем игрок 2 выбирает A : тогда игрок 1 получает выигрыш в размере «восемь» (что в реальных условиях можно интерпретировать по-разному, самый простой из которых - в терминах денег, но может означать разные вещи). например, восемь дней отпуска или восемь завоеванных стран или даже еще восемь возможностей сыграть в ту же игру против других игроков), и Игрок 2 получает выигрыш «два».

Расширенная форма также может охватывать игры с одновременными ходами и игры с несовершенной информацией. Для этого либо пунктирная линия соединяет разные вершины, чтобы представить их как часть одного и того же набора информации (т. е. игроки не знают, в какой точке они находятся), либо вокруг них рисуется замкнутая линия. (См. пример в разделе несовершенной информации .)

Нормальная форма

	Игрок 2 выбирает Левый	Игрок 2 выбирает правильно
Игрок 1 выбирает Вверх	4 , 3	–1 , –1
Игрок 1 выбирает Вниз	0 , 0	3 , 4
Нормальная форма или матрица выигрышей игры с двумя игроками и двумя стратегиями.

Обычная игра (или стратегическая форма) обычно представляет собой матрицу , показывающую игроков, стратегии и выигрыши (см. пример справа). В более общем смысле ее можно представить любой функцией, которая связывает выигрыш каждого игрока со всеми возможными комбинациями действий. В сопровождающем примере есть два игрока; один выбирает строку, а другой выбирает столбец. У каждого игрока есть две стратегии, которые определяются количеством строк и количеством столбцов. Выплаты предусмотрены внутри. Первое число — это выигрыш, полученный игроком ряда (Игрок 1 в нашем примере); второй — это выигрыш для игрока столбца (Игрок 2 в нашем примере). Предположим, что Игрок 1 играет «Вверх» , а Игрок 2 — «Влево» . Тогда игрок 1 получает выигрыш 4, а игрок 2 — 3.

Когда игра представлена в нормальной форме, предполагается, что каждый игрок действует одновременно или, по крайней мере, не знает действий другого. Если игроки имеют некоторую информацию о выборе других игроков, игра обычно представлена в развернутой форме.

Каждая игра в расширенной форме имеет эквивалентную игру в нормальной форме, однако преобразование в нормальную форму может привести к экспоненциальному увеличению размера представления, что делает его непрактичным с вычислительной точки зрения. ^[51]

Характеристическая форма функции

В теории кооперативных игр характеристическая функция перечисляет выигрыш каждой коалиции. Истоком этой формулировки является книга Джона фон Неймана и Оскара Моргенштерна. ^{[ нужна ссылка ]}

Формально характеристическая функция — это функция $v:2^{N}\to \mathbb {R}$ ^[52] от множества всех возможных коалиций игроков до множества платежей, а также удовлетворяет $v(\emptyset )=0$ . Функция описывает, какой коллективный выигрыш может получить группа игроков, сформировав коалицию.

Альтернативные представления игры

Альтернативные формы представления игр используются для некоторых подклассов игр или адаптированы к потребностям междисциплинарных исследований. ^[53] В дополнение к классическим представлениям игры, некоторые альтернативные представления также кодируют аспекты, связанные со временем.

Имя	Год	Означает	Тип игр	Время
Игра с пробками ^[54]	1973	функции	подмножество игр для n человек, одновременные ходы	Нет
Последовательная форма ^[55]	1994	матрицы	Игры для двоих с несовершенной информацией	Нет
Игры на время ^[56]^[57]	1994	функции	игры для двоих	Да
Гала ^[58]	1997	логика	игры с несовершенной информацией для n человек	Нет
Графические игры ^[59]^[60]	2001	графики, функции	игры для n человек, одновременные ходы	Нет
Игры с локальным эффектом ^[61]	2003	функции	подмножество игр для n человек, одновременные ходы	Нет
ВКЛ ^[62]	2005	логика	детерминированные игры для n человек, одновременные ходы	Нет
Игры Сети Петри ^[63]	2006	сеть Петри	детерминированные игры для n человек, одновременные ходы	Нет
Непрерывные игры ^[64]	2007	функции	подмножество игр для двоих с несовершенной информацией	Да
ПНСИ ^[65]^[66]	2008	сеть Петри	игры с несовершенной информацией для n человек	Да
Графические игры действия ^[67]	2012	графики, функции	игры для n человек, одновременные ходы	Нет

Общее и прикладное использование

Как метод прикладной математики теория игр использовалась для изучения широкого спектра поведения человека и животных. Первоначально он был разработан в экономике для понимания большого набора экономических моделей поведения, включая поведение фирм, рынков и потребителей. Впервые теоретико-игровой анализ был использован Антуаном Огюстеном Курно в 1838 году, когда он решил дуополию Курно . Использование теории игр в социальных науках расширилось, а теория игр также стала применяться к политическому, социологическому и психологическому поведению. ^[68]

до двадцатого века, Хотя натуралисты такие как Чарльз Дарвин, делали утверждения, относящиеся к теории игр, использование теоретико-игрового анализа в биологии началось с Рональдом Фишером исследований поведения животных, проведенных в 1930-х годах. Эта работа предшествовала названию «теория игр», но она имеет много общих черт с этой областью. Развитие экономики было позже применено к биологии главным образом Джоном Мейнардом Смитом в его книге 1982 года «Эволюция и теория игр» . ^[69]

Помимо описания, прогнозирования и объяснения поведения, теория игр также использовалась для разработки теорий этического или нормативного поведения и для предписания такого поведения. ^[70] В экономике и философии ученые применяли теорию игр, чтобы помочь понять хорошее или правильное поведение. Теоретико-игровые подходы также были предложены в философии языка и философии науки . ^[71] Теоретико-игровые аргументы такого типа можно найти еще у Платона . ^[72] Альтернативная версия теории игр, называемая химической теорией игр , представляет выбор игрока в виде метафорических молекул химических реагентов, называемых «нолекулы». ^[73] Затем химическая теория игр рассчитывает результаты как равновесные решения системы химических реакций.

Описание и моделирование

Основное применение теории игр — описание и моделирование поведения человеческой популяции. ^{[ нужна ссылка ]} Некоторый ^{[ ВОЗ? ]} Ученые полагают, что, находя равновесие в играх, они могут предсказать, как поведет себя реальная человеческая популяция, столкнувшись с ситуациями, аналогичными изучаемой игре. Этот конкретный взгляд на теорию игр подвергся критике. Утверждается, что предположения, сделанные теоретиками игр, часто нарушаются при применении к реальным ситуациям. Теоретики игр обычно предполагают, что игроки действуют рационально, но на практике человеческая рациональность и/или поведение часто отклоняются от модели рациональности, используемой в теории игр. Теоретики игр отвечают, сравнивая свои предположения с предположениями, используемыми в физике . Таким образом, хотя их предположения не всегда верны, они могут рассматривать теорию игр как разумный научный идеал, аналогичный моделям, используемым физиками . Однако эмпирическая работа показала, что в некоторых классических играх, таких как игра «Сороконожка» ( угадай 2/3 средней игры) и игра «Диктатор» , люди регулярно не играют в равновесия Нэша. Продолжаются споры о важности этих экспериментов и о том, полностью ли анализ экспериментов отражает все аспекты соответствующей ситуации. ^[б]

Некоторые теоретики игр, следуя работам Джона Мейнарда Смита и Джорджа Р. Прайса , обратились к эволюционной теории игр, чтобы решить эти проблемы. Эти модели предполагают либо отсутствие рациональности, либо ограниченную рациональность со стороны игроков. Несмотря на название, эволюционная теория игр не обязательно предполагает естественный отбор в биологическом смысле. Эволюционная теория игр включает как биологическую, так и культурную эволюцию, а также модели индивидуального обучения (например, динамику фиктивной игры ).

Предписывающий или нормативный анализ

	Сотрудничать	Дефект
Сотрудничать	-1, −1	-10, 0
Дефект	0, −10	-5, −5
Дилемма заключенного

Некоторые ученые рассматривают теорию игр не как инструмент прогнозирования поведения людей, а как предложение о том, как людям следует себя вести. Поскольку стратегия, соответствующая равновесию Нэша в игре, представляет собой лучший ответ на действия других игроков – при условии, что они находятся в (одном и том же) равновесии Нэша – игра по стратегии, которая является частью равновесия Нэша, кажется подходящей. Такое нормативное использование теории игр также подверглось критике. ^[75]

Использование теории игр в экономике

Теория игр — основной метод, используемый в математической экономике и бизнесе для моделирования конкурирующего поведения взаимодействующих агентов . ^[с]^[76]^[77]^[78] Приложения включают широкий спектр экономических явлений и подходов, таких как аукционы , переговоры , ценообразование при слияниях и поглощениях , ^[79] справедливое разделение , дуополии , олигополии , формирование социальных сетей , агентная вычислительная экономика , ^[80]^[81] общее равновесие , конструкция механизма, ^[82]^[83]^[84]^[85]^[86] и системы голосования ; ^[87] и в таких широких областях, как экспериментальная экономика, ^[88]^[89]^[90]^[91]^[92] поведенческая экономика , ^[93]^[94]^[95]^[96]^[97]^[98] информационная экономика , ^[45]^[46]^[47]^[48] промышленная организация , ^[99]^[100]^[101]^[102] и политическая экономия . ^[103]^[104]^[105]^[106]

Это исследование обычно фокусируется на определенных наборах стратегий, известных как «концепции решения» или «равновесия» . Распространено предположение, что игроки действуют рационально. В некооперативных играх самым известным из них является равновесие Нэша. Набор стратегий представляет собой равновесие Нэша, если каждая из них представляет собой лучший ответ на другие стратегии. Если все игроки применяют стратегии равновесия Нэша, у них нет одностороннего стимула отклоняться, поскольку их стратегия — лучшее, что они могут сделать, учитывая то, что делают другие. ^[107]^[108]

Выигрыши в игре обычно отражают полезность отдельных игроков.

Прототипическая статья по теории игр в экономике начинается с описания игры, которая представляет собой абстракцию конкретной экономической ситуации. Выбирается одна или несколько концепций решения, и автор демонстрирует, какие множества стратегий в представленной игре являются равновесиями соответствующего типа. Экономисты и профессора бизнеса предлагают два основных варианта использования (отмеченных выше): описательное и предписывающее . ^[70]

Применение в управленческой экономике

Теория игр также широко используется в определенной отрасли или направлении экономики – экономике управления . Одним из важных применений этого метода в области управленческой экономики является анализ стратегических взаимодействий между фирмами. ^[109] Например, фирмы могут конкурировать на рынке с ограниченными ресурсами, и теория игр может помочь менеджерам понять, как их решения влияют на конкурентов и на общие результаты рынка. Теорию игр также можно использовать для анализа сотрудничества между фирмами, например, при формировании стратегических альянсов или совместных предприятий. Еще одно применение теории игр в экономике управления — анализ стратегий ценообразования. Например, фирмы могут использовать теорию игр для определения оптимальной стратегии ценообразования на основе того, как, по их ожиданиям, конкуренты будут реагировать на их ценовые решения. В целом теория игр служит полезным инструментом для анализа стратегических взаимодействий и принятия решений в контексте экономики управления.

Использование теории игр в бизнесе

Сертифицированный институт закупок и поставок (CIPS) продвигает знания и использование теории игр в контексте деловых закупок . ^[110] Партнеры CIPS и TWS провели серию опросов, призванных изучить понимание, осведомленность и применение теории игр среди специалистов по закупкам . Некоторые из основных выводов третьего ежегодного опроса (2019 г.) включают:

применение теории игр в закупочной деятельности увеличилось – на тот момент оно составляло 19% среди всех респондентов опроса
65% участников прогнозируют, что использование приложений теории игр будет расти
70% респондентов говорят, что имеют «только базовое или не базовое понимание» теории игр.
20% участников прошли рабочем месте. обучение по теории игр на
50% респондентов заявили, что желательны новые или улучшенные программные решения.
90% респондентов заявили, что у них нет необходимого для работы программного обеспечения. ^[111]

Использование теории игр в управлении проектами

Разумное принятие решений имеет решающее значение для успеха проектов. В управлении проектами теория игр используется для моделирования процесса принятия решений участниками, такими как инвесторы, менеджеры проектов, подрядчики, субподрядчики, правительства и клиенты. Довольно часто эти игроки имеют конкурирующие интересы, а иногда их интересы наносят прямой ущерб другим игрокам, что делает сценарии управления проектами хорошо подходящими для моделирования с помощью теории игр.

Пиравенан (2019) ^[112] в своем обзоре приводит несколько примеров использования теории игр для моделирования сценариев управления проектами. Например, у инвестора обычно есть несколько вариантов инвестирования, и каждый вариант, скорее всего, приведет к созданию отдельного проекта, и, таким образом, один из вариантов инвестирования должен быть выбран до того, как будет составлен устав проекта. Аналогичным образом, любой крупный проект с участием субподрядчиков, например строительный проект, имеет сложное взаимодействие между главным подрядчиком (менеджером проекта) и субподрядчиками или между самими субподрядчиками, которое обычно имеет несколько точек принятия решений. Например, если в контракте между подрядчиком и субподрядчиком существует двусмысленность, каждый должен решить, насколько сильно продвигать свое дело, не ставя под угрозу весь проект и, следовательно, свою собственную долю в нем. Аналогичным образом, когда запускаются проекты конкурирующих организаций, сотрудники отдела маркетинга должны решить, какие сроки и стратегия лучше всего подходят для продвижения проекта или его результирующего продукта или услуги, чтобы он мог получить максимальную эффективность в условиях конкуренции. В каждом из этих сценариев необходимые решения зависят от решений других игроков, интересы которых каким-то образом конкурируют с интересами лица, принимающего решения, и поэтому в идеале их можно смоделировать с помощью теории игр.

Пиравенан ^[112] резюмирует, что игры для двух игроков преимущественно используются для моделирования сценариев управления проектами, и в зависимости от личности этих игроков в управлении проектами используются пять различных типов игр.

Игры между государством и частным сектором (игры, моделирующие государственно-частное партнерство )
Игры «Подрядчик-подрядчик»
Игры подрядчик-субподрядчик
Игры субподрядчик-субподрядчик
Игры с участием других игроков

Что касается типов игр, для моделирования различных сценариев управления проектами используются как кооперативные, так и некооперативные, нормальные и расширенные формы, игры с нулевой и ненулевой суммой.

Политология

Применение теории игр к политической науке сосредоточено на пересекающихся областях справедливого разделения , политической экономии , общественного выбора , военных переговоров , позитивной политической теории и теории социального выбора . В каждой из этих областей исследователи разработали теоретико-игровые модели, в которых игроками часто являются избиратели, государства, группы с особыми интересами и политики. ^[113]

Ранние примеры теории игр, примененные к политической науке, предоставлены Энтони Даунсом . В своей книге 1957 года «Экономическая теория демократии » ^[114] он применяет модель местоположения фирмы Хотеллинга к политическому процессу. В модели Даунсиана политические кандидаты придерживаются идеологий в одномерном политическом пространстве. Даунс сначала показывает, как политические кандидаты приблизятся к идеологии, предпочитаемой медианным избирателем, если избиратели будут полностью информированы, но затем утверждает, что избиратели предпочитают оставаться рационально невежественными, что допускает расхождения кандидатов. Теория игр была применена в 1962 году к кубинскому ракетному кризису во время президентства Джона Ф. Кеннеди. ^[115]

Было также высказано предположение, что теория игр объясняет стабильность любой формы политического правления. Возьмем, к примеру, простейший случай монархии: король, будучи всего лишь одним человеком, не поддерживает и не может поддерживать свою власть, лично осуществляя физический контроль над всеми или даже каким-либо значительным числом своих подданных. Вместо этого суверенный контроль объясняется признанием каждым гражданином того, что все остальные граждане ожидают, что друг от друга будут рассматривать короля (или другое установленное правительство) как человека, чьи приказы будут выполняться. Координация общения между гражданами с целью замены суверена фактически запрещена, поскольку заговор с целью замены суверена обычно наказуем как преступление. ^[116] Таким образом, в процессе, который можно смоделировать вариантами дилеммы узника, в периоды стабильности ни один гражданин не сочтет целесообразным заменить суверена, даже если все граждане знают, что для них было бы лучше, если бы они все начали действовать. коллективно. ^{[ нужна ссылка ]}

Теоретико-игровое объяснение демократического мира заключается в том, что публичные и открытые дебаты в демократических странах посылают четкую и надежную информацию об их намерениях другим государствам. Напротив, трудно понять намерения недемократических лидеров, какой эффект окажут уступки и будут ли выполняться обещания. Таким образом, возникнет недоверие и нежелание идти на уступки, если хотя бы одна из сторон в споре — недемократия. ^[117]

Однако теория игр предсказывает, что две страны все равно могут начать войну, даже если их лидеры осознают цену боевых действий. Война может возникнуть из-за асимметричной информации; У двух стран могут быть стимулы искажать объем имеющихся у них военных ресурсов, что делает их неспособными урегулировать споры мирным путем, не прибегая к боевым действиям. Более того, война может возникнуть из-за проблем с обязательствами: если две страны желают урегулировать спор мирными средствами, но каждая хочет вернуться к условиям этого урегулирования, у них может не быть другого выбора, кроме как прибегнуть к войне. Наконец, война может возникнуть из-за неделимости проблем. ^[118]

Теория игр также может помочь предсказать реакцию нации, когда к этой нации будут применяться новые правила или законы. Одним из примеров является исследование Питера Джона Вуда (2013), посвященное тому, что страны могут сделать, чтобы помочь уменьшить изменение климата. Вуд считал, что этого можно достичь, заключив договоры с другими странами о сокращении выбросов парниковых газов . Однако он пришел к выводу, что эта идея не сработает, поскольку создаст для народов дилемму заключенного. ^[119]

Использование теории игр в оборонной науке и технологиях

Теория игр широко использовалась для моделирования сценариев принятия решений, имеющих отношение к оборонным приложениям. ^[120] Большинство исследований, в которых теория игр применялась в оборонных условиях, связаны с войной командования и контроля и могут быть далее классифицированы на исследования, посвященные (i) войне за распределение ресурсов (ii) информационной войне (iii) войне за контроль над оружием и (iv) противнику. Мониторинг войны. ^[120] Многие из изученных проблем связаны с обнаружением и отслеживанием, например, надводный корабль пытается отследить вражескую подводную лодку, а подводная лодка пытается уклониться от слежения, а также с взаимозависимым принятием решений, которые происходят в отношении пеленга, скорости и датчика. технология активирована обоими судами. Хо и др. ^[120] представляет собой краткое изложение современного состояния использования теории игр в оборонных приложениях и подчеркивает преимущества и ограничения теории игр в рассматриваемых сценариях.

Использование теории игр в биологии

	Ястреб	Где
Ястреб	20, 20	80, 40
Где	40, 80	60, 60
« ястреб -голубь» Игра

В отличие от экономических, выигрыши в играх в биологии часто интерпретируются как соответствующие приспособленности . Кроме того, основное внимание уделялось не столько равновесиям, которые соответствуют понятию рациональности, сколько тем, которые будут поддерживаться эволюционными силами. Самое известное равновесие в биологии известно как эволюционно стабильная стратегия (ESS), впервые представленная в ( Maynard Smith & Price 1973 ). Хотя ее первоначальная мотивация не включала в себя какие-либо ментальные требования равновесия Нэша, каждая ESS является равновесием Нэша.

В биологии теория игр использовалась как модель для понимания множества различных явлений. Впервые он был использован для объяснения эволюции (и стабильности) примерного соотношения полов 1:1 . ( Фишер 1930 ) предположил, что соотношение полов 1:1 является результатом эволюционных сил, действующих на людей, которые, как можно рассматривать, пытаются максимизировать количество своих внуков.

Кроме того, биологи использовали эволюционную теорию игр и ESS, чтобы объяснить возникновение общения животных . ^[121] Анализ сигнальных игр и других коммуникативных игр позволил понять эволюцию общения среди животных. Например, моббинговое поведение многих видов, при котором большое количество животных-жертв нападает на более крупного хищника, кажется примером спонтанной эмерджентной организации. Было также показано, что муравьи демонстрируют упреждающее поведение, похожее на моду (см. « Пола Ормерода » Экономика бабочек ).

Биологи использовали игру кур для анализа боевого поведения и территориальности. ^[122]

По словам Мейнарда Смита в предисловии к книге « Эволюция и теория игр» , «парадоксально, но оказалось, что теорию игр легче применить к биологии, чем к области экономического поведения, для которой она изначально была разработана». Эволюционная теория игр использовалась для объяснения многих, казалось бы, нелепых явлений в природе. ^[123]

Одно из таких явлений известно как биологический альтруизм . Это ситуация, в которой организм действует таким образом, который приносит пользу другим организмам и наносит вред самому себе. Это отличается от традиционных представлений об альтруизме, поскольку такие действия не являются сознательными, а кажутся эволюционными адаптациями, направленными на повышение общей приспособленности. Примеры можно найти у самых разных видов: от летучих мышей-вампиров, которые срыгивают кровь, полученную во время ночной охоты, и отдают ее членам группы, которые не смогли накормиться, до рабочих пчел, которые заботятся о пчелиной матке всю свою жизнь и никогда не спариваются. мартышки-верветки , которые предупреждают членов группы о приближении хищника, даже если это ставит под угрозу шансы этого человека на выживание. ^[124] Все эти действия повышают общую подготовленность группы, но происходят за счет отдельного человека.

Эволюционная теория игр объясняет этот альтруизм идеей родственного отбора . Альтруисты различают людей, которым они помогают, и отдают предпочтение родственникам. Правило Гамильтона объясняет эволюционное обоснование этого выбора с помощью уравнения $c < b \times r$ , где стоимость c для альтруиста должно быть меньше, чем выгода б получателю, умноженному на коэффициент родства р . Более близкородственные два организма вызывают увеличение случаев альтруизма, поскольку они имеют много одинаковых аллелей. Это означает, что альтруистический индивидуум, гарантируя, что аллели его близкого родственника передаются через выживание его потомства, может отказаться от возможности иметь потомство, поскольку передается такое же количество аллелей. Например, помощь брату или сестре (у диплоидных животных) имеет коэффициент 1 ⁄ 2 , потому что (в среднем) особь разделяет половину аллелей с потомством своего брата или сестры. Обеспечение того, чтобы достаточное количество потомков брата или сестры дожило до взрослого возраста, исключает необходимость производства потомства у альтруистической личности. ^[124] Значения коэффициентов сильно зависят от объема игрового поля; например, если выбор, кому отдать предпочтение, включает в себя все генетические живые существа, а не только всех родственников, мы предполагаем, что несоответствие между всеми людьми составляет только примерно 1% разнообразия в игровом поле, коэффициент, который был 1 ⁄ 2 в меньшем поле становится 0,995. Аналогичным образом, если принять во внимание, что информация, отличная от генетической природы (например, эпигенетика, религия, наука и т. д.), сохранялась во времени, игровое поле становится еще больше, а расхождения уменьшаются.

Информатика и логика

Теория игр стала играть все более важную роль в логике и информатике . Несколько логических теорий имеют основу в семантике игр . Кроме того, ученые-компьютерщики использовали игры для моделирования интерактивных вычислений . Кроме того, теория игр обеспечивает теоретическую основу для многоагентных систем . ^[125]

Отдельно теория игр сыграла роль в онлайн-алгоритмах ; в частности, проблема k -сервера , которую в прошлом называли играми с движущимися издержками и играми запрос-ответ . ^[126] Принцип Яо — это теоретико-игровой метод доказательства нижних границ вычислительной сложности , рандомизированных алгоритмов особенно онлайн-алгоритмов.

Появление Интернета стимулировало разработку алгоритмов поиска равновесия в играх, рынках, вычислительных аукционах, одноранговых системах, а также на рынках безопасности и информации. Алгоритмическая теория игр ^[86] и внутри него проектирование алгоритмических механизмов ^[85] объединить разработку вычислительных алгоритмов и анализ сложных систем с экономической теорией. ^[127]^[128]^[129]

Философия

	Олень	заяц
Олень	3, 3	0, 2
заяц	2, 0	2, 2
Охота на оленя

Теория игр нашла несколько применений в философии . Отвечая на две статьи У.В.О. Куайна ( 1960 , 1967 ), Льюис (1969) использовал теорию игр для разработки философского объяснения конвенции . При этом он провел первый анализ общеизвестных знаний и применил их при анализе координационных игр . можно Кроме того, он впервые предположил, что понимать смысл с точки зрения сигнальных игр . Это более позднее предложение развивалось несколькими философами после Льюиса. ^[130]^[131] Следуя Льюиса (1969) теоретико-игровому описанию конвенций , Эдна Ульманн-Маргалит (1977) и Биккьери (2006) разработали теории социальных норм , которые определяют их как равновесия Нэша, возникающие в результате преобразования игры со смешанными мотивами в координационную игру. ^[132]^[133]

Теория игр также заставила философов мыслить в терминах интерактивной эпистемологии : что значит для коллектива иметь общие убеждения или знания и каковы последствия этого знания для социальных результатов, возникающих в результате взаимодействия агентов. Среди философов, работавших в этой области, — Биккьери (1989, 1993), ^[134]^[135] Скирмс (1990), ^[136] и Сталнакер (1999). ^[137]

Синтез теории игр с этикой отстаивал Р.Б. Брейтуэйт . ^[138] Была надежда, что строгий математический анализ теории игр поможет формализовать более неточные философские дискуссии. Однако эти ожидания оправдались лишь в ограниченной степени. ^[139]

В этике некоторые (особенно Дэвид Готье, Грегори Кавка и Джин Хэмптон) ^{[ ВОЗ? ]} авторы пытались реализовать проект Томаса Гоббса о выводе морали из личных интересов. Поскольку такие игры, как «Дилемма заключенного», представляют собой очевидный конфликт между моралью и личными интересами, важным компонентом этого проекта является объяснение того, почему сотрудничество необходимо ради собственных интересов. Эта общая стратегия является компонентом общего взгляда на общественный договор в политической философии (см., например, Готье (1986) и Кавку (1986) ). ^[д]

Другие авторы пытались использовать эволюционную теорию игр, чтобы объяснить возникновение человеческих взглядов на мораль и соответствующее поведение животных. Эти авторы рассматривают несколько игр, включая дилемму заключённого, охоту на оленя и торговую игру Нэша , как объясняющие возникновение взглядов на мораль (см., например, Skyrms ( 1996 , 2004 ) и Sober and Wilson ( 1998 )).

Эпидемиология

Поскольку решение о вакцинации против конкретного заболевания часто принимается отдельными людьми, которые при принятии этого решения могут учитывать ряд факторов и параметров (таких как заболеваемость и распространенность заболевания, предполагаемые и реальные риски, связанные с заражением этим заболеванием). (уровень смертности, предполагаемые и реальные риски, связанные с вакцинацией, а также финансовые затраты на вакцинацию), теория игр использовалась для моделирования и прогнозирования распространения вакцинации в обществе. ^[140]^[141]

Искусственный интеллект и машинное обучение

Теория игр имеет множество приложений в области искусственного интеллекта и машинного обучения. Его часто используют при разработке автономных систем, способных принимать сложные решения в неопределенной среде. ^[142] Некоторые другие области применения теории игр в контексте AI/ML заключаются в следующем: формирование многоагентных систем, обучение с подкреплением, ^[143] конструкция механизма и т. д. ^[144] Используя теорию игр для моделирования поведения других агентов и прогнозирования их действий, системы искусственного интеллекта и машинного обучения могут принимать более правильные решения и работать более эффективно. ^[145]

Известные примеры игр

Дилемма заключенного

Стандартная матрица выигрышей для дилеммы заключенного
Б А	Б остается тихий	Б предает
А остается тихий	−2 −2	0 −10
А предает	−10 0	−5 −5

Уильям Паундстоун описал эту игру в своей книге «Дилемма узника» 1993 года: ^[146]

Двое членов преступной группировки, А и Б, арестованы и заключены в тюрьму. Каждый заключенный находится в одиночной камере без возможности общения со своим партнером. Основное обвинение влечет за собой наказание в виде десяти лет тюремного заключения; однако у полиции нет доказательств для вынесения обвинительного приговора. Они планируют приговорить обоих к двум годам тюремного заключения по менее серьезному обвинению, но предлагают каждому заключенному фаустовскую сделку: если один из них сознается в преступлении по основному обвинению, предавая другого, они будут помилованы и смогут уйти, в то время как другой должен отбыть весь срок наказания вместо двух лет по менее строгому обвинению.

Доминирующая стратегия (и, следовательно, лучший ответ на любую возможную стратегию противника) — предать другого, что соответствует принципу уверенности . ^[147] Однако молчание обоих заключенных принесет им обоим большую награду, чем взаимное предательство.

Битва полов

«Битва полов» — это термин, используемый для описания предполагаемого конфликта между мужчинами и женщинами в различных сферах жизни, таких как отношения, карьера и социальные роли. Этот конфликт часто изображается в популярной культуре, например, в фильмах и телешоу, как юмористическое или драматическое соревнование между полами. Этот конфликт можно описать в рамках теории игр. Это пример некооперативных игр.

Пример «битвы полов» можно увидеть в изображении отношений в популярных средствах массовой информации, где мужчины и женщины часто изображаются принципиально разными и конфликтующими друг с другом. Например, в некоторых романтических комедиях главные герои мужского и женского пола имеют противоположные взгляды на любовь и отношения, и им приходится преодолевать эти различия, чтобы быть вместе. ^[148]

В этой игре существуют два равновесия Нэша в чистой стратегии: одно, когда оба игрока выбирают одну и ту же стратегию, и другое, когда игроки выбирают разные варианты. Если игра ведется в смешанных стратегиях, где каждый игрок выбирает свою стратегию случайным образом, то существует бесконечное число равновесий Нэша. Однако в контексте игры «битва полов» обычно делается предположение, что игра ведется в чистых стратегиях. ^[149]

Ультиматум игра

Игра «Ультиматум» — игра, ставшая популярным инструментом экономических экспериментов . Раннее описание принадлежит нобелевскому лауреату Джону Харсаньи в 1961 году. ^[150]

Один игрок, предлагающий, получает определенную сумму денег. Предлагающему поручено разделить его с другим игроком, отвечающим (который знает, какова общая сумма). Как только предлагающий сообщает о своем решении, ответчик может принять его или отклонить. Если ответчик соглашается, деньги делятся в зависимости от предложения; если ответчик отклоняет предложение, оба игрока ничего не получают. Оба игрока заранее знают последствия принятия или отклонения предложения ответчиком. Игра демонстрирует, как общественное признание, справедливость и щедрость влияют на решения игроков. ^[151]

У игры «Ультиматум» есть вариант — игра «Диктатор». Они в основном идентичны, за исключением того, что в игре с диктатором ответчик не имеет права отклонить предложение предлагающего.

Доверительная игра

«Игра в доверие» — это эксперимент, призванный измерить доверие к экономическим решениям. Ее еще называют «инвестиционной игрой», и она предназначена для исследования доверия и демонстрации его важности, а не «рациональности» личных интересов. Игра была разработана Бергом Джойсом, Джоном Дикхо и Кевином Маккейбом в 1995 году. ^[152]

В игре одному игроку (инвестору) дается определенная сумма денег, и он должен решить, какую часть ее передать другому игроку (доверительному управляющему). Затем экспериментатор утраивает данное количество. Затем доверительный управляющий решает, какую часть утроенной суммы вернуть инвестору. Если получатель полностью заинтересован в себе, то он/она не должен ничего возвращать. Однако это не так, как проводится эксперимент. Результаты показывают, что люди готовы оказать доверие, рискуя некоторой суммой денег, полагая, что будет взаимность. ^[153]

Конкурс Курно

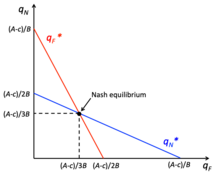
Модель конкуренции Курно предполагает, что игроки выбирают количество однородного продукта для производства независимо и одновременно, при этом предельные издержки могут быть разными для каждой фирмы, а выигрышем фирмы является прибыль. Издержки производства являются общедоступной информацией, и фирма стремится определить объем, максимизирующий прибыль, исходя из того, что, по ее мнению, будет производить другая фирма и вести себя как монополия. В этой игре фирмы хотят производить монопольный объем, но у них есть сильный стимул отклоняться и производить больше, что снижает рыночную цену. ^[23] Например, у фирм может возникнуть соблазн отклониться от монопольного количества, если существует низкое монопольное количество и высокая цена, с целью увеличения производства для максимизации прибыли. ^[23] Однако этот вариант не обеспечивает наибольшую отдачу, поскольку способность фирмы максимизировать прибыль зависит от ее доли на рынке и эластичности рыночного спроса. ^[154] Равновесие Курно достигается, когда каждая фирма действует в соответствии со своей функцией реакции, не имея стимула к отклонению, поскольку у них есть лучший ответ, основанный на выпуске другой фирмы. ^[23] В игре фирмы достигают равновесия Нэша, когда достигается равновесие Курно.

Бертран Конкурс

Конкуренция Бертрана предполагает однородность продуктов и постоянные предельные издержки, а цены выбирают игроки. ^[23] Равновесие ценовой конкуренции – это ситуация, когда цена равна предельным издержкам при условии полной информации о издержках конкурентов. Следовательно, у фирм есть стимул отклоняться от равновесия, поскольку однородный продукт с более низкой ценой получит всю долю рынка, что известно как преимущество в издержках. ^[155]

В популярной культуре

По мотивам книги Сильвии Назар 1998 года . ^[156] История жизни теоретика игр и математика Джона Нэша была превращена в биографический фильм 2001 года «Игры разума » с Расселом Кроу в роли Нэша. ^[157]
» 1959 года В военно-фантастическом романе Звездный десант « Роберта А. Хайнлайна упоминаются «теория игр» и «теория игр». ^[158] фильме 1997 года В одноименном персонаж Карл Дженкинс назвал свое задание в военной разведке «играми и теорией».
Фильм 1964 года « Доктор Стрейнджлав» высмеивает идеи теории игр о теории сдерживания . Например, ядерное сдерживание зависит от угрозы катастрофического возмездия в случае обнаружения ядерного нападения. Теоретик игр может утверждать, что такие угрозы могут оказаться неправдоподобными в том смысле, что они могут привести к несовершенному равновесию на подыграх. Фильм развивает эту идею еще на один шаг вперед: Советский Союз безвозвратно берет на себя обязательство нанести катастрофический ядерный ответ, не обнародовав угрозу. ^[159]
1980-х годов Пауэр-поп- группа Game Theory была основана певцом и автором песен Скоттом Миллером , который описал название группы как намек на «исследование расчета наиболее подходящих действий с учетом противника … чтобы свести к минимуму количество неудач». ^[160]
«Игра лжеца» , японская манга 2005 года и телесериал 2007 года, представляет главным героям каждого эпизода игру или задачу, которая обычно берется из теории игр, что демонстрируется стратегиями, применяемыми персонажами. ^[161]
В романе Шпионская история» « Лена Дейтона 1974 года исследуются элементы теории игр применительно к учениям армии времен холодной войны.
Роман Темный лес» « Лю Цысиня 2008 года исследует взаимосвязь между внеземной жизнью, человечеством и теорией игр.
Джокер, главный антагонист фильма 2008 года «Темный рыцарь» , представляет концепции теории игр, в частности дилемму заключенного в сцене, где он просит пассажиров двух разных паромов взорвать другой, чтобы спасти своих.
В фильме 2018 года « Безумно богатые азиаты» главная женская роль Рэйчел Чу — профессор экономики и теории игр в Нью-Йоркском университете . В начале фильма она показана в своем классе Нью-Йоркского университета, играющей в покер со своим ассистентом преподавателя, и выигрывает игру, блефуя ; ^[162] затем, в кульминации фильма, она играет в маджонг с неодобрительной матерью своего парня Элеонорой, намеренно проигрывая игру Элеоноре, но в результате завоевав ее одобрение. ^[163]
В фильме 2017 года «Игра Молли » Брэд, неопытный игрок в покер, принимает иррациональное решение о ставке, не осознавая этого, и заставляет своего противника Харлана отклониться от его стратегии равновесия Нэша, что приводит к значительному проигрышу, когда Харлан теряет руку. ^[164]

См. также

Прикладная этика - Практическое применение моральных соображений
Игра с разделением полосы пропускания - тип игры с распределением ресурсов.
Парадокс сетевого магазина - Парадокс теории игр
Коллективная интенциональность - интенциональность, возникающая, когда два или более человека вместе выполняют задачу.
Ядро (теория игр) - термин в теории игр.
Глоссарий теории игр - Список определений терминов и понятий, используемых в теории игр.
Переговоры внутри домохозяйства – переговоры между членами домохозяйства для принятия решений.
Сценарий Kingmaker - эндшпильная ситуация, когда игрок, который не может выиграть, имеет возможность определить, какой игрок среди других выиграет.
Право и экономика – Применение экономической теории к анализу правовых систем
Гарантированное взаимное уничтожение – Доктрина военной стратегии
Краткое описание искусственного интеллекта - Обзор и актуальное руководство по искусственному интеллекту.
Парадокс Паррондо - Парадокс в теории игр
Принцип предосторожности – Стратегия управления рисками
Квантовая судейская игра
Управление рисками – идентификация, оценка и контроль рисков.
Самоподтверждающееся равновесие
Трагедия общего достояния : личные интересы приводят к истощению общего ресурса.
Дилемма путешественника – мысленный эксперимент в игре с ненулевой суммой.
Доктрина Вильсона (экономика) - Аргумент в экономической теории
Композиционная теория игр

Списки

Примечания

↑ Хотя общеизвестные знания были впервые обсуждены философом Дэвидом Льюисом в его диссертации (а затем и книге) «Конвенция» в конце 1960-х годов, экономисты не рассматривали их широко до Роберта Ауманна в 1970-х годах. работы
^ Экспериментальная работа в теории игр имеет много названий: экспериментальная экономика , поведенческая экономика и поведенческая теория игр . ^[74]
^ В JEL: C7 классификационных кодов Журнала экономической литературы .
^ Более подробное обсуждение использования теории игр в этике см. в Стэнфордской энциклопедии философии вступительной теории игр и этики .

Ссылки

^ Перейти обратно: ^а ^б Майерсон, Роджер Б. (1991). Теория игр: анализ конфликта . Издательство Гарвардского университета . ISBN 9780674341166 .
^ Шепли, Ллойд С.; Шубик, Мартин (1 января 1971 г.). «Глава 1, Введение, Использование моделей». Теория игр в экономике . Архивировано из оригинала 23 апреля 2023 года . Проверено 23 апреля 2023 г.
^ Нойманн, Джон фон; Моргенштерн, Оскар (8 апреля 2007 г.). Теория игр и экономического поведения . Издательство Принстонского университета. ISBN 978-0-691-13061-3 . Архивировано из оригинала 28 марта 2023 года . Проверено 23 апреля 2023 г.
^ Нисан (2020). «Отчет о книге: Теория игр и экономического поведения (фон Нейман и Моргенштерн)» . lesswrong.com .
^ Хан, Фейсал Шах; Солмейер, Нил; Балу, Радхакришнан; Скромный, Трэвис С. (ноябрь 2018 г.). «Квантовые игры: обзор истории, современное состояние и интерпретация». Квантовая обработка информации . 17 (11): 309. Бибкод : 2018QuIP...17..309К . дои : 10.1007/s11128-018-2082-8 .
^ Мартин, Брайан (1978). «Избирательная полезность теории игр». Социальные исследования науки . 8 (1): 85–110. дои : 10.1177/030631277800800103 . JSTOR 284857 . Тем не менее, математические методы, используемые в теории игр, направлены на достижение единственной цели: максимизация «уровня безопасности», где уровень безопасности — это наименьшая сумма, которую игрок может получить от выбора стратегии.
^ Шафер, Г. (2018, декабрь). Теоретико-игровые основы вероятности Паскаля и Гюйгенса . Лекция Сартона, Школа архитектуры и инженерии, Гентский университет. [1]
^ Беллхаус, Дэвид Р. (2007), «Проблема Уолдегрейва» (PDF) , Journal Électronique d'Histoire des Probabilités et de la Statistique [ Электронный журнал истории вероятностей и статистики ], 3 (2), в архиве (PDF) с сайта оригинал от 20 августа 2008 г.
^ Беллхаус, Дэвид Р. (2015). «Ле Хер и другие проблемы вероятности, обсуждаемые Бернулли, Монмором и Уолдегрейвом». Статистическая наука . 30 (1). Институт математической статистики : 26–39. arXiv : 1504.01950 . Бибкод : 2015arXiv150401950B . дои : 10.1214/14-STS469 . S2CID 59066805 .
^ Цермело, Эрнст (1913). Хобсон, EW; Любовь, AEH (ред.). Über eine Anwendung der Mengenlehre auf die Theorie des Schachspiels [ О применении теории множеств к теории игры в шахматы ] (PDF) . Труды Пятого Международного конгресса математиков (1912 г.) (на немецком языке). Кембридж: Издательство Кембриджского университета. стр. 501–504. Архивировано из оригинала (PDF) 31 июля 2020 года . Проверено 29 августа 2019 г.
^ Ким, Сунгук, изд. (2014). Применение теории игр в сетевом проектировании . IGI Global. п. 3. ISBN 978-1-4666-6051-9 .
^ фон Нейман, Джон (1928). «К теории игр стратегии». Математические Анналы [ Mathematical Annals ] (на немецком языке). 100 (1): 295–320. дои : 10.1007/BF01448847 . S2CID 122961988 .
^ фон Нейман, Джон (1959). «К теории игр-стратегий» . В Такере, штат Аризона; Люси, Р.Д. (ред.). Вклад в теорию игр . Том. 4. Перевод Баргманна, Сони. Принстон, Нью-Джерси : Издательство Принстонского университета . стр. 13–42. ISBN 0-691-07937-4 .
^ Мировский, Филип (1992). «Чего пытались достичь фон Нейман и Моргенштерн?» . В Вайнтраубе, Э. Рой (ред.). К истории теории игр . Дарем: Издательство Университета Дьюка. стр. 113–147. ISBN 978-0-8223-1253-6 .
^ Леонард, Роберт (2010), Фон Нейман, Моргенштерн и создание теории игр , Нью-Йорк: Издательство Кембриджского университета, номер документа : 10.1017/CBO9780511778278 , ISBN 978-0-521-56266-9
^ Кун, Стивен (4 сентября 1997 г.). Залта, Эдвард Н. (ред.). «Дилемма заключенного» . Стэнфордская энциклопедия философии . Стэнфордский университет. Архивировано из оригинала 18 января 2012 года . Проверено 3 января 2013 г.
^ Шор, Майк. «Некооперативная игра» . GameTheory.net . Архивировано из оригинала 1 апреля 2014 года . Проверено 15 сентября 2016 г.
^ Чандрасекаран, Рамасвами. «Теория кооперативных игр» (PDF) . Техасский университет в Далласе. Архивировано (PDF) из оригинала 18 апреля 2016 г.
^ Бранденбургер, Адам. «Теория кооперативных игр: характеристические функции, распределение, предельный вклад» (PDF) . Архивировано из оригинала (PDF) 29 августа 2017 года . Проверено 14 апреля 2020 г.
^ Шор, Майк (2006). «Симметричная игра» . Теория игр.net .
^ Оуэн, Гильермо (1995). Теория игр: Третье издание . Бингли: Издательство Emerald Group. п. 11. ISBN 978-0-12-531151-9 .
^ Чанг, Куан-Хуа (2015). «Решения в инженерном проектировании». Теория проектирования и методы с использованием CAD/CAE . стр. 39–101. дои : 10.1016/b978-0-12-398512-5.00002-5 . ISBN 978-0-12-398512-5 .
^ Перейти обратно: ^а ^б ^с ^д ^и Гиббонс, Роберт (1992). Теория игр для экономистов-прикладников . Принстон, Нью-Джерси: Издательство Принстонского университета. стр. 14–17. ISBN 0-691-04308-6 .
^ Фергюсон, Томас С. «Теория игр» (PDF) . Математический факультет Калифорнийского университета в Лос-Анджелесе. стр. 56–57. Архивировано (PDF) из оригинала 30 июля 2004 г.
^ Мысельский, Ян (1992). «Игры с совершенной информацией». Справочник по теории игр с экономическими приложениями . Том. 1. С. 41–70. дои : 10.1016/S1574-0005(05)80006-2 . ISBN 978-0-4448-8098-7 .
^ «Бесконечные шахматы» . Бесконечный сериал PBS . 2 марта 2017 г. Архивировано из оригинала 28 октября 2021 г. Совершенная информация определена в 0:25, с академическими источниками arXiv : 1302.4377 и arXiv : 1510.08155 .
^ Оуэн, Гильермо (1995). Теория игр: Третье издание . Бингли: Издательство Emerald Group. п. 4. ISBN 978-0-12-531151-9 .
^ Мирман, Леонард Дж. (1989). «Идеальная информация». Теория игр . стр. 194–198. дои : 10.1007/978-1-349-20181-5_22 . ISBN 978-0-333-49537-7 .
^ Мирман, Леонард (1989). Совершенная информация . Лондон: Пэлгрейв Макмиллан. стр. 194–195. ISBN 978-1-349-20181-5 .
^ Шохам и Лейтон-Браун (2008) , с. 60.
^ Осборн, Мартин Дж. (2000). Введение в теорию игр . Издательство Оксфордского университета. стр. 271–272.
^ Осборн, Мартин Дж (2020). Введение в теорию игр . Издательство Оксфордского университета. стр. 271–277.
^ Перейти обратно: ^а ^б Йорг Беверсдорф (2005). «31». Удача, логика и белая ложь: математика игр . AK Peters, Ltd., стр. ix–xii. ISBN 978-1-56881-210-6 .
^ Альберт, Майкл Х .; Новаковски, Ричард Дж.; Вулф, Дэвид (2007), Уроки игры: введение в комбинаторную теорию игр , AK Peters Ltd, стр. 3–4, ISBN 978-1-56881-277-9
^ Бек, Йожеф (2008). Комбинаторные игры: теория крестиков-ноликов . Издательство Кембриджского университета. стр. 1–3 . ISBN 978-0-521-46100-9 .
^ Хирн, Роберт А.; Демейн, Эрик Д. (2009), Игры, головоломки и вычисления , AK Peters, Ltd., ISBN 978-1-56881-322-6
^ Джонс, М. Тим (2008). Искусственный интеллект: системный подход . Джонс и Бартлетт Обучение. стр. 106–118. ISBN 978-0-7637-7337-3 .
^ Петросян, Луизиана; Мурзов, Н. В. (1966). «Теоретико-игровые задачи механики». Литовск. Мат. Сб. (на русском языке). 6 : 423–433.
^ Ньютон, Джонатан (2018). «Эволюционная теория игр: Возрождение» . Игры . 9 (2): 31. дои : 10.3390/g9020031 . hdl : 10419/179191 .
^ Уэбб (2007) .
^ Лозовану, Д; Пикл, С (2015). Теоретико-игровой подход к марковским процессам принятия решений, стохастическим позиционным играм и моделям многокритериального управления . Спрингер, Чам. ISBN 978-3-319-11832-1 .
^ Осборн и Рубинштейн (1994) .
^ Перейти обратно: ^а ^б МакМахан, Хью Брендан (2006). Надежное планирование в областях со стохастическими результатами, противниками и частичной наблюдаемостью (PDF) (кандидатская диссертация). Университет Карнеги-Меллон. стр. 3–4. Архивировано (PDF) из оригинала 1 апреля 2011 г.
^ Ховард (1971) .
^ Перейти обратно: ^а ^б Расмусен, Эрик (2007). Игры и информация (4-е изд.). Уайли. ISBN 978-1-4051-3666-2 .
^ Перейти обратно: ^а ^б Крепс, Дэвид М. (1990). Теория игр и экономическое моделирование . Издательство Оксфордского университета. дои : 10.1093/0198283814.001.0001 . ISBN 978-0-19-828381-2 . ^{[ нужна страница ]}
^ Перейти обратно: ^а ^б Ауманн, Р.Дж.; Харт, С., ред. (1992). Справочник по теории игр с экономическими приложениями . Эльзевир. ISBN 978-0-444-89427-4 . ^{[ нужна страница ]}
^ Перейти обратно: ^а ^б Ауманн, Роберт Дж.; Хейфец, Авиад (2002). «Глава 43 Неполная информация». Справочник по теории игр с экономическими приложениями, том 3 . Том. 3. стр. 1665–1686. дои : 10.1016/S1574-0005(02)03006-0 . ISBN 978-0-444-89428-1 .
^ Фуденберг, Дрю; Тироль, Жан (1991). Теория игр . С Прессой. п. 67. ИСБН 978-0-262-06141-4 .
^ Уильямс, Пол Д. (2013). Исследования безопасности: введение (второе изд.). Абингдон : Рутледж. стр. 55–56.
^ Шохам и Лейтон-Браун (2008) , с. 35.
^ $2^{N}$ обозначает мощности набор $N$ .
^ Тагиев, Рустам (3 мая 2011 г.). «Если для прогнозирования стратегического взаимодействия реальных агентов необходимо нечто большее, чем аналитическое моделирование». arXiv : 1105.0558 [ cs.GT ].
^ Розенталь, Роберт В. (декабрь 1973 г.). «Класс игр, обладающих чисто стратегическим равновесием Нэша». Международный журнал теории игр . 2 (1): 65–67. дои : 10.1007/BF01737559 . S2CID 121904640 .
^ Коллер, Дафна ; Мегиддо, Нимрод ; фон Стенгель, Бернхард (1994). «Быстрые алгоритмы поиска рандомизированных стратегий в деревьях игр». Материалы двадцать шестого ежегодного симпозиума ACM по теории вычислений – STOC '94 . стр. 750–759. дои : 10.1145/195058.195451 . ISBN 0-89791-663-8 . S2CID 1893272 .
^ Алур, Раджив; Дилл, Дэвид Л. (апрель 1994 г.). «Теория синхронизированных автоматов» . Теоретическая информатика . 126 (2): 183–235. дои : 10.1016/0304-3975(94)90010-8 .
^ Томлин, CJ; Лигерос, Дж.; Шанкар Шастри, С. (июль 2000 г.). «Теоретико-игровой подход к проектированию контроллеров для гибридных систем». Труды IEEE . 88 (7): 949–970. дои : 10.1109/5.871303 . S2CID 1844682 .
^ Коллер, Дафна; Пфеффер, Ави (июль 1997 г.). «Представления и решения теоретико-игровых задач». Искусственный интеллект . 94 (1–2): 167–215. дои : 10.1016/S0004-3702(97)00023-4 .
^ Майкл, Майкл Кернс; Литтман, Майкл Л. (2001). «Графические модели для теории игр». В УАИ : 253–260. CiteSeerX 10.1.1.22.5705 .
^ Кернс, Майкл; Литтман, Майкл Л.; Сингх, Сатиндер (7 марта 2011 г.). «Графические модели для теории игр». arXiv : 1301.2281 [ cs.GT ].
^ Лейтон Браун, Кевин; Тенненхольц, Моше (2005). Игры с локальными эффектами (PDF) . Материалы семинара Дагштуля. Центр компьютерных наук замка Дагштуль-Лейбница . Проверено 3 февраля 2023 г.
^ Генесерет, Михаил; С любовью, Натаниэль; Пелл, Барни (15 июня 2005 г.). «Общая игра: обзор соревнований AAAI». Журнал ИИ . 26 (2): 62. дои : 10.1609/aimag.v26i2.1813 .
^ Клемпнер, Хулио (2006). «Моделирование игр по кратчайшему пути с помощью сетей Петри: теория, основанная на Ляпунове» . Международный журнал прикладной математики и информатики . 16 (3): 387–397.
^ Санников, Юлий (сентябрь 2007 г.). «Игры с несовершенно наблюдаемыми действиями в непрерывном времени» (PDF) . Эконометрика . 75 (5): 1285–1329. дои : 10.1111/j.1468-0262.2007.00795.x .
^ Тагиев, Рустам (декабрь 2008 г.). «Мультиагентные игры Петри». 2008 Международная конференция по вычислительному интеллекту для моделирования управления и автоматизации . стр. 130–135. дои : 10.1109/CIMCA.2008.15 . ISBN 978-0-7695-3514-2 . S2CID 16679934 .
^ Тагиев, Рустам (2009). «О многоагентных моделях сетей Петри для вычисления обширных конечных игр». Новые вызовы в области вычислительного коллективного разума . Исследования в области вычислительного интеллекта. Том. 244. Спрингер. стр. 243–254. дои : 10.1007/978-3-642-03958-4_21 . ISBN 978-3-642-03957-7 .
^ Бхат, Навин; Лейтон-Браун, Кевин (11 июля 2012 г.). «Вычисление равновесия Нэша в играх с графом действий». arXiv : 1207.4128 [ cs.GT ].
^ Ларсон, Дженнифер М. (11 мая 2021 г.). «Сети конфликта и сотрудничества» . Ежегодный обзор политической науки . 24 (1): 89–107. doi : 10.1146/annurev-polisci-041719-102523 .
^ Фридман, Дэниел (1998). «Об экономических применениях эволюционной теории игр» (PDF) . Журнал эволюционной экономики . 8 : 14–53. Архивировано (PDF) из оригинала 11 февраля 2014 года.
^ Перейти обратно: ^а ^б Камерер, Колин Ф. (2003). «1.1 Для чего нужна теория игр?». Поведенческая теория игр: эксперименты по стратегическому взаимодействию . стр. 5–7. Архивировано из оригинала 14 мая 2011 года.
^ Браун, Будевейн де (сентябрь 2005 г.). «Теория игр в философии». Топои . 24 (2): 197–208. дои : 10.1007/s11245-005-5055-3 .
^ Росс, Дон (10 марта 2006 г.). «Теория игр» . В Залте, Эдвард Н. (ред.). Стэнфордская энциклопедия философии . Стэнфордский университет . Проверено 21 августа 2008 г.
^ Велегол, Даррелл; Сухи, Пол; Коннолли, Джон; Моррисси, Натали; Кук, Лаура (17 октября 2018 г.). «Химическая теория игр». Исследования в области промышленной и инженерной химии . 57 (41): 13593–13607. doi : 10.1021/acs.iecr.8b03835 . S2CID 105204747 .
^ Камерер, Колин Ф. (2003). "Введение". Поведенческая теория игр: эксперименты по стратегическому взаимодействию . стр. 1–25. Архивировано из оригинала 14 мая 2011 года.
^ Кадане, Джозеф Б.; Ларки, Патрик Д. (декабрь 1983 г.). «Путаница того, что есть и что должно быть в контексте теории игр». Наука управления . 29 (12): 1365–1379. дои : 10.1287/mnsc.29.12.1365 .
^ Ауманн, Роберт Дж. (2008). «теория игр» . Новый экономический словарь Пэлгрейва (2-е изд.). Архивировано из оригинала 15 мая 2011 года . Проверено 22 августа 2011 г.
^ Шубик, Мартин (1981). «Модели и методы теории игр в политической экономии». В «Стреле», Кеннет ; Интрилигатор, Майкл (ред.). Справочник по математической экономике, т. 1 . 1. Том. 1. С. 285–330. дои : 10.1016/S1573-4382(81)01011-4 . ISBN 978-0-444-86126-9 .
^ Шапиро, Карл (весна 1989 г.). «Теория бизнес-стратегии». Экономический журнал RAND . 20 (1). Уайли : 125–137. JSTOR 2555656 . ПМИД 10296625 . .
^ Агарвал, Н.; Зеефонгсекул, П. (11–12 декабря 2011 г.). Психологическое ценообразование в слияниях и поглощениях с использованием теории игр (PDF) . 19-й Международный конгресс по моделированию и симуляции . Перт . Проверено 3 февраля 2023 г.
^ Тесфацион, Ли (2006). Агентно-ориентированная вычислительная экономика: конструктивный подход к экономической теории . Справочник по вычислительной экономике. Том. 2. стр. 831–880. дои : 10.1016/S1574-0021(05)02016-2 . ISBN 978-0-444-51253-6 .
^ Джозеф Ю. Халперн (2008). «Информатика и теория игр» . Новый экономический словарь Пэлгрейва .
^ Майерсон, Роджер Б. (2008). «конструкция механизма» . Новый экономический словарь Пэлгрейва . Архивировано из оригинала 23 ноября 2011 года . Проверено 4 августа 2011 г.
^ Майерсон, Роджер Б. (2008). «принцип откровения» . Новый экономический словарь Пэлгрейва . Архивировано из оригинала 16 мая 2013 года . Проверено 4 августа 2011 г.
^ Сандхольм, Туомас (2008). «Компьютинг в проектировании механизмов» . Новый экономический словарь Пэлгрейва . Архивировано из оригинала 23 ноября 2011 года . Проверено 5 декабря 2011 г.
^ Перейти обратно: ^а ^б Нисан, Ноам; Ронен, Амир (апрель 2001 г.). «Проектирование алгоритмических механизмов». Игры и экономическое поведение . 35 (1–2): 166–196. дои : 10.1006/game.1999.0790 .
^ Перейти обратно: ^а ^б Нисан, Ноам ; Рафгарден, Тим; Тардос, Ева; Вазирани, Виджай В., ред. (2007). Алгоритмическая теория игр . Издательство Кембриджского университета . ISBN 9780521872829 . LCCN 2007014231 .
^ Брамс, Стивен Дж. (1994). Глава 30. Порядок голосования . Справочник по теории игр с экономическими приложениями. Том. 2. С. 1055–1089. дои : 10.1016/S1574-0005(05)80062-1 . ISBN 978-0-444-89427-4 . и Мулен, Эрве (1994). Глава 31 Социальный выбор . Справочник по теории игр с экономическими приложениями. Том. 2. С. 1091–1125. дои : 10.1016/S1574-0005(05)80063-3 . ISBN 978-0-444-89427-4 .
^ Смит, Вернон Л. (декабрь 1992 г.). «Теория игр и экспериментальная экономика: начало и ранние влияния». История политической экономии . 24 (Приложение): 241–282. doi : 10.1215/00182702-24-Supplement-241 .
^ Смит, Вернон Л. (2001). «Экспериментальная экономика». Международная энциклопедия социальных и поведенческих наук . стр. 5100–5108. дои : 10.1016/B0-08-043076-7/02232-4 . ISBN 978-0-08-043076-8 .
^ Плотт, Чарльз Р.; Смит, Вернон Л., ред. (2008). Справочник результатов экспериментальной экономики . Эльзевир. ISBN 978-0-08-088796-8 . ^{[ нужна страница ]}
^ Винсент П. Кроуфорд (1997). «Теория и эксперимент в анализе стратегического взаимодействия», в журнале «Достижения в области экономики и эконометрики: теория и приложения» , стр. 206–242. Архивировано 1 апреля 2012 г. в Wayback Machine . Кембридж. Перепечатано в книге Колина Ф. Камерера и др ., изд. (2003). Достижения поведенческой экономики , Принстон. Статьи 1986–2003 гг. Описание Архивировано 18 января 2012 года в Wayback Machine , предварительный просмотр , Принстон, гл. 12
^ Шубик, Мартин (2002). «Глава 62 Теория игр и экспериментальные игры». Справочник по теории игр с экономическими приложениями, том 3 . Том. 3. С. 2327–2351. дои : 10.1016/S1574-0005(02)03025-4 . ISBN 978-0-444-89428-1 .
^ Новый экономический словарь Пэлгрейва . 2008. Фарук Гюль . «Поведенческая экономика и теория игр». Абстрактный. Архивировано 7 августа 2017 года в Wayback Machine.
^ Камерер, Колин Ф. (2008). «Поведенческая теория игр» . Новый экономический словарь Пэлгрейва . Архивировано из оригинала 23 ноября 2011 года . Проверено 4 августа 2011 г.
^ Камерер, Колин Ф. (1997). «Прогресс в поведенческой теории игр» . Журнал экономических перспектив . 11 (4): 172. doi : 10.1257/jep.11.4.167 .
^ Камерер, Колин Ф. (2003). Поведенческая теория игр . Принстон. Описание. Архивировано 14 мая 2011 г. в Wayback Machine , предварительный просмотр. Архивировано 26 марта 2023 г. в Wayback Machine ([ctrl]+), и гл. 1 ссылка. Архивировано 4 июля 2013 г. на Wayback Machine .
^ Камерер, Колин Ф.; Левенштейн, Джордж; Рабин, Мэтью, ред. (2011). Достижения в поведенческой экономике . Издательство Принстонского университета. ISBN 978-1-4008-2911-8 . ^{[ нужна страница ]}
^ Фуденберг, Дрю (2006). «Продвижение за пределы достижений поведенческой экономики» . Журнал экономической литературы . 44 (3): 694–711. дои : 10.1257/jel.44.3.694 . JSTOR 30032349 . S2CID 3490729 .
^ Тироль, Жан (1988). Теория промышленной организации . МТИ Пресс. Описание и ссылки на предварительный просмотр глав, стр. vii–ix , «Общая организация», стр. 5–6 , и «Теория некооперативных игр: Руководство пользователя», гл. 11, стр. 423–59 .
^ Бэгвелл, Кайл; Волински, Ашер (2002). «Теория игр и промышленная организация». Справочник по теории игр с экономическими приложениями, том 3 . Том. 3. стр. 1851–1895. дои : 10.1016/S1574-0005(02)03012-6 . ISBN 978-0-444-89428-1 .
^ Фелс, Э.М. (1961). «Обзор стратегии и структуры рынка: конкуренция, олигополия и теория игр». Архив Weltwirtschaftliches . 87 : 12–14. JSTOR 40434883 .
^ Рид, Гэвин К. (1982). «Обзор структуры и поведения рынка». Экономический журнал . 92 (365): 200–202. дои : 10.2307/2232276 . JSTOR 2232276 .
^ Мартин Шубик (1981). «Модели и методы теории игр в политической экономии», в « Справочнике по математической экономике» , т. 1, стр. 285–330. два : 10.1016/S1573-4382(81)01011-4 .
^ Мартин Шубик (1987). Теоретико-игровой подход к политической экономии . МТИ Пресс. Описание . Архивировано 29 июня 2011 года в Wayback Machine.
^ Мартин Шубик (1978). «Теория игр: экономические приложения», в изд. В. Крускала и Дж. М. Танура, Международная энциклопедия статистики , т. 2, стр. 372–78.
^ Ауманн, Р.Дж.; Харт, С., ред. (1992). Справочник по теории игр с экономическими приложениями . Эльзевир. ISBN 978-0-444-89427-4 . ^{[ нужна страница ]}
^ Кристен, Маркус (1 июля 1998 г.). «Теоретико-игровая модель для изучения двух компромиссов при получении информации для тщательного балансирования» . ИНСЕАД . Архивировано из оригинала 24 мая 2013 года . Проверено 1 июля 2012 года .
^ Шевалье-Руаньян, Бенуа; Тригеоргис, Ленос (15 февраля 2012 г.). «Игры с опционами: баланс между гибкостью и обязательностью» . Европейский финансовый обзор . Архивировано из оригинала 20 июня 2013 года . Проверено 3 января 2013 г.
^ Уилкинсон, Ник (2005). «Теория игр». Управленческая экономика . стр. 331–381. дои : 10.1017/CBO9780511810534.015 . ISBN 978-0-521-81993-0 .
^ «Партнеры CIPS и TWS продвигают теорию игр на мировой арене» . 27 ноября 2020 г. Архивировано из оригинала 27 ноября 2020 г. . Проверено 20 апреля 2023 г.
^ CIPS (2021), Теория игр. Архивировано 11 апреля 2021 г. на Wayback Machine , CIPS совместно с TWS Partners, по состоянию на 11 апреля 2021 г.
^ Перейти обратно: ^а ^б Пиравинан, Махендра (2019). «Применение теории игр в управлении проектами: структурированный обзор и анализ» . Математика . 7 (9): 858. doi : 10.3390/math7090858 .
^ «Что теория игр говорит нам о политике и обществе» . Новости Массачусетского технологического института | Массачусетский технологический институт . 4 декабря 2018 г. Архивировано из оригинала 23 апреля 2023 г. Проверено 23 апреля 2023 г.
^ Даунс (1957) .
^ Брамс, Стивен Дж. (1 января 2001 г.). «Теория игр и Карибский кризис» . Плюс журнал . Архивировано из оригинала 24 апреля 2015 года . Проверено 31 января 2016 г.
^ «Как теория игр объясняет «иррациональное» поведение» . Массачусетский технологический институт Слоана . Архивировано из оригинала 23 апреля 2023 года . Проверено 23 апреля 2023 г.
^ Леви, Гилат; Разин, Ронни (март 2004 г.). «Требуются двое: объяснение демократического мира» . Журнал Европейской экономической ассоциации . 2 (1): 1–29. дои : 10.1162/154247604323015463 .
^ Фирон, Джеймс Д. (1 января 1995 г.). «Рационалистические объяснения войны». Международная организация . 49 (3): 379–414. дои : 10.1017/s0020818300033324 . JSTOR 2706903 . S2CID 38573183 .
^ Вуд, Питер Джон (февраль 2011 г.). «Изменение климата и теория игр» . Анналы Нью-Йоркской академии наук . 1219 (1): 153–170. Бибкод : 2011NYASA1219..153W . дои : 10.1111/j.1749-6632.2010.05891.x . ПМИД 21332497 .
^ Перейти обратно: ^а ^б ^с Хо, Эдвин; Раджагопалан, Арвинд; Скворцов, Алексей; Арулампалам, Санджив; Пиравинан, Махендра (28 января 2022 г.). «Теория игр в оборонных приложениях: обзор» . Датчики . 22 (3): 1032. arXiv : 2111.01876 . Бибкод : 2022Senso..22.1032H . дои : 10.3390/s22031032 . ПМЦ 8838118 . ПМИД 35161778 .
^ Харпер и Мейнард Смит (2003) .
^ Мейнард Смит, Джон (1974). «Теория игр и эволюция конфликтов животных» (PDF) . Журнал теоретической биологии . 47 (1): 209–221. Бибкод : 1974JThBi..47..209M . дои : 10.1016/0022-5193(74)90110-6 . ПМИД 4459582 .
^ Александр, Дж. Маккензи (19 июля 2009 г.). «Эволюционная теория игр» . В Залте, Эдвард Н. (ред.). Стэнфордская энциклопедия философии . Стэнфордский университет . Проверено 3 января 2013 г.
^ Перейти обратно: ^а ^б Окаша, Самир (3 июня 2003 г.). «Биологический альтруизм» . В Залте, Эдвард Н. (ред.). Стэнфордская энциклопедия философии . Стэнфордский университет . Проверено 3 января 2013 г.
^ Шохам, Йоав; Лейтон-Браун, Кевин (2008). Мультиагентные системы: алгоритмические, теоретико-игровые и логические основы . Издательство Кембриджского университета. ISBN 978-1-139-47524-2 . ^{[ нужна страница ]}
^ Бен-Дэвид и др. (1994) .
^ Халперн, Джозеф Ю. (2008). «Информатика и теория игр». Новый экономический словарь Пэлгрейва (2-е изд.).
^ Шохам, Йоав (август 2008 г.). «Информатика и теория игр». Коммуникации АКМ . 51 (8): 74–79. дои : 10.1145/1378704.1378721 .
^ Литтман, Эми; Литтман, Майкл Л. (2007). «Введение в специальный выпуск по обучению и вычислительной теории игр» . Машинное обучение . 67 (1–2): 3–6. дои : 10.1007/s10994-007-0770-1 . S2CID 22635389 .
^ Скирмс (1996)
^ Грим и др. (2004) .
^ Ульманн-Маргалит, Э. (1977), Появление норм , Oxford University Press, ISBN 978-0-19-824411-0 ^{[ нужна страница ]}
^ Биккьери, Кристина (2006), Грамматика общества: природа и динамика социальных норм , Cambridge University Press, ISBN 978-0-521-57372-6 ^{[ нужна страница ]}
^ Биккьери, Кристина (1989). «Самоопровергающие теории стратегического взаимодействия: парадокс общеизвестных». Эркеннтнис . 30 (1–2): 69–85. дои : 10.1007/BF00184816 . S2CID 120848181 .
^ Биккьери, Кристина (1993), Рациональность и координация , издательство Кембриджского университета , ISBN 978-0-521-57444-0
^ Скирмс, Брайан (1990), Динамика рационального обсуждения , издательство Гарвардского университета, ISBN 978-0-674-21885-7
^ Сталнакер, Роберт (октябрь 1996 г.). «Знания, убеждения и контрфактические рассуждения в играх». Экономика и философия . 12 (2): 133–163. дои : 10.1017/S0266267100004132 .
^ Брейтуэйт, Ричард Беван (1955). Теория игр как инструмент философа-моралиста. Вступительная лекция, прочитанная в Кембридже 2 декабря 1954 года . Университетское издательство. ISBN 978-0-521-11351-9 . ^{[ нужна страница ]}
^ Кун, Стивен Т. (июль 2004 г.). «Размышления об этике и теории игр». Синтезируйте . 141 (1): 1–44. дои : 10.1023/B:SYNT.0000035846.91195.cb .
^ Чанг, Шерил Л.; Пиравинан, Махендра; Паттисон, Филиппа; Прокопенко, Михаил (2020). «Теоретико-игровое моделирование динамики инфекционных заболеваний и методы вмешательства: обзор». Журнал биологической динамики . 14 (1): 57–89. arXiv : 1901.04143 . Бибкод : 2020JBioD..14...57C . дои : 10.1080/17513758.2020.1720322 . ПМИД 31996099 .
^ Робертс, Шивон (20 декабря 2020 г.). « Игра «Пандемия — это дилемма узника» » . Нью-Йорк Таймс .
^ Хэнли, Джон Т. (14 декабря 2021 г.). «ИГРЫ, теория игр и искусственный интеллект» . Журнал оборонной аналитики и логистики . 5 (2): 114–130. дои : 10.1108/JDAL-10-2021-0011 .
^ Альбрехт, Стефано В.; Кристианос, Филиппос; Шефер, Люк (2024). Многоагентное обучение с подкреплением: основы и современные подходы . С Прессой. ISBN 978-0-262-04937-5 . ^{[ нужна страница ]}
^ Парашар, Нилеш (15 августа 2022 г.). «Что такое теория игр в ИИ?» . Середина .
^ Хазра, Танмой; Анджария, Кушал (март 2022 г.). «Применение теории игр в глубоком обучении: обзор» . Мультимедийные инструменты и приложения . 81 (6): 8963–8994. дои : 10.1007/s11042-022-12153-2 . ПМК 9039031 . ПМИД 35496996 .
^ Паундстоун 1993 , стр. 8, 117.
^ Рапопорт, Анатолий (1987). «Дилемма заключенного». Новый экономический словарь Пэлгрейва . стр. 1–5. дои : 10.1057/978-1-349-95121-5_1850-1 . ISBN 978-1-349-95121-5 .
^ «Битва полов | История, участники и факты | Британника» . www.britanica.com . Архивировано из оригинала 23 апреля 2023 года . Проверено 23 апреля 2023 г.
^ Атенариум (12 августа 2020 г.). «Битва полов – равновесие Нэша в смешанных стратегиях координации» . Атенариум . Архивировано из оригинала 23 апреля 2023 года . Проверено 23 апреля 2023 г.
^ Харсаньи, Джон К. (июнь 1961 г.). «О постулатах рациональности, лежащих в основе теории кооперативных игр». Журнал разрешения конфликтов . 5 (2): 179–196. дои : 10.1177/002200276100500205 .
^ Аоки, Рюта; Ёмогида, Юкихито; Мацумото, Кендзи (январь 2015 г.). «Нейронные основы оценки социального равенства». Неврологические исследования . 90 : 33–40. дои : 10.1016/j.neures.2014.10.020 . ПМИД 25452125 .
^ Берг, Джойс; Дикхо, Джон; Маккейб, Кевин (июль 1995 г.). «Доверие, взаимность и социальная история». Игры и экономическое поведение . 10 (1): 122–142. дои : 10.1006/game.1995.1027 .
^ Джонсон, Ноэль Д.; Мислин, Александра А. (октябрь 2011 г.). «Игры на доверие: метаанализ». Журнал экономической психологии . 32 (5): 865–889. дои : 10.1016/j.joep.2011.05.007 .
^ «Равновесие Курно (Нэша)» . ОЭСР . 18 апреля 2013 г. Архивировано из оригинала 23 мая 2021 г. . Проверено 20 апреля 2021 г.
^ Спулбер, Дэниел Ф. (1995). «Конкуренция Бертрана, когда затраты соперников неизвестны». Журнал промышленной экономики . 43 (1): 1–11. дои : 10.2307/2950422 . JSTOR 2950422 .
^ Насар, Сильвия (1998) Прекрасный разум , Саймон и Шустер. ISBN 0-684-81906-6 .
^ Сингх, Саймон (14 июня 1998 г.). «Между гением и безумием» . Нью-Йорк Таймс .
^ Хайнлайн, Роберт А. (1959), Звездный десант
^ Доктор Стрейнджлав, или Как я научился не волноваться и полюбил бомбу . 29 января 1964 года. 51 минута. ... в том, что весь смысл машины судного дня утерян, если держать это в секрете!
^ Гузман, Рафер (6 марта 1996 г.). «Звезда в ожидании: верные поклонники, скудные продажи» . Тихоокеанское солнце . Архивировано из оригинала 6 ноября 2013 года . Проверено 25 июля 2018 г. .
^ «Игра лжеца (манга) - Anime News Network» . www.animenewsnetwork.com . Архивировано из оригинала 25 ноября 2022 года . Проверено 25 ноября 2022 г.
^ Чаффин, Шон (20 августа 2018 г.). «Покер и теория игр в популярном фильме «Безумно богатые азиаты» » . PokerNews.com. Архивировано из оригинала 5 ноября 2022 года . Проверено 5 ноября 2022 г.
^ Бин, Трэвис (8 февраля 2019 г.). «Теория игр в «Безумно богатых азиатах»: объяснение разборок в маджонге между Рэйчел и Элеонорой» . Колосс. Архивировано из оригинала 5 ноября 2022 года . Проверено 5 ноября 2022 г.
^ «Анализ применения сетей в «Игре Молли»: блог курса по сетям для INFO 2040/CS 2850/Econ 2040/SOC 2090» . Архивировано из оригинала 8 апреля 2023 года . Проверено 8 апреля 2023 г.

Источники

Бен-Дэвид, С.; Бородин А.; Карп, Р.; Тардос, Г.; Вигдерсон, А. (январь 1994 г.). «О силе рандомизации в онлайн-алгоритмах». Алгоритмика . 11 (1): 2–14. дои : 10.1007/BF01294260 . S2CID 26771869 .
Даунс, Энтони (1957), Экономическая теория демократии , Нью-Йорк: Харпер
Фишер, сэр Рональд Эйлмер (1930). Генетическая теория естественного отбора . Кларендон Пресс.
Готье, Дэвид (1986), Мораль по соглашению , Oxford University Press , ISBN 978-0-19-824992-4
Грим, Патрик; Кокалис, Трина; Алай-Тафти, Али; Килб, Николас; Сен-Дени, Поль (2004), «Делаем смысл возможным», Журнал экспериментального и теоретического искусственного интеллекта , 16 (4): 209–243, doi : 10.1080/09528130412331294715 , S2CID 5737352
Харпер, Дэвид ; Мейнард Смит, Джон (2003), Сигналы животных , Oxford University Press, ISBN 978-0-19-852685-8
Ховард, Найджел (1971), Парадоксы рациональности: игры, метаигры и политическое поведение , Кембридж, Массачусетс : The MIT Press, ISBN 978-0-262-58237-7
Кавка, Грегори С. (1986). Гоббсовская моральная и политическая теория . Издательство Принстонского университета. ISBN 978-0-691-02765-4 .
Льюис, Дэвид (1969), Конвенция: философское исследование , ISBN 978-0-631-23257-5 (издание 2002 г.)
Мейнард Смит, Джон ; Прайс, Джордж Р. (1973), «Логика конфликта животных», Nature , 246 (5427): 15–18, Бибкод : 1973Natur.246...15S , doi : 10.1038/246015a0 , S2CID 4224989
Осборн, Мартин Дж.; Рубинштейн, Ариэль (1994), Курс теории игр , MIT Press, ISBN 978-0-262-65040-3 . Современное введение на уровне выпускников.
Паундстоун, Уильям (1993). Дилемма заключенного (1-е изд. Anchor Books). Нью-Йорк: Якорь. ISBN 0-385-41580-Х .
Куайн, Wvo (1967), «Истина по условностям», Philosophica Essays для А. Н. Уайтхеда , Russel and Russel Publishers, ISBN 978-0-8462-0970-6
Куайн, WvO (1960), «Карнап и логическая истина», Synthese , 12 (4): 350–374, doi : 10.1007/BF00485423 , S2CID 46979744
Скирмс, Брайан (1996), Эволюция общественного договора , Cambridge University Press, ISBN 978-0-521-55583-8
Скирмс, Брайан (2004), Охота на оленя и эволюция социальной структуры , Cambridge University Press, ISBN 978-0-521-53392-8
Трезвый, Эллиотт; Уилсон, Дэвид Слоан (1998), Другим: эволюция и психология бескорыстного поведения , издательство Гарвардского университета, ISBN 978-0-674-93047-6
Уэбб, Джеймс Н. (2007), Теория игр: решения, взаимодействие и эволюция , Бакалавриат по математике, Springer, ISBN 978-1-84628-423-6 Согласованное рассмотрение типов игр, обычно требуемых различными прикладными областями, например, марковскими процессами принятия решений .

Дальнейшее чтение

Учебники и общая литература

Ауманн, Роберт Дж (1987), «Теория игр», The New Palgrave: A Dictionary of Economics , vol. 2, стр. 460–82 .
Камерер, Колин (2003), «Введение» , Теория поведенческих игр: эксперименты в стратегическом взаимодействии , Фонд Рассела Сейджа, стр. 1–25, ISBN 978-0-691-09039-9 , заархивировано из оригинала 14 мая 2011 г. , дата обращения 9 февраля 2011 г. , Описание .
Дутта, Праджит К. (1999), Стратегии и игры: теория и практика , MIT Press , ISBN 978-0-262-04169-0 . Подходит для студентов бакалавриата и бизнеса.
Фернандес, Л.Ф.; Бирман, Х.С. (1998), Теория игр с экономическими приложениями , Аддисон-Уэсли , ISBN 978-0-201-84758-1 . Подходит для студентов старших курсов.
Гаффал, Маргит; Падилья Гальвес, Хесус (2014). Динамика рациональных переговоров: теория игр, языковые игры и формы жизни . Спрингер.
Гиббонс, Роберт Д. (1992), Теория игр для экономистов-прикладников , Princeton University Press, ISBN 978-0-691-00395-5 . Подходит для студентов продвинутого уровня.
- Опубликовано в Европе как Гиббонс, Роберт (2001), Учебник по теории игр , Лондон: Harvester Wheatsheaf, ISBN 978-0-7450-1159-2 .
Гинтис, Герберт (2000), Развитие теории игр: проблемно-ориентированное введение в моделирование стратегического поведения , Princeton University Press, ISBN 978-0-691-00943-8
Грин, Джерри Р.; Мас-Колелл, Андреу ; Уинстон, Майкл Д. (1995), Микроэкономическая теория , Oxford University Press , ISBN 978-0-19-507340-9 . Представляет теорию игр в формальной форме, подходящей для выпускников.
Джозеф Э. Харрингтон (2008) Игры, стратегии и принятие решений , Стоит, ISBN 0-7167-6630-2 . Учебник подходит для магистрантов прикладных направлений; многочисленные примеры, меньше формализмов в изложении концепций.
Айзекс, Руфус (1999), Дифференциальные игры: математическая теория с приложениями к войне и преследованию, контролю и оптимизации , Нью-Йорк: Dover Publications , ISBN 978-0-486-40682-4
Машлер, Майкл; Солан, Эйлон; Замир, Шмуэль (2013), Теория игр , Издательство Кембриджского университета, ISBN 978-1-108-49345-1 . Учебник для бакалавриата.
Миллер, Джеймс Х. (2003), Теория игр в действии: как использовать теорию игр, чтобы перехитрить и перехитрить своих конкурентов , Нью-Йорк: McGraw-Hill , ISBN 978-0-07-140020-6 . Подходит для широкой аудитории.
Шохам, Йоав; Лейтон-Браун, Кевин (2009), Мультиагентные системы: алгоритмические, теоретико-игровые и логические основы , Нью-Йорк: Издательство Кембриджского университета, ISBN 978-0-521-89943-7 , получено 8 марта 2016 г.
Уотсон, Джоэл (2013), Стратегия: введение в теорию игр (3-е издание) , Нью-Йорк: WW Norton and Co., ISBN 978-0-393-91838-0 . Ведущий учебник для продвинутого уровня бакалавриата.
Маккейн, Роджер А. (2010). Теория игр: нетехническое введение в анализ стратегии . Всемирная научная. ISBN 978-981-4289-65-8 .

Исторически важные тексты

Ауманн, Р.Дж. ; Шепли, Л.С. (1974), Ценности неатомных игр , Princeton University Press
Курно, А. Огюстен (1838), «Исследование математических принципов теории богатства», библиотекарь политических и социальных наук.
Эджворт, Фрэнсис Ю. (1881), Математическая экстрасенсорика , Лондон: Кеган Пол
Фаркухарсон, Робин (1969), Теория голосования , Блэквелл (Йельский университет в США), ISBN 978-0-631-12460-3
Люс, Р. Дункан ; Райффа, Ховард (1957), Игры и решения: введение и критический обзор , Нью-Йорк: Wiley

переиздание: Р. Дункан Люс; Говард Райффа (1989), Игры и решения: введение и критический обзор , Нью-Йорк: Dover Publications , ISBN 978-0-486-65943-5

Мейнард Смит, Джон (1982), Эволюция и теория игр , Cambridge University Press, ISBN 978-0-521-28884-2
Нэш, Джон (1950), «Точки равновесия в играх с участием n человек», Труды Национальной академии наук Соединенных Штатов Америки , 36 (1): 48–49, Bibcode : 1950PNAS...36... 48N , doi : 10.1073/pnas.36.1.48 , PMC 1063129 , PMID 16588946
Шепли, Л.С. (1953), Ценность игр с участием n человек, В: Вклад в теорию игр, том II, Х.В. Кун и А.В. Такер (ред.)
Шепли, Л.С. (октябрь 1953 г.). «Стохастические игры» . Труды Национальной академии наук . 39 (10): 1095–1100. Бибкод : 1953PNAS...39.1095S . дои : 10.1073/pnas.39.10.1095 . ПМЦ 1063912 . ПМИД 16589380 .
фон Нейман, Джон (1928), «Zur Theorie der Gesellschaftsspiele», Mathematische Annalen , 100 (1): 295–320, doi : 10.1007/bf01448847 , S2CID 122961988 Английский перевод: «О теории стратегических игр», в AW Такер и Р.Д. Люс, изд. (1959), Вклад в теорию игр , т. 4, с. 42. Издательство Принстонского университета.
фон Нейман, Джон ; Моргенштерн, Оскар (1944), «Теория игр и экономическое поведение» , Nature , 157 (3981), Princeton University Press: 172, Бибкод : 1946Natur.157..172R , doi : 10.1038/157172a0 , S2CID 29754824
Цермело, Эрнст (1913), «О применении теории множеств к теории шахмат», Труды Пятого Международного конгресса математиков , 2 : 501–4.

Другой материал

Аллан Гиббард , «Манипулирование схемами голосования: общий результат», Econometrica , Vol. 41, № 4 (1973), стр. 587–601.
Макдональд, Джон (1950–1996), Стратегия в покере, бизнесе и войне , WW Norton , ISBN 978-0-393-31457-1 . Введение непрофессионала.
Папайоану, Пол (2010), Теория игр для бизнеса: учебник по стратегическим играм , Вероятностный , ISBN 978-0-9647938-7-3 .
Саттертуэйт, Марк Аллен (апрель 1975 г.). «Стратегическая устойчивость и условия Эрроу: теоремы существования и соответствия для процедур голосования и функций социального благосостояния» (PDF) . Журнал экономической теории . 10 (2): 187–217. дои : 10.1016/0022-0531(75)90050-2 .
Зигфрид, Том (2006), Красивая математика , Джозеф Генри Пресс, ISBN 978-0-309-10192-9
Скирмс, Брайан (1990), Динамика рационального обсуждения , издательство Гарвардского университета , ISBN 978-0-674-21885-7

Тралл, Роберт М .; Лукас, Уильям Ф. (1963), " $n$ -личные игры в форме функции распределения», Naval Research Logistics Quarterly , 10 (4): 281–298, doi : 10.1002/nav.3800100126
Долев, Шломи; Панагопулу, Панайота Н.; Раби, Микаэль; Шиллер, Элад М.; Спиракис, Пол Г. (2011). «Авторитет рациональности для доказуемого рационального поведения» . Материалы 30-го ежегодного симпозиума ACM SIGACT-SIGOPS по принципам распределенных вычислений . стр. 289–290. дои : 10.1145/1993806.1993858 . ISBN 978-1-4503-0719-2 .
Честейн, Эрик; Ливнат, Ади; Пападимитриу, Христос ; Вазирани, Умеш (июнь 2014 г.), «Алгоритмы, игры и эволюция», Proceedings of the National Academy of Sciences of the United States of America , 111 (29): 10620–10623, Bibcode : 2014PNAS..11110620C , doi : 10.1073 /pnas.1406556111 , PMC 4115542 , PMID 24979793

Внешние ссылки

Джеймс Миллер (2015): Вводные видеоролики по теории игр .
«Игры, теория» , Энциклопедия математики , EMS Press , 2001 [1994]
Пол Уокер: Страница истории теории игр .
Дэвид Левин: Теория игр. Статьи, конспекты лекций и многое другое.
Элвин Рот: «Страница теории игр и экспериментальной экономики» . Архивировано из оригинала 15 августа 2000 года . Проверено 13 сентября 2003 г. — Полный список ссылок на информацию по теории игр в Интернете.
Адам Калай: Теория игр и информатика - Конспекты лекций по теории игр и информатике
Майк Шор: GameTheory.net — конспекты лекций, интерактивные иллюстрации и другая информация.
Джима Рэтлиффа Аспирантура по теории игр (конспекты лекций).
Дон Росс: Обзор теории игр в Стэнфордской энциклопедии философии .
Бруно Вербек и Кристофер Моррис: теория игр и этика
Элмер Г. Винс: Теория игр — Введение, рабочие примеры, онлайн-игры для двух человек с нулевой суммой.
Марек М. Камински: Теория игр и политика. Архивировано 20 октября 2006 г. в Wayback Machine — учебные программы и конспекты лекций по теории игр и политологии.
Веб-сайты по теории игр и социальным взаимодействиям
Кестена Грина Прогнозирование конфликтов с помощью Wayback Machine (архивировано 11 апреля 2011 г.) — доказательства точности прогнозов на основе теории игр и других методов см. . в статьях Архивировано 15 сентября 2019 г. в Wayback Machine .
МакКелви, Ричард Д., МакЛеннан, Эндрю М. и Туроци, Теодор Л. (2007) Гамбит: программные инструменты для теории игр .
Бенджамин Полак: Открытый курс теории игр в Йельском университете. Архивировано 3 августа 2010 г., на Wayback Machine . видео курса
Бенджамин Мориц, Бернхард Кёнсген, Дэнни Бурес, Ронни Вирш, (2007) Spieltheorie-Software.de: Приложение для теории игр, реализованное на JAVA .
Антонин Кучера: Стохастические игры для двух игроков .
Ю-Чи Хо: Что такое математическая теория игр ; Что такое математическая теория игр (№ 2) ; Что такое математическая теория игр (№3) ; Что такое математическая теория игр (№ 4) — Теория игр для многих людей ; Что такое математическая теория игр? (#5) – Финал, подведение итогов и мое мнение

[17] Хотя общеизвестные знания были впервые обсуждены философом Дэвидом Льюисом в его диссертации (а затем и книге) «Конвенция» в конце 1960-х годов, экономисты не рассматривали их широко до Роберта Ауманна в 1970-х годах. работы

[76] Экспериментальная работа в теории игр имеет много названий: экспериментальная экономика , поведенческая экономика и поведенческая теория игр . ^[74]

[78] В JEL: C7 классификационных кодов Журнала экономической литературы .

[143] Более подробное обсуждение использования теории игр в этике см. в Стэнфордской энциклопедии философии вступительной теории игр и этики .

[Myerson-1] Перейти обратно: ^а ^б Майерсон, Роджер Б. (1991). Теория игр: анализ конфликта . Издательство Гарвардского университета . ISBN 9780674341166 .

[2] Шепли, Ллойд С.; Шубик, Мартин (1 января 1971 г.). «Глава 1, Введение, Использование моделей». Теория игр в экономике . Архивировано из оригинала 23 апреля 2023 года . Проверено 23 апреля 2023 г.

[3] Нойманн, Джон фон; Моргенштерн, Оскар (8 апреля 2007 г.). Теория игр и экономического поведения . Издательство Принстонского университета. ISBN 978-0-691-13061-3 . Архивировано из оригинала 28 марта 2023 года . Проверено 23 апреля 2023 г.

[4] Нисан (2020). «Отчет о книге: Теория игр и экономического поведения (фон Нейман и Моргенштерн)» . lesswrong.com .

[5] Хан, Фейсал Шах; Солмейер, Нил; Балу, Радхакришнан; Скромный, Трэвис С. (ноябрь 2018 г.). «Квантовые игры: обзор истории, современное состояние и интерпретация». Квантовая обработка информации . 17 (11): 309. Бибкод : 2018QuIP...17..309К . дои : 10.1007/s11128-018-2082-8 .

[6] Мартин, Брайан (1978). «Избирательная полезность теории игр». Социальные исследования науки . 8 (1): 85–110. дои : 10.1177/030631277800800103 . JSTOR 284857 . Тем не менее, математические методы, используемые в теории игр, направлены на достижение единственной цели: максимизация «уровня безопасности», где уровень безопасности — это наименьшая сумма, которую игрок может получить от выбора стратегии.

[7] Шафер, Г. (2018, декабрь). Теоретико-игровые основы вероятности Паскаля и Гюйгенса . Лекция Сартона, Школа архитектуры и инженерии, Гентский университет. [1]

[GT-PD-01-8] Беллхаус, Дэвид Р. (2007), «Проблема Уолдегрейва» (PDF) , Journal Électronique d'Histoire des Probabilités et de la Statistique [ Электронный журнал истории вероятностей и статистики ], 3 (2), в архиве (PDF) с сайта оригинал от 20 августа 2008 г.

[9] Беллхаус, Дэвид Р. (2015). «Ле Хер и другие проблемы вероятности, обсуждаемые Бернулли, Монмором и Уолдегрейвом». Статистическая наука . 30 (1). Институт математической статистики : 26–39. arXiv : 1504.01950 . Бибкод : 2015arXiv150401950B . дои : 10.1214/14-STS469 . S2CID 59066805 .

[10] Цермело, Эрнст (1913). Хобсон, EW; Любовь, AEH (ред.). Über eine Anwendung der Mengenlehre auf die Theorie des Schachspiels [ О применении теории множеств к теории игры в шахматы ] (PDF) . Труды Пятого Международного конгресса математиков (1912 г.) (на немецком языке). Кембридж: Издательство Кембриджского университета. стр. 501–504. Архивировано из оригинала (PDF) 31 июля 2020 года . Проверено 29 августа 2019 г.

[11] Ким, Сунгук, изд. (2014). Применение теории игр в сетевом проектировании . IGI Global. п. 3. ISBN 978-1-4666-6051-9 .

[12] фон Нейман, Джон (1928). «К теории игр стратегии». Математические Анналы [ Mathematical Annals ] (на немецком языке). 100 (1): 295–320. дои : 10.1007/BF01448847 . S2CID 122961988 .

[13] фон Нейман, Джон (1959). «К теории игр-стратегий» . В Такере, штат Аризона; Люси, Р.Д. (ред.). Вклад в теорию игр . Том. 4. Перевод Баргманна, Сони. Принстон, Нью-Джерси : Издательство Принстонского университета . стр. 13–42. ISBN 0-691-07937-4 .

[14] Мировский, Филип (1992). «Чего пытались достичь фон Нейман и Моргенштерн?» . В Вайнтраубе, Э. Рой (ред.). К истории теории игр . Дарем: Издательство Университета Дьюка. стр. 113–147. ISBN 978-0-8223-1253-6 .

[15] Леонард, Роберт (2010), Фон Нейман, Моргенштерн и создание теории игр , Нью-Йорк: Издательство Кембриджского университета, номер документа : 10.1017/CBO9780511778278 , ISBN 978-0-521-56266-9

[stanfordprisoner-16] Кун, Стивен (4 сентября 1997 г.). Залта, Эдвард Н. (ред.). «Дилемма заключенного» . Стэнфордская энциклопедия философии . Стэнфордский университет. Архивировано из оригинала 18 января 2012 года . Проверено 3 января 2013 г.

[18] Шор, Майк. «Некооперативная игра» . GameTheory.net . Архивировано из оригинала 1 апреля 2014 года . Проверено 15 сентября 2016 г.

[19] Чандрасекаран, Рамасвами. «Теория кооперативных игр» (PDF) . Техасский университет в Далласе. Архивировано (PDF) из оригинала 18 апреля 2016 г.

[20] Бранденбургер, Адам. «Теория кооперативных игр: характеристические функции, распределение, предельный вклад» (PDF) . Архивировано из оригинала (PDF) 29 августа 2017 года . Проверено 14 апреля 2020 г.

[21] Шор, Майк (2006). «Симметричная игра» . Теория игр.net .

[22] Оуэн, Гильермо (1995). Теория игр: Третье издание . Бингли: Издательство Emerald Group. п. 11. ISBN 978-0-12-531151-9 .

[23] Чанг, Куан-Хуа (2015). «Решения в инженерном проектировании». Теория проектирования и методы с использованием CAD/CAE . стр. 39–101. дои : 10.1016/b978-0-12-398512-5.00002-5 . ISBN 978-0-12-398512-5 .

[:2-24] Перейти обратно: ^а ^б ^с ^д ^и Гиббонс, Роберт (1992). Теория игр для экономистов-прикладников . Принстон, Нью-Джерси: Издательство Принстонского университета. стр. 14–17. ISBN 0-691-04308-6 .

[25] Фергюсон, Томас С. «Теория игр» (PDF) . Математический факультет Калифорнийского университета в Лос-Анджелесе. стр. 56–57. Архивировано (PDF) из оригинала 30 июля 2004 г.

[26] Мысельский, Ян (1992). «Игры с совершенной информацией». Справочник по теории игр с экономическими приложениями . Том. 1. С. 41–70. дои : 10.1016/S1574-0005(05)80006-2 . ISBN 978-0-4448-8098-7 .

[27] «Бесконечные шахматы» . Бесконечный сериал PBS . 2 марта 2017 г. Архивировано из оригинала 28 октября 2021 г. Совершенная информация определена в 0:25, с академическими источниками arXiv : 1302.4377 и arXiv : 1510.08155 .

[28] Оуэн, Гильермо (1995). Теория игр: Третье издание . Бингли: Издательство Emerald Group. п. 4. ISBN 978-0-12-531151-9 .

[29] Мирман, Леонард Дж. (1989). «Идеальная информация». Теория игр . стр. 194–198. дои : 10.1007/978-1-349-20181-5_22 . ISBN 978-0-333-49537-7 .

[30] Мирман, Леонард (1989). Совершенная информация . Лондон: Пэлгрейв Макмиллан. стр. 194–195. ISBN 978-1-349-20181-5 .

[FOOTNOTEShohamLeyton-Brown200860-31] Шохам и Лейтон-Браун (2008) , с. 60.

[32] Осборн, Мартин Дж. (2000). Введение в теорию игр . Издательство Оксфордского университета. стр. 271–272.

[33] Осборн, Мартин Дж (2020). Введение в теорию игр . Издательство Оксфордского университета. стр. 271–277.

[Bewersdorff2005-34] Перейти обратно: ^а ^б Йорг Беверсдорф (2005). «31». Удача, логика и белая ложь: математика игр . AK Peters, Ltd., стр. ix–xii. ISBN 978-1-56881-210-6 .

[35] Альберт, Майкл Х .; Новаковски, Ричард Дж.; Вулф, Дэвид (2007), Уроки игры: введение в комбинаторную теорию игр , AK Peters Ltd, стр. 3–4, ISBN 978-1-56881-277-9

[36] Бек, Йожеф (2008). Комбинаторные игры: теория крестиков-ноликов . Издательство Кембриджского университета. стр. 1–3 . ISBN 978-0-521-46100-9 .

[37] Хирн, Роберт А.; Демейн, Эрик Д. (2009), Игры, головоломки и вычисления , AK Peters, Ltd., ISBN 978-1-56881-322-6

[Jones2008-38] Джонс, М. Тим (2008). Искусственный интеллект: системный подход . Джонс и Бартлетт Обучение. стр. 106–118. ISBN 978-0-7637-7337-3 .

[PM66-39] Петросян, Луизиана; Мурзов, Н. В. (1966). «Теоретико-игровые задачи механики». Литовск. Мат. Сб. (на русском языке). 6 : 423–433.

[Newton2018renaissance-40] Ньютон, Джонатан (2018). «Эволюционная теория игр: Возрождение» . Игры . 9 (2): 31. дои : 10.3390/g9020031 . hdl : 10419/179191 .

[FOOTNOTEWebb2007-41] Уэбб (2007) .

[42] Лозовану, Д; Пикл, С (2015). Теоретико-игровой подход к марковским процессам принятия решений, стохастическим позиционным играм и моделям многокритериального управления . Спрингер, Чам. ISBN 978-3-319-11832-1 .

[FOOTNOTEOsborneRubinstein1994-43] Осборн и Рубинштейн (1994) .

[McMahan-44] Перейти обратно: ^а ^б МакМахан, Хью Брендан (2006). Надежное планирование в областях со стохастическими результатами, противниками и частичной наблюдаемостью (PDF) (кандидатская диссертация). Университет Карнеги-Меллон. стр. 3–4. Архивировано (PDF) из оригинала 1 апреля 2011 г.

[FOOTNOTEHoward1971-45] Ховард (1971) .

[r7a-46] Перейти обратно: ^а ^б Расмусен, Эрик (2007). Игры и информация (4-е изд.). Уайли. ISBN 978-1-4051-3666-2 .

[r7b-47] Перейти обратно: ^а ^б Крепс, Дэвид М. (1990). Теория игр и экономическое моделирование . Издательство Оксфордского университета. дои : 10.1093/0198283814.001.0001 . ISBN 978-0-19-828381-2 . ^{[ нужна страница ]}

[r7c-48] Перейти обратно: ^а ^б Ауманн, Р.Дж.; Харт, С., ред. (1992). Справочник по теории игр с экономическими приложениями . Эльзевир. ISBN 978-0-444-89427-4 . ^{[ нужна страница ]}

[r7d-49] Перейти обратно: ^а ^б Ауманн, Роберт Дж.; Хейфец, Авиад (2002). «Глава 43 Неполная информация». Справочник по теории игр с экономическими приложениями, том 3 . Том. 3. стр. 1665–1686. дои : 10.1016/S1574-0005(02)03006-0 . ISBN 978-0-444-89428-1 .

[50] Фуденберг, Дрю; Тироль, Жан (1991). Теория игр . С Прессой. п. 67. ИСБН 978-0-262-06141-4 .

[51] Уильямс, Пол Д. (2013). Исследования безопасности: введение (второе изд.). Абингдон : Рутледж. стр. 55–56.

[FOOTNOTEShohamLeyton-Brown200835-52] Шохам и Лейтон-Браун (2008) , с. 35.

[53] $2^{N}$ обозначает мощности набор $N$ .

[54] Тагиев, Рустам (3 мая 2011 г.). «Если для прогнозирования стратегического взаимодействия реальных агентов необходимо нечто большее, чем аналитическое моделирование». arXiv : 1105.0558 [ cs.GT ].

[55] Розенталь, Роберт В. (декабрь 1973 г.). «Класс игр, обладающих чисто стратегическим равновесием Нэша». Международный журнал теории игр . 2 (1): 65–67. дои : 10.1007/BF01737559 . S2CID 121904640 .

[56] Коллер, Дафна ; Мегиддо, Нимрод ; фон Стенгель, Бернхард (1994). «Быстрые алгоритмы поиска рандомизированных стратегий в деревьях игр». Материалы двадцать шестого ежегодного симпозиума ACM по теории вычислений – STOC '94 . стр. 750–759. дои : 10.1145/195058.195451 . ISBN 0-89791-663-8 . S2CID 1893272 .

[57] Алур, Раджив; Дилл, Дэвид Л. (апрель 1994 г.). «Теория синхронизированных автоматов» . Теоретическая информатика . 126 (2): 183–235. дои : 10.1016/0304-3975(94)90010-8 .

[58] Томлин, CJ; Лигерос, Дж.; Шанкар Шастри, С. (июль 2000 г.). «Теоретико-игровой подход к проектированию контроллеров для гибридных систем». Труды IEEE . 88 (7): 949–970. дои : 10.1109/5.871303 . S2CID 1844682 .

[59] Коллер, Дафна; Пфеффер, Ави (июль 1997 г.). «Представления и решения теоретико-игровых задач». Искусственный интеллект . 94 (1–2): 167–215. дои : 10.1016/S0004-3702(97)00023-4 .

[60] Майкл, Майкл Кернс; Литтман, Майкл Л. (2001). «Графические модели для теории игр». В УАИ : 253–260. CiteSeerX 10.1.1.22.5705 .

[61] Кернс, Майкл; Литтман, Майкл Л.; Сингх, Сатиндер (7 марта 2011 г.). «Графические модели для теории игр». arXiv : 1301.2281 [ cs.GT ].

[62] Лейтон Браун, Кевин; Тенненхольц, Моше (2005). Игры с локальными эффектами (PDF) . Материалы семинара Дагштуля. Центр компьютерных наук замка Дагштуль-Лейбница . Проверено 3 февраля 2023 г.

[63] Генесерет, Михаил; С любовью, Натаниэль; Пелл, Барни (15 июня 2005 г.). «Общая игра: обзор соревнований AAAI». Журнал ИИ . 26 (2): 62. дои : 10.1609/aimag.v26i2.1813 .

[64] Клемпнер, Хулио (2006). «Моделирование игр по кратчайшему пути с помощью сетей Петри: теория, основанная на Ляпунове» . Международный журнал прикладной математики и информатики . 16 (3): 387–397.

[65] Санников, Юлий (сентябрь 2007 г.). «Игры с несовершенно наблюдаемыми действиями в непрерывном времени» (PDF) . Эконометрика . 75 (5): 1285–1329. дои : 10.1111/j.1468-0262.2007.00795.x .

[66] Тагиев, Рустам (декабрь 2008 г.). «Мультиагентные игры Петри». 2008 Международная конференция по вычислительному интеллекту для моделирования управления и автоматизации . стр. 130–135. дои : 10.1109/CIMCA.2008.15 . ISBN 978-0-7695-3514-2 . S2CID 16679934 .

[67] Тагиев, Рустам (2009). «О многоагентных моделях сетей Петри для вычисления обширных конечных игр». Новые вызовы в области вычислительного коллективного разума . Исследования в области вычислительного интеллекта. Том. 244. Спрингер. стр. 243–254. дои : 10.1007/978-3-642-03958-4_21 . ISBN 978-3-642-03957-7 .

[68] Бхат, Навин; Лейтон-Браун, Кевин (11 июля 2012 г.). «Вычисление равновесия Нэша в играх с графом действий». arXiv : 1207.4128 [ cs.GT ].

[Larson-69] Ларсон, Дженнифер М. (11 мая 2021 г.). «Сети конфликта и сотрудничества» . Ежегодный обзор политической науки . 24 (1): 89–107. doi : 10.1146/annurev-polisci-041719-102523 .

[70] Фридман, Дэниел (1998). «Об экономических применениях эволюционной теории игр» (PDF) . Журнал эволюционной экономики . 8 : 14–53. Архивировано (PDF) из оригинала 11 февраля 2014 года.

[Camerer2003-71] Перейти обратно: ^а ^б Камерер, Колин Ф. (2003). «1.1 Для чего нужна теория игр?». Поведенческая теория игр: эксперименты по стратегическому взаимодействию . стр. 5–7. Архивировано из оригинала 14 мая 2011 года.

[72] Браун, Будевейн де (сентябрь 2005 г.). «Теория игр в философии». Топои . 24 (2): 197–208. дои : 10.1007/s11245-005-5055-3 .

[73] Росс, Дон (10 марта 2006 г.). «Теория игр» . В Залте, Эдвард Н. (ред.). Стэнфордская энциклопедия философии . Стэнфордский университет . Проверено 21 августа 2008 г.

[74] Велегол, Даррелл; Сухи, Пол; Коннолли, Джон; Моррисси, Натали; Кук, Лаура (17 октября 2018 г.). «Химическая теория игр». Исследования в области промышленной и инженерной химии . 57 (41): 13593–13607. doi : 10.1021/acs.iecr.8b03835 . S2CID 105204747 .

[75] Камерер, Колин Ф. (2003). "Введение". Поведенческая теория игр: эксперименты по стратегическому взаимодействию . стр. 1–25. Архивировано из оригинала 14 мая 2011 года.

[77] Кадане, Джозеф Б.; Ларки, Патрик Д. (декабрь 1983 г.). «Путаница того, что есть и что должно быть в контексте теории игр». Наука управления . 29 (12): 1365–1379. дои : 10.1287/mnsc.29.12.1365 .

[79] Ауманн, Роберт Дж. (2008). «теория игр» . Новый экономический словарь Пэлгрейва (2-е изд.). Архивировано из оригинала 15 мая 2011 года . Проверено 22 августа 2011 г.

[80] Шубик, Мартин (1981). «Модели и методы теории игр в политической экономии». В «Стреле», Кеннет ; Интрилигатор, Майкл (ред.). Справочник по математической экономике, т. 1 . 1. Том. 1. С. 285–330. дои : 10.1016/S1573-4382(81)01011-4 . ISBN 978-0-444-86126-9 .

[81] Шапиро, Карл (весна 1989 г.). «Теория бизнес-стратегии». Экономический журнал RAND . 20 (1). Уайли : 125–137. JSTOR 2555656 . ПМИД 10296625 . .

[GT-A-E-00-82] Агарвал, Н.; Зеефонгсекул, П. (11–12 декабря 2011 г.). Психологическое ценообразование в слияниях и поглощениях с использованием теории игр (PDF) . 19-й Международный конгресс по моделированию и симуляции . Перт . Проверено 3 февраля 2023 г.

[83] Тесфацион, Ли (2006). Агентно-ориентированная вычислительная экономика: конструктивный подход к экономической теории . Справочник по вычислительной экономике. Том. 2. стр. 831–880. дои : 10.1016/S1574-0021(05)02016-2 . ISBN 978-0-444-51253-6 .

[84] Джозеф Ю. Халперн (2008). «Информатика и теория игр» . Новый экономический словарь Пэлгрейва .

[85] Майерсон, Роджер Б. (2008). «конструкция механизма» . Новый экономический словарь Пэлгрейва . Архивировано из оригинала 23 ноября 2011 года . Проверено 4 августа 2011 г.

[86] Майерсон, Роджер Б. (2008). «принцип откровения» . Новый экономический словарь Пэлгрейва . Архивировано из оригинала 16 мая 2013 года . Проверено 4 августа 2011 г.

[87] Сандхольм, Туомас (2008). «Компьютинг в проектировании механизмов» . Новый экономический словарь Пэлгрейва . Архивировано из оригинала 23 ноября 2011 года . Проверено 5 декабря 2011 г.

[nisanronen2001-88] Перейти обратно: ^а ^б Нисан, Ноам; Ронен, Амир (апрель 2001 г.). «Проектирование алгоритмических механизмов». Игры и экономическое поведение . 35 (1–2): 166–196. дои : 10.1006/game.1999.0790 .

[nisan2007-89] Перейти обратно: ^а ^б Нисан, Ноам ; Рафгарден, Тим; Тардос, Ева; Вазирани, Виджай В., ред. (2007). Алгоритмическая теория игр . Издательство Кембриджского университета . ISBN 9780521872829 . LCCN 2007014231 .

[90] Брамс, Стивен Дж. (1994). Глава 30. Порядок голосования . Справочник по теории игр с экономическими приложениями. Том. 2. С. 1055–1089. дои : 10.1016/S1574-0005(05)80062-1 . ISBN 978-0-444-89427-4 . и Мулен, Эрве (1994). Глава 31 Социальный выбор . Справочник по теории игр с экономическими приложениями. Том. 2. С. 1091–1125. дои : 10.1016/S1574-0005(05)80063-3 . ISBN 978-0-444-89427-4 .

[91] Смит, Вернон Л. (декабрь 1992 г.). «Теория игр и экспериментальная экономика: начало и ранние влияния». История политической экономии . 24 (Приложение): 241–282. doi : 10.1215/00182702-24-Supplement-241 .

[92] Смит, Вернон Л. (2001). «Экспериментальная экономика». Международная энциклопедия социальных и поведенческих наук . стр. 5100–5108. дои : 10.1016/B0-08-043076-7/02232-4 . ISBN 978-0-08-043076-8 .

[93] Плотт, Чарльз Р.; Смит, Вернон Л., ред. (2008). Справочник результатов экспериментальной экономики . Эльзевир. ISBN 978-0-08-088796-8 . ^{[ нужна страница ]}

[94] Винсент П. Кроуфорд (1997). «Теория и эксперимент в анализе стратегического взаимодействия», в журнале «Достижения в области экономики и эконометрики: теория и приложения» , стр. 206–242. Архивировано 1 апреля 2012 г. в Wayback Machine . Кембридж. Перепечатано в книге Колина Ф. Камерера и др ., изд. (2003). Достижения поведенческой экономики , Принстон. Статьи 1986–2003 гг. Описание Архивировано 18 января 2012 года в Wayback Machine , предварительный просмотр , Принстон, гл. 12

[95] Шубик, Мартин (2002). «Глава 62 Теория игр и экспериментальные игры». Справочник по теории игр с экономическими приложениями, том 3 . Том. 3. С. 2327–2351. дои : 10.1016/S1574-0005(02)03025-4 . ISBN 978-0-444-89428-1 .

[96] Новый экономический словарь Пэлгрейва . 2008. Фарук Гюль . «Поведенческая экономика и теория игр». Абстрактный. Архивировано 7 августа 2017 года в Wayback Machine.

[97] Камерер, Колин Ф. (2008). «Поведенческая теория игр» . Новый экономический словарь Пэлгрейва . Архивировано из оригинала 23 ноября 2011 года . Проверено 4 августа 2011 г.

[98] Камерер, Колин Ф. (1997). «Прогресс в поведенческой теории игр» . Журнал экономических перспектив . 11 (4): 172. doi : 10.1257/jep.11.4.167 .

[99] Камерер, Колин Ф. (2003). Поведенческая теория игр . Принстон. Описание. Архивировано 14 мая 2011 г. в Wayback Machine , предварительный просмотр. Архивировано 26 марта 2023 г. в Wayback Machine ([ctrl]+), и гл. 1 ссылка. Архивировано 4 июля 2013 г. на Wayback Machine .

[100] Камерер, Колин Ф.; Левенштейн, Джордж; Рабин, Мэтью, ред. (2011). Достижения в поведенческой экономике . Издательство Принстонского университета. ISBN 978-1-4008-2911-8 . ^{[ нужна страница ]}

[101] Фуденберг, Дрю (2006). «Продвижение за пределы достижений поведенческой экономики» . Журнал экономической литературы . 44 (3): 694–711. дои : 10.1257/jel.44.3.694 . JSTOR 30032349 . S2CID 3490729 .

[102] Тироль, Жан (1988). Теория промышленной организации . МТИ Пресс. Описание и ссылки на предварительный просмотр глав, стр. vii–ix , «Общая организация», стр. 5–6 , и «Теория некооперативных игр: Руководство пользователя», гл. 11, стр. 423–59 .

[103] Бэгвелл, Кайл; Волински, Ашер (2002). «Теория игр и промышленная организация». Справочник по теории игр с экономическими приложениями, том 3 . Том. 3. стр. 1851–1895. дои : 10.1016/S1574-0005(02)03012-6 . ISBN 978-0-444-89428-1 .

[104] Фелс, Э.М. (1961). «Обзор стратегии и структуры рынка: конкуренция, олигополия и теория игр». Архив Weltwirtschaftliches . 87 : 12–14. JSTOR 40434883 .

[105] Рид, Гэвин К. (1982). «Обзор структуры и поведения рынка». Экономический журнал . 92 (365): 200–202. дои : 10.2307/2232276 . JSTOR 2232276 .

[106] Мартин Шубик (1981). «Модели и методы теории игр в политической экономии», в « Справочнике по математической экономике» , т. 1, стр. 285–330. два : 10.1016/S1573-4382(81)01011-4 .

[107] Мартин Шубик (1987). Теоретико-игровой подход к политической экономии . МТИ Пресс. Описание . Архивировано 29 июня 2011 года в Wayback Machine.

[108] Мартин Шубик (1978). «Теория игр: экономические приложения», в изд. В. Крускала и Дж. М. Танура, Международная энциклопедия статистики , т. 2, стр. 372–78.

[109] Ауманн, Р.Дж.; Харт, С., ред. (1992). Справочник по теории игр с экономическими приложениями . Эльзевир. ISBN 978-0-444-89427-4 . ^{[ нужна страница ]}

[GT-F-R-09-110] Кристен, Маркус (1 июля 1998 г.). «Теоретико-игровая модель для изучения двух компромиссов при получении информации для тщательного балансирования» . ИНСЕАД . Архивировано из оригинала 24 мая 2013 года . Проверено 1 июля 2012 года .

[GT-F-R-10-111] Шевалье-Руаньян, Бенуа; Тригеоргис, Ленос (15 февраля 2012 г.). «Игры с опционами: баланс между гибкостью и обязательностью» . Европейский финансовый обзор . Архивировано из оригинала 20 июня 2013 года . Проверено 3 января 2013 г.

[112] Уилкинсон, Ник (2005). «Теория игр». Управленческая экономика . стр. 331–381. дои : 10.1017/CBO9780511810534.015 . ISBN 978-0-521-81993-0 .

[113] «Партнеры CIPS и TWS продвигают теорию игр на мировой арене» . 27 ноября 2020 г. Архивировано из оригинала 27 ноября 2020 г. . Проверено 20 апреля 2023 г.

[114] CIPS (2021), Теория игр. Архивировано 11 апреля 2021 г. на Wayback Machine , CIPS совместно с TWS Partners, по состоянию на 11 апреля 2021 г.

[Piraveenan_2019-115] Перейти обратно: ^а ^б Пиравинан, Махендра (2019). «Применение теории игр в управлении проектами: структурированный обзор и анализ» . Математика . 7 (9): 858. doi : 10.3390/math7090858 .

[116] «Что теория игр говорит нам о политике и обществе» . Новости Массачусетского технологического института | Массачусетский технологический институт . 4 декабря 2018 г. Архивировано из оригинала 23 апреля 2023 г. Проверено 23 апреля 2023 г.

[FOOTNOTEDowns1957-117] Даунс (1957) .

[118] Брамс, Стивен Дж. (1 января 2001 г.). «Теория игр и Карибский кризис» . Плюс журнал . Архивировано из оригинала 24 апреля 2015 года . Проверено 31 января 2016 г.

[119] «Как теория игр объясняет «иррациональное» поведение» . Массачусетский технологический институт Слоана . Архивировано из оригинала 23 апреля 2023 года . Проверено 23 апреля 2023 г.

[120] Леви, Гилат; Разин, Ронни (март 2004 г.). «Требуются двое: объяснение демократического мира» . Журнал Европейской экономической ассоциации . 2 (1): 1–29. дои : 10.1162/154247604323015463 .

[121] Фирон, Джеймс Д. (1 января 1995 г.). «Рационалистические объяснения войны». Международная организация . 49 (3): 379–414. дои : 10.1017/s0020818300033324 . JSTOR 2706903 . S2CID 38573183 .

[122] Вуд, Питер Джон (февраль 2011 г.). «Изменение климата и теория игр» . Анналы Нью-Йоркской академии наук . 1219 (1): 153–170. Бибкод : 2011NYASA1219..153W . дои : 10.1111/j.1749-6632.2010.05891.x . ПМИД 21332497 .

[:3-123] Перейти обратно: ^а ^б ^с Хо, Эдвин; Раджагопалан, Арвинд; Скворцов, Алексей; Арулампалам, Санджив; Пиравинан, Махендра (28 января 2022 г.). «Теория игр в оборонных приложениях: обзор» . Датчики . 22 (3): 1032. arXiv : 2111.01876 . Бибкод : 2022Senso..22.1032H . дои : 10.3390/s22031032 . ПМЦ 8838118 . ПМИД 35161778 .

[FOOTNOTEHarperMaynard_Smith2003-124] Харпер и Мейнард Смит (2003) .

[125] Мейнард Смит, Джон (1974). «Теория игр и эволюция конфликтов животных» (PDF) . Журнал теоретической биологии . 47 (1): 209–221. Бибкод : 1974JThBi..47..209M . дои : 10.1016/0022-5193(74)90110-6 . ПМИД 4459582 .

[stan-egt-126] Александр, Дж. Маккензи (19 июля 2009 г.). «Эволюционная теория игр» . В Залте, Эдвард Н. (ред.). Стэнфордская энциклопедия философии . Стэнфордский университет . Проверено 3 января 2013 г.

[qudzyh-127] Перейти обратно: ^а ^б Окаша, Самир (3 июня 2003 г.). «Биологический альтруизм» . В Залте, Эдвард Н. (ред.). Стэнфордская энциклопедия философии . Стэнфордский университет . Проверено 3 января 2013 г.

[ShohamLeyton-Brown2008-128] Шохам, Йоав; Лейтон-Браун, Кевин (2008). Мультиагентные системы: алгоритмические, теоретико-игровые и логические основы . Издательство Кембриджского университета. ISBN 978-1-139-47524-2 . ^{[ нужна страница ]}

[FOOTNOTEBen-DavidBorodinKarpTardos1994-129] Бен-Дэвид и др. (1994) .

[130] Халперн, Джозеф Ю. (2008). «Информатика и теория игр». Новый экономический словарь Пэлгрейва (2-е изд.).

[131] Шохам, Йоав (август 2008 г.). «Информатика и теория игр». Коммуникации АКМ . 51 (8): 74–79. дои : 10.1145/1378704.1378721 .

[132] Литтман, Эми; Литтман, Майкл Л. (2007). «Введение в специальный выпуск по обучению и вычислительной теории игр» . Машинное обучение . 67 (1–2): 3–6. дои : 10.1007/s10994-007-0770-1 . S2CID 22635389 .

[133] Скирмс (1996)

[FOOTNOTEGrimKokalisAlai-TaftiKilb2004-134] Грим и др. (2004) .

[135] Ульманн-Маргалит, Э. (1977), Появление норм , Oxford University Press, ISBN 978-0-19-824411-0 ^{[ нужна страница ]}

[136] Биккьери, Кристина (2006), Грамматика общества: природа и динамика социальных норм , Cambridge University Press, ISBN 978-0-521-57372-6 ^{[ нужна страница ]}

[137] Биккьери, Кристина (1989). «Самоопровергающие теории стратегического взаимодействия: парадокс общеизвестных». Эркеннтнис . 30 (1–2): 69–85. дои : 10.1007/BF00184816 . S2CID 120848181 .

[138] Биккьери, Кристина (1993), Рациональность и координация , издательство Кембриджского университета , ISBN 978-0-521-57444-0

[139] Скирмс, Брайан (1990), Динамика рационального обсуждения , издательство Гарвардского университета, ISBN 978-0-674-21885-7

[140] Сталнакер, Роберт (октябрь 1996 г.). «Знания, убеждения и контрфактические рассуждения в играх». Экономика и философия . 12 (2): 133–163. дои : 10.1017/S0266267100004132 .

[141] Брейтуэйт, Ричард Беван (1955). Теория игр как инструмент философа-моралиста. Вступительная лекция, прочитанная в Кембридже 2 декабря 1954 года . Университетское издательство. ISBN 978-0-521-11351-9 . ^{[ нужна страница ]}

[142] Кун, Стивен Т. (июль 2004 г.). «Размышления об этике и теории игр». Синтезируйте . 141 (1): 1–44. дои : 10.1023/B:SYNT.0000035846.91195.cb .

[144] Чанг, Шерил Л.; Пиравинан, Махендра; Паттисон, Филиппа; Прокопенко, Михаил (2020). «Теоретико-игровое моделирование динамики инфекционных заболеваний и методы вмешательства: обзор». Журнал биологической динамики . 14 (1): 57–89. arXiv : 1901.04143 . Бибкод : 2020JBioD..14...57C . дои : 10.1080/17513758.2020.1720322 . ПМИД 31996099 .

[145] Робертс, Шивон (20 декабря 2020 г.). « Игра «Пандемия — это дилемма узника» » . Нью-Йорк Таймс .

[146] Хэнли, Джон Т. (14 декабря 2021 г.). «ИГРЫ, теория игр и искусственный интеллект» . Журнал оборонной аналитики и логистики . 5 (2): 114–130. дои : 10.1108/JDAL-10-2021-0011 .

[147] Альбрехт, Стефано В.; Кристианос, Филиппос; Шефер, Люк (2024). Многоагентное обучение с подкреплением: основы и современные подходы . С Прессой. ISBN 978-0-262-04937-5 . ^{[ нужна страница ]}

[148] Парашар, Нилеш (15 августа 2022 г.). «Что такое теория игр в ИИ?» . Середина .

[149] Хазра, Танмой; Анджария, Кушал (март 2022 г.). «Применение теории игр в глубоком обучении: обзор» . Мультимедийные инструменты и приложения . 81 (6): 8963–8994. дои : 10.1007/s11042-022-12153-2 . ПМК 9039031 . ПМИД 35496996 .

[FOOTNOTEPoundstone19938,_117-150] Паундстоун 1993 , стр. 8, 117.

[151] Рапопорт, Анатолий (1987). «Дилемма заключенного». Новый экономический словарь Пэлгрейва . стр. 1–5. дои : 10.1057/978-1-349-95121-5_1850-1 . ISBN 978-1-349-95121-5 .

[152] «Битва полов | История, участники и факты | Британника» . www.britanica.com . Архивировано из оригинала 23 апреля 2023 года . Проверено 23 апреля 2023 г.

[153] Атенариум (12 августа 2020 г.). «Битва полов – равновесие Нэша в смешанных стратегиях координации» . Атенариум . Архивировано из оригинала 23 апреля 2023 года . Проверено 23 апреля 2023 г.

[154] Харсаньи, Джон К. (июнь 1961 г.). «О постулатах рациональности, лежащих в основе теории кооперативных игр». Журнал разрешения конфликтов . 5 (2): 179–196. дои : 10.1177/002200276100500205 .

[155] Аоки, Рюта; Ёмогида, Юкихито; Мацумото, Кендзи (январь 2015 г.). «Нейронные основы оценки социального равенства». Неврологические исследования . 90 : 33–40. дои : 10.1016/j.neures.2014.10.020 . ПМИД 25452125 .

[156] Берг, Джойс; Дикхо, Джон; Маккейб, Кевин (июль 1995 г.). «Доверие, взаимность и социальная история». Игры и экономическое поведение . 10 (1): 122–142. дои : 10.1006/game.1995.1027 .

[157] Джонсон, Ноэль Д.; Мислин, Александра А. (октябрь 2011 г.). «Игры на доверие: метаанализ». Журнал экономической психологии . 32 (5): 865–889. дои : 10.1016/j.joep.2011.05.007 .

[158] «Равновесие Курно (Нэша)» . ОЭСР . 18 апреля 2013 г. Архивировано из оригинала 23 мая 2021 г. . Проверено 20 апреля 2021 г.

[159] Спулбер, Дэниел Ф. (1995). «Конкуренция Бертрана, когда затраты соперников неизвестны». Журнал промышленной экономики . 43 (1): 1–11. дои : 10.2307/2950422 . JSTOR 2950422 .

[160] Насар, Сильвия (1998) Прекрасный разум , Саймон и Шустер. ISBN 0-684-81906-6 .

[161] Сингх, Саймон (14 июня 1998 г.). «Между гением и безумием» . Нью-Йорк Таймс .

[162] Хайнлайн, Роберт А. (1959), Звездный десант

[163] Доктор Стрейнджлав, или Как я научился не волноваться и полюбил бомбу . 29 января 1964 года. 51 минута. ... в том, что весь смысл машины судного дня утерян, если держать это в секрете!

[intpacsun-164] Гузман, Рафер (6 марта 1996 г.). «Звезда в ожидании: верные поклонники, скудные продажи» . Тихоокеанское солнце . Архивировано из оригинала 6 ноября 2013 года . Проверено 25 июля 2018 г. .

[165] «Игра лжеца (манга) - Anime News Network» . www.animenewsnetwork.com . Архивировано из оригинала 25 ноября 2022 года . Проверено 25 ноября 2022 г.

[166] Чаффин, Шон (20 августа 2018 г.). «Покер и теория игр в популярном фильме «Безумно богатые азиаты» » . PokerNews.com. Архивировано из оригинала 5 ноября 2022 года . Проверено 5 ноября 2022 г.

[167] Бин, Трэвис (8 февраля 2019 г.). «Теория игр в «Безумно богатых азиатах»: объяснение разборок в маджонге между Рэйчел и Элеонорой» . Колосс. Архивировано из оригинала 5 ноября 2022 года . Проверено 5 ноября 2022 г.

[168] «Анализ применения сетей в «Игре Молли»: блог курса по сетям для INFO 2040/CS 2850/Econ 2040/SOC 2090» . Архивировано из оригинала 8 апреля 2023 года . Проверено 8 апреля 2023 г.

[1]

[2]

[3]

[4]

[5]

[6]

[7]

[8]

[9]

[10]

[11]

[12]

[13]

[14]

[15]

[16]

[а]

[17]

[18]

[19]

[20]

[21]

[22]

[23]

[24]

[25]

[26]

[27]

[28]

[29]

[30]

[31]

[32]

[33]

[34]

[35]

[36]

[37]

[38]

[39]

[40]

[41]

[42]

[43]

[44]

[45]

[46]

[47]

[48]

[49]

[50]

[51]

[52]

[53]

[54]

[55]

[56]

[57]

[58]

[59]

[60]

[61]

[62]

[63]

[64]

[65]

[66]

[67]

[68]

[69]

[70]

[71]

[72]

[73]

[б]

[75]

[с]

[76]

[77]

[78]

[79]

[80]

[81]

[82]

[83]

[84]

[85]

[86]

[87]

[88]

[89]

[90]

[91]

[92]

[93]

[94]

[95]

[96]

[97]

[98]

v т и Темы теории игр
Definitions	Congestion game Cooperative game Determinacy Escalation of commitment Extensive-form game First-player and second-player win Game complexity Graphical game Hierarchy of beliefs Information set Normal-form game Preference Sequential game Simultaneous game Simultaneous action selection Solved game Succinct game Mechanism design
Equilibrium concepts	Bayes correlated equilibrium Bayesian Nash equilibrium Berge equilibrium Core Correlated equilibrium Coalition-proof Nash equilibrium Epsilon-equilibrium Evolutionarily stable strategy Gibbs equilibrium Mertens-stable equilibrium Markov perfect equilibrium Nash equilibrium Pareto efficiency Perfect Bayesian equilibrium Proper equilibrium Quantal response equilibrium Quasi-perfect equilibrium Risk dominance Satisfaction equilibrium Self-confirming equilibrium Sequential equilibrium Shapley value Strong Nash equilibrium Subgame perfection Trembling hand equilibrium
Strategies	Appeasement Backward induction Bid shading Collusion Cheap talk De-escalation Deterrence Escalation Forward induction Grim trigger Markov strategy Dominant strategies Pure strategy Mixed strategy Strategy-stealing argument Tit for tat
Classes of games	Auction Bargaining problem Global game Intransitive game Mean-field game n-player game Perfect information Large Poisson game Potential game Repeated game Screening game Signaling game Strictly determined game Stochastic game Symmetric game Zero-sum game
Games	Go Chess Infinite chess Checkers All-pay auction Prisoner's dilemma Gift-exchange game Optional prisoner's dilemma Traveler's dilemma Coordination game Chicken Centipede game Lewis signaling game Volunteer's dilemma Dollar auction Battle of the sexes Stag hunt Matching pennies Ultimatum game Electronic mail game Rock paper scissors Pirate game Dictator game Public goods game Blotto game War of attrition El Farol Bar problem Fair division Fair cake-cutting Bertrand competition Cournot competition Stackelberg competition Deadlock Diner's dilemma Guess 2/3 of the average Kuhn poker Nash bargaining game Induction puzzles Trust game Princess and monster game Rendezvous problem
Theorems	Aumann's agreement theorem Folk theorem Minimax theorem Nash's theorem Negamax theorem Purification theorem Revelation principle Sprague–Grundy theorem Zermelo's theorem
Key figures	Albert W. Tucker Amos Tversky Antoine Augustin Cournot Ariel Rubinstein Claude Shannon Daniel Kahneman David K. Levine David M. Kreps Donald B. Gillies Drew Fudenberg Eric Maskin Harold W. Kuhn Herbert Simon Hervé Moulin John Conway Jean Tirole Jean-François Mertens Jennifer Tour Chayes John Harsanyi John Maynard Smith John Nash John von Neumann Kenneth Arrow Kenneth Binmore Leonid Hurwicz Lloyd Shapley Melvin Dresher Merrill M. Flood Olga Bondareva Oskar Morgenstern Paul Milgrom Peyton Young Reinhard Selten Robert Axelrod Robert Aumann Robert B. Wilson Roger Myerson Samuel Bowles Suzanne Scotchmer Thomas Schelling William Vickrey
Miscellaneous	Alpha–beta pruning Bounded rationality Combinatorial game theory Confrontation analysis Coopetition Evolutionary game theory Glossary of game theory List of game theorists List of games in game theory No-win situation Topological game Tragedy of the commons

v т и Основные математики области
History Timeline Future Lists Glossary
Foundations	Category theory Information theory Mathematical logic Philosophy of mathematics Set theory Type theory
Algebra	Abstract Commutative Elementary Group theory Linear Multilinear Universal Homological
Analysis	Calculus Real analysis Complex analysis Hypercomplex analysis Differential equations Functional analysis Harmonic analysis Measure theory
Discrete	Combinatorics Graph theory Order theory
Geometry	Algebraic Analytic Arithmetic Differential Discrete Euclidean Finite
Number theory	Arithmetic Algebraic number theory Analytic number theory Diophantine geometry
Topology	General Algebraic Differential Geometric Homotopy theory
Applied	Engineering mathematics Mathematical biology Mathematical chemistry Mathematical economics Mathematical finance Mathematical physics Mathematical psychology Mathematical sociology Mathematical statistics Probability Statistics Systems science Control theory Game theory Operations research
Computational	Computer science Theory of computation Computational complexity theory Numerical analysis Optimization Computer algebra
Related topics	Mathematicians lists Informal mathematics Films about mathematicians Recreational mathematics Mathematics and art Mathematics education
Mathematics portal Category Commons WikiProject

v т и Микроэкономика
Major topics	Aggregation Budget set Consumer choice Convexity and non-convexity Cost Average Marginal Opportunity Implicit Social Sunk Transaction Cost–benefit analysis Deadweight loss Distribution Economies of scale Economies of scope Elasticity Cross elasticity of demand Income elasticity of demand Price elasticity of demand Price elasticity of supply Equilibrium General Exchange Externality Firms Goods and services Goods Service Household Income–consumption curve Information Indifference curve Intertemporal choice Market Market failure Market structure Competition Monopolistic Perfect Duopoly Monopoly Bilateral Complementary Monopsony Oligopoly Oligopsony Pareto efficiency Preferences Price Price controls Price ceiling Price floor Price discrimination Price signal Price system/Free Pricing Production Profit Public goods Rationing Rent Returns to scale Risk aversion Scarcity Shortage/Excess supply Substitution effect Surplus Social choice Supply and demand Demand/Law of demand Supply/Law of supply Uncertainty Utility Expected Marginal Wage
Subfields	Behavioral Business Computational Development Statistical decision theory Econometrics Engineering economics Civil engineering economics Evolutionary Experimental Game theory Green Industrial organization Institutional Labor Law Managerial Mathematical Microfoundations of macroeconomics Operations research Optimization Welfare
See also	Economics Applied Macroeconomics Political economy
Business portal Category

Базы данных авторитетного контроля
International	FAST
National	Spain France BnF data Germany Israel United States Japan Czech Republic
Other	IdRef 2