Прилив

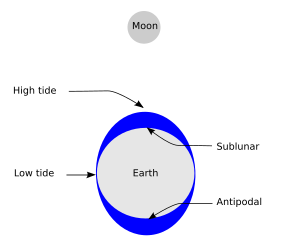
Tide coming in, video stops about 11⁄2 hours before high tide

Приливы — это подъем и понижение уровня моря , вызванные совместным воздействием гравитационных сил , оказываемых Луной (и, в гораздо меньшей степени, Солнцем ), а также вызваны вращением Земли и Луны вокруг друг друга.

Таблицы приливов можно использовать для любого региона, чтобы найти прогнозируемое время и амплитуду (или « диапазон приливов »). На прогнозы влияют многие факторы, включая расположение Солнца и Луны, фазу и амплитуду прилива (характер приливов в глубоком океане), амфидромные системы океанов, а также форму береговой линии и прибрежной зоны. батиметрия (см. Хронометраж ). Однако это всего лишь прогнозы: фактическое время и высота прилива зависят от ветра и атмосферного давления . На многих береговых линиях приливы происходят полусуточно – два почти равных прилива и отлива каждый день. В других местах приливы бывают суточные — по одному приливу и отливу каждый день. «Смешанный прилив» — два прилива разной величины в день — является третьей регулярной категорией. ^[1]^[2]^[a]

Tides vary on timescales ranging from hours to years due to a number of factors, which determine the lunitidal interval. To make accurate records, tide gauges at fixed stations measure water level over time. Gauges ignore variations caused by waves with periods shorter than minutes. These data are compared to the reference (or datum) level usually called mean sea level.^[3]

While tides are usually the largest source of short-term sea-level fluctuations, sea levels are also subject to change from thermal expansion, wind, and barometric pressure changes, resulting in storm surges, especially in shallow seas and near coasts.

Tidal phenomena are not limited to the oceans, but can occur in other systems whenever a gravitational field that varies in time and space is present. For example, the shape of the solid part of the Earth is affected slightly by Earth tide, though this is not as easily seen as the water tidal movements.

Characteristics

Four stages in the tidal cycle are named:

The water stops falling, reaching a local minimum called low tide.
Sea level rises over several hours, covering the intertidal zone; flood tide.
The water stops rising, reaching a local maximum called high tide.
Sea level falls over several hours, revealing the intertidal zone; ebb tide.

Oscillating currents produced by tides are known as tidal streams or tidal currents. The moment that the tidal current ceases is called slack water or slack tide. The tide then reverses direction and is said to be turning. Slack water usually occurs near high water and low water, but there are locations where the moments of slack tide differ significantly from those of high and low water.^[4]

Tides are commonly semi-diurnal (two high waters and two low waters each day), or diurnal (one tidal cycle per day). The two high waters on a given day are typically not the same height (the daily inequality); these are the higher high water and the lower high water in tide tables. Similarly, the two low waters each day are the higher low water and the lower low water. The daily inequality is not consistent and is generally small when the Moon is over the Equator.^[b]

Reference levels

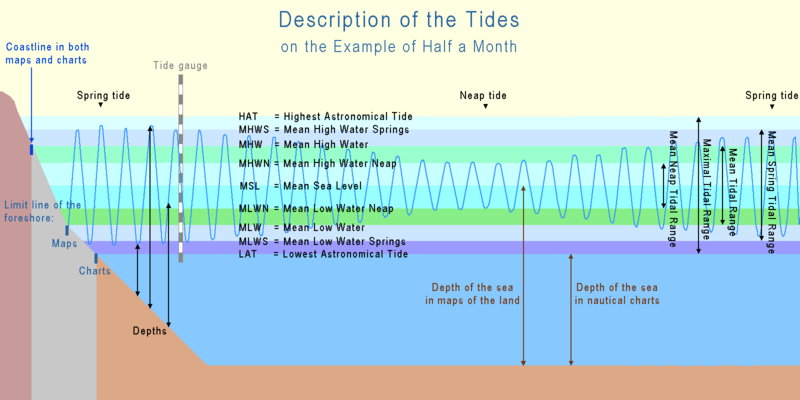
The following reference tide levels can be defined, from the highest level to the lowest:

Highest astronomical tide (HAT) – The highest tide which can be predicted to occur. Note that meteorological conditions may add extra height to the HAT.
Mean high water springs (MHWS) – The average of the two high tides on the days of spring tides.
Mean high water neaps (MHWN) – The average of the two high tides on the days of neap tides.
Mean sea level (MSL) – This is the average sea level. The MSL is constant for any location over a long period.
Mean low water neaps (MLWN) – The average of the two low tides on the days of neap tides.
Mean low water springs (MLWS) – The average of the two low tides on the days of spring tides.
Lowest astronomical tide (LAT) – The lowest tide which can be predicted to occur.^[6]

Tidal constituents

Tidal constituents are the net result of multiple influences impacting tidal changes over certain periods of time. Primary constituents include the Earth's rotation, the position of the Moon and Sun relative to the Earth, the Moon's altitude (elevation) above the Earth's Equator, and bathymetry. Variations with periods of less than half a day are called harmonic constituents. Conversely, cycles of days, months, or years are referred to as long period constituents.

Tidal forces affect the entire earth, but the movement of solid Earth occurs by mere centimeters. In contrast, the atmosphere is much more fluid and compressible so its surface moves by kilometers, in the sense of the contour level of a particular low pressure in the outer atmosphere.

Principal lunar semi-diurnal constituent

Global surface elevation of M2 ocean tide (NASA)^[7]

In most locations, the largest constituent is the principal lunar semi-diurnal, also known as the M2 tidal constituent or M₂ tidal constituent. Its period is about 12 hours and 25.2 minutes, exactly half a tidal lunar day, which is the average time separating one lunar zenith from the next, and thus is the time required for the Earth to rotate once relative to the Moon. Simple tide clocks track this constituent. The lunar day is longer than the Earth day because the Moon orbits in the same direction the Earth spins. This is analogous to the minute hand on a watch crossing the hour hand at 12:00 and then again at about 1:05+1⁄2 (not at 1:00).

The Moon orbits the Earth in the same direction as the Earth rotates on its axis, so it takes slightly more than a day—about 24 hours and 50 minutes—for the Moon to return to the same location in the sky. During this time, it has passed overhead (culmination) once and underfoot once (at an hour angle of 00:00 and 12:00 respectively), so in many places the period of strongest tidal forcing is the above-mentioned, about 12 hours and 25 minutes. The moment of highest tide is not necessarily when the Moon is nearest to zenith or nadir, but the period of the forcing still determines the time between high tides.

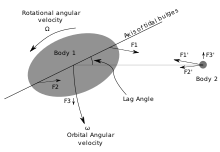
Because the gravitational field created by the Moon weakens with distance from the Moon, it exerts a slightly stronger than average force on the side of the Earth facing the Moon, and a slightly weaker force on the opposite side. The Moon thus tends to "stretch" the Earth slightly along the line connecting the two bodies. The solid Earth deforms a bit, but ocean water, being fluid, is free to move much more in response to the tidal force, particularly horizontally (see equilibrium tide).

As the Earth rotates, the magnitude and direction of the tidal force at any particular point on the Earth's surface change constantly; although the ocean never reaches equilibrium—there is never time for the fluid to "catch up" to the state it would eventually reach if the tidal force were constant—the changing tidal force nonetheless causes rhythmic changes in sea surface height.

When there are two high tides each day with different heights (and two low tides also of different heights), the pattern is called a mixed semi-diurnal tide.^[8]

Range variation: springs and neaps

The semi-diurnal range (the difference in height between high and low waters over about half a day) varies in a two-week cycle. Approximately twice a month, around new moon and full moon when the Sun, Moon, and Earth form a line (a configuration known as a syzygy^[9]), the tidal force due to the Sun reinforces that due to the Moon. The tide's range is then at its maximum; this is called the spring tide. It is not named after the season, but, like that word, derives from the meaning "jump, burst forth, rise", as in a natural spring. Spring tides are sometimes referred to as syzygy tides.^[10]

When the Moon is at first quarter or third quarter, the Sun and Moon are separated by 90° when viewed from the Earth, and the solar tidal force partially cancels the Moon's tidal force. At these points in the lunar cycle, the tide's range is at its minimum; this is called the neap tide, or neaps. "Neap" is an Anglo-Saxon word meaning "without the power", as in forðganges nip (forth-going without-the-power).^[11]Neap tides are sometimes referred to as quadrature tides.^[10]

Spring tides result in high waters that are higher than average, low waters that are lower than average, "slack water" time that is shorter than average, and stronger tidal currents than average. Neaps result in less extreme tidal conditions. There is about a seven-day interval between springs and neaps.

Spring tide: Sun and Moon on the same side (0°)
Neap tide: Sun and Moon at 90°
Spring tide: Sun and Moon at opposite sides (180°)
Neap tide: Sun and Moon at 270°
Spring tide: Sun and Moon at the same side (cycle restarts)

Lunar distance

The changing distance separating the Moon and Earth also affects tide heights. When the Moon is closest, at perigee, the range increases, and when it is at apogee, the range shrinks. Six or eight times a year perigee coincides with either a new or full moon causing perigean spring tides with the largest tidal range. The difference between the height of a tide at perigean spring tide and the spring tide when the moon is at apogee depends on location but can be large as a foot higher.^[12]

Other constituents

These include solar gravitational effects, the obliquity (tilt) of the Earth's Equator and rotational axis, the inclination of the plane of the lunar orbit and the elliptical shape of the Earth's orbit of the Sun.

A compound tide (or overtide) results from the shallow-water interaction of its two parent waves.^[13]

Phase and amplitude

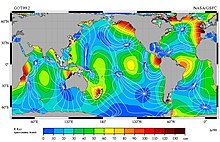
Because the M₂ tidal constituent dominates in most locations, the stage or phase of a tide, denoted by the time in hours after high water, is a useful concept. Tidal stage is also measured in degrees, with 360° per tidal cycle. Lines of constant tidal phase are called cotidal lines, which are analogous to contour lines of constant altitude on topographical maps, and when plotted form a cotidal map or cotidal chart.^[16] High water is reached simultaneously along the cotidal lines extending from the coast out into the ocean, and cotidal lines (and hence tidal phases) advance along the coast. Semi-diurnal and long phase constituents are measured from high water, diurnal from maximum flood tide. This and the discussion that follows is precisely true only for a single tidal constituent.

For an ocean in the shape of a circular basin enclosed by a coastline, the cotidal lines point radially inward and must eventually meet at a common point, the amphidromic point. The amphidromic point is at once cotidal with high and low waters, which is satisfied by zero tidal motion. (The rare exception occurs when the tide encircles an island, as it does around New Zealand, Iceland and Madagascar.) Tidal motion generally lessens moving away from continental coasts, so that crossing the cotidal lines are contours of constant amplitude (half the distance between high and low water) which decrease to zero at the amphidromic point. For a semi-diurnal tide the amphidromic point can be thought of roughly like the center of a clock face, with the hour hand pointing in the direction of the high water cotidal line, which is directly opposite the low water cotidal line. High water rotates about the amphidromic point once every 12 hours in the direction of rising cotidal lines, and away from ebbing cotidal lines. This rotation, caused by the Coriolis effect, is generally clockwise in the southern hemisphere and counterclockwise in the northern hemisphere. The difference of cotidal phase from the phase of a reference tide is the epoch. The reference tide is the hypothetical constituent "equilibrium tide" on a landless Earth measured at 0° longitude, the Greenwich meridian.^[17]

In the North Atlantic, because the cotidal lines circulate counterclockwise around the amphidromic point, the high tide passes New York Harbor approximately an hour ahead of Norfolk Harbor. South of Cape Hatteras the tidal forces are more complex, and cannot be predicted reliably based on the North Atlantic cotidal lines.

History

History of tidal theory

Investigation into tidal physics was important in the early development of celestial mechanics, with the existence of two daily tides being explained by the Moon's gravity. Later the daily tides were explained more precisely by the interaction of the Moon's and the Sun's gravity.

Seleucus of Seleucia theorized around 150 BC that tides were caused by the Moon. The influence of the Moon on bodies of water was also mentioned in Ptolemy's Tetrabiblos.^[c]

In De temporum ratione (The Reckoning of Time) of 725 Bede linked semidurnal tides and the phenomenon of varying tidal heights to the Moon and its phases. Bede starts by noting that the tides rise and fall 4/5 of an hour later each day, just as the Moon rises and sets 4/5 of an hour later.^[19] He goes on to emphasise that in two lunar months (59 days) the Moon circles the Earth 57 times and there are 114 tides.^[20] Bede then observes that the height of tides varies over the month. Increasing tides are called malinae and decreasing tides ledones and that the month is divided into four parts of seven or eight days with alternating malinae and ledones.^[21] In the same passage he also notes the effect of winds to hold back tides.^[21] Bede also records that the time of tides varies from place to place. To the north of Bede's location (Monkwearmouth) the tides are earlier, to the south later.^[22] He explains that the tide "deserts these shores in order to be able all the more to be able to flood other [shores] when it arrives there" noting that "the Moon which signals the rise of tide here, signals its retreat in other regions far from this quarter of the heavens".^[22]

Later medieval understanding of the tides was primarily based on works of Muslim astronomers, which became available through Latin translation starting from the 12th century.^[23] Abu Ma'shar al-Balkhi (d. circa 886), in his Introductorium in astronomiam, taught that ebb and flood tides were caused by the Moon.^[23] Abu Ma'shar discussed the effects of wind and Moon's phases relative to the Sun on the tides.^[23] In the 12th century, al-Bitruji (d. circa 1204) contributed the notion that the tides were caused by the general circulation of the heavens.^[23]

Simon Stevin, in his 1608 De spiegheling der Ebbenvloet (The theory of ebb and flood), dismissed a large number of misconceptions that still existed about ebb and flood. Stevin pleaded for the idea that the attraction of the Moon was responsible for the tides and spoke in clear terms about ebb, flood, spring tide and neap tide, stressing that further research needed to be made.^[24]^[25]

In 1609 Johannes Kepler also correctly suggested that the gravitation of the Moon caused the tides,^[d] which he based upon ancient observations and correlations.

Galileo Galilei in his 1632 Dialogue Concerning the Two Chief World Systems, whose working title was Dialogue on the Tides, gave an explanation of the tides. The resulting theory, however, was incorrect as he attributed the tides to the sloshing of water caused by the Earth's movement around the Sun. He hoped to provide mechanical proof of the Earth's movement. The value of his tidal theory is disputed. Galileo rejected Kepler's explanation of the tides.

Isaac Newton (1642–1727) was the first person to explain tides as the product of the gravitational attraction of astronomical masses. His explanation of the tides (and many other phenomena) was published in the Principia (1687)^[27]^[28] and used his theory of universal gravitation to explain the lunar and solar attractions as the origin of the tide-generating forces.^[e]Newton and others before Pierre-Simon Laplace worked the problem from the perspective of a static system (equilibrium theory), that provided an approximation that described the tides that would occur in a non-inertial ocean evenly covering the whole Earth.^[27] The tide-generating force (or its corresponding potential) is still relevant to tidal theory, but as an intermediate quantity (forcing function) rather than as a final result; theory must also consider the Earth's accumulated dynamic tidal response to the applied forces, which response is influenced by ocean depth, the Earth's rotation, and other factors.^[29]

In 1740, the Académie Royale des Sciences in Paris offered a prize for the best theoretical essay on tides. Daniel Bernoulli, Leonhard Euler, Colin Maclaurin and Antoine Cavalleri shared the prize.^[30]

Maclaurin used Newton's theory to show that a smooth sphere covered by a sufficiently deep ocean under the tidal force of a single deforming body is a prolate spheroid (essentially a three-dimensional oval) with major axis directed toward the deforming body. Maclaurin was the first to write about the Earth's rotational effects on motion. Euler realized that the tidal force's horizontal component (more than the vertical) drives the tide. In 1744 Jean le Rond d'Alembert studied tidal equations for the atmosphere which did not include rotation.

In 1770 James Cook's barque HMS Endeavour grounded on the Great Barrier Reef. Attempts were made to refloat her on the following tide which failed, but the tide after that lifted her clear with ease. Whilst she was being repaired in the mouth of the Endeavour River Cook observed the tides over a period of seven weeks. At neap tides both tides in a day were similar, but at springs the tides rose 7 feet (2.1 m) in the morning but 9 feet (2.7 m) in the evening.^[31]

Pierre-Simon Laplace formulated a system of partial differential equations relating the ocean's horizontal flow to its surface height, the first major dynamic theory for water tides. The Laplace tidal equations are still in use today. William Thomson, 1st Baron Kelvin, rewrote Laplace's equations in terms of vorticity which allowed for solutions describing tidally driven coastally trapped waves, known as Kelvin waves.^[32]^[33]^[34]

Others including Kelvin and Henri Poincaré further developed Laplace's theory. Based on these developments and the lunar theory of E W Brown describing the motions of the Moon, Arthur Thomas Doodson developed and published in 1921^[35] the first modern development of the tide-generating potential in harmonic form: Doodson distinguished 388 tidal frequencies.^[36] Some of his methods remain in use.^[37]

History of tidal observation

From ancient times, tidal observation and discussion has increased in sophistication, first marking the daily recurrence, then tides' relationship to the Sun and moon. Pytheas travelled to the British Isles about 325 BC and seems to be the first to have related spring tides to the phase of the moon.

In the 2nd century BC, the Hellenistic astronomer Seleucus of Seleucia correctly described the phenomenon of tides in order to support his heliocentric theory.^[38] He correctly theorized that tides were caused by the moon, although he believed that the interaction was mediated by the pneuma. He noted that tides varied in time and strength in different parts of the world. According to Strabo (1.1.9), Seleucus was the first to link tides to the lunar attraction, and that the height of the tides depends on the moon's position relative to the Sun.^[39]

The Naturalis Historia of Pliny the Elder collates many tidal observations, e.g., the spring tides are a few days after (or before) new and full moon and are highest around the equinoxes, though Pliny noted many relationships now regarded as fanciful. In his Geography, Strabo described tides in the Persian Gulf having their greatest range when the moon was furthest from the plane of the Equator. All this despite the relatively small amplitude of Mediterranean basin tides. (The strong currents through the Euripus Strait and the Strait of Messina puzzled Aristotle.) Philostratus discussed tides in Book Five of The Life of Apollonius of Tyana. Philostratus mentions the moon, but attributes tides to "spirits". In Europe around 730 AD, the Venerable Bede described how the rising tide on one coast of the British Isles coincided with the fall on the other and described the time progression of high water along the Northumbrian coast.

The first tide table in China was recorded in 1056 AD primarily for visitors wishing to see the famous tidal bore in the Qiantang River. The first known British tide table is thought to be that of John Wallingford, who died Abbot of St. Albans in 1213, based on high water occurring 48 minutes later each day, and three hours earlier at the Thames mouth than upriver at London.^[40]

In 1614 Claude d'Abbeville published the work "Histoire de la mission de pères capucins en l'Isle de Maragnan et terres circonvoisines", where he exposed that the Tupinambá people already had an understanding of the relation between the Moon and the tides before Europe.^[41]

William Thomson (Lord Kelvin) led the first systematic harmonic analysis of tidal records starting in 1867. The main result was the building of a tide-predicting machine using a system of pulleys to add together six harmonic time functions. It was "programmed" by resetting gears and chains to adjust phasing and amplitudes. Similar machines were used until the 1960s.^[42]

The first known sea-level record of an entire spring–neap cycle was made in 1831 on the Navy Dock in the Thames Estuary. Many large ports had automatic tide gauge stations by 1850.

John Lubbock was one of the first to map co-tidal lines, for Great Britain, Ireland and adjacent coasts, in 1840.^[43] William Whewell expanded this work ending with a nearly global chart in 1836.^[44] In order to make these maps consistent, he hypothesized the existence of a region with no tidal rise or fall where co-tidal lines meet in the mid-ocean. The existence of such an amphidromic point, as they are now known, was confirmed in 1840 by Captain William Hewett, RN, from careful soundings in the North Sea.^[45]^[46]^[32]

Much later, in the late 20th century, geologists noticed tidal rhythmites, which document the occurrence of ancient tides in the geological record, notably in the Carboniferous.^[47]^[48]

Physics

Forces

The tidal force produced by a massive object (Moon, hereafter) on a small particle located on or in an extensive body (Earth, hereafter) is the vector difference between the gravitational force exerted by the Moon on the particle, and the gravitational force that would be exerted on the particle if it were located at the Earth's center of mass.

Whereas the gravitational force subjected by a celestial body on Earth varies inversely as the square of its distance to the Earth, the maximal tidal force varies inversely as, approximately, the cube of this distance.^[49] If the tidal force caused by each body were instead equal to its full gravitational force (which is not the case due to the free fall of the whole Earth, not only the oceans, towards these bodies) a different pattern of tidal forces would be observed, e.g. with a much stronger influence from the Sun than from the Moon: The solar gravitational force on the Earth is on average 179 times stronger than the lunar, but because the Sun is on average 389 times farther from the Earth, its field gradient is weaker. The overall proportionality is

{\text{tidal force}}\propto {\frac {M}{d^{3}}}\propto \rho \left({\frac {r}{d}}\right)^{3},

where $M$ is the mass of the heavenly body, $d$ is its distance, $ρ$ is its average density, and $r$ is its radius. The ratio $r / d$ is related to the angle subtended by the object in the sky. Since the Sun and the Moon have practically the same diameter in the sky, the tidal force of the Sun is less than that of the Moon because its average density is much less, and it is only 46% as large as the lunar,^[f] thus during a spring tide, the Moon contributes 69% while the Sun contributes 31%. More precisely, the lunar tidal acceleration (along the Moon–Earth axis, at the Earth's surface) is about 1.1×10⁻⁷ g, while the solar tidal acceleration (along the Sun–Earth axis, at the Earth's surface) is about 0.52×10⁻⁷ g, where g is the gravitational acceleration at the Earth's surface.^[g] The effects of the other planets vary as their distances from Earth vary. When Venus is closest to Earth, its effect is 0.000113 times the solar effect.^[50] At other times, Jupiter or Mars may have the most effect.

The ocean's surface is approximated by a surface referred to as the geoid, which takes into consideration the gravitational force exerted by the earth as well as centrifugal force due to rotation. Now consider the effect of massive external bodies such as the Moon and Sun. These bodies have strong gravitational fields that diminish with distance and cause the ocean's surface to deviate from the geoid. They establish a new equilibrium ocean surface which bulges toward the moon on one side and away from the moon on the other side. The earth's rotation relative to this shape causes the daily tidal cycle. The ocean surface tends toward this equilibrium shape, which is constantly changing, and never quite attains it. When the ocean surface is not aligned with it, it's as though the surface is sloping, and water accelerates in the down-slope direction.

Equilibrium

The equilibrium tide is the idealized tide assuming a landless Earth.^[51]It would produce a tidal bulge in the ocean, elongated towards the attracting body (Moon or Sun).It is not caused by the vertical pull nearest or farthest from the body, which is very weak; rather, it is caused by the tangential or tractive tidal force, which is strongest at about 45 degrees from the body, resulting in a horizontal tidal current.^[h]^[i]^[j]^[55]

Laplace's tidal equations

Ocean depths are much smaller than their horizontal extent. Thus, the response to tidal forcing can be modelled using the Laplace tidal equations which incorporate the following features:

The vertical (or radial) velocity is negligible, and there is no vertical shear—this is a sheet flow.
The forcing is only horizontal (tangential).
The Coriolis effect appears as an inertial force (fictitious) acting laterally to the direction of flow and proportional to velocity.
The surface height's rate of change is proportional to the negative divergence of velocity multiplied by the depth. As the horizontal velocity stretches or compresses the ocean as a sheet, the volume thins or thickens, respectively.

The boundary conditions dictate no flow across the coastline and free slip at the bottom.

The Coriolis effect (inertial force) steers flows moving towards the Equator to the west and flows moving away from the Equator toward the east, allowing coastally trapped waves. Finally, a dissipation term can be added which is an analog to viscosity.

Amplitude and cycle time

The theoretical amplitude of oceanic tides caused by the Moon is about 54 centimetres (21 in) at the highest point, which corresponds to the amplitude that would be reached if the ocean possessed a uniform depth, there were no landmasses, and the Earth were rotating in step with the Moon's orbit. The Sun similarly causes tides, of which the theoretical amplitude is about 25 centimetres (9.8 in) (46% of that of the Moon) with a cycle time of 12 hours. At spring tide the two effects add to each other to a theoretical level of 79 centimetres (31 in), while at neap tide the theoretical level is reduced to 29 centimetres (11 in). Since the orbits of the Earth about the Sun, and the Moon about the Earth, are elliptical, tidal amplitudes change somewhat as a result of the varying Earth–Sun and Earth–Moon distances. This causes a variation in the tidal force and theoretical amplitude of about ±18% for the Moon and ±5% for the Sun. If both the Sun and Moon were at their closest positions and aligned at new moon, the theoretical amplitude would reach 93 centimetres (37 in).

Real amplitudes differ considerably, not only because of depth variations and continental obstacles, but also because wave propagation across the ocean has a natural period of the same order of magnitude as the rotation period: if there were no land masses, it would take about 30 hours for a long wavelength surface wave to propagate along the Equator halfway around the Earth (by comparison, the Earth's lithosphere has a natural period of about 57 minutes). Earth tides, which raise and lower the bottom of the ocean, and the tide's own gravitational self attraction are both significant and further complicate the ocean's response to tidal forces.

Dissipation

Earth's tidal oscillations introduce dissipation at an average rate of about 3.75 terawatts.^[56] About 98% of this dissipation is by marine tidal movement.^[57] Dissipation arises as basin-scale tidal flows drive smaller-scale flows which experience turbulent dissipation. This tidal drag creates torque on the moon that gradually transfers angular momentum to its orbit, and a gradual increase in Earth–moon separation. The equal and opposite torque on the Earth correspondingly decreases its rotational velocity. Thus, over geologic time, the moon recedes from the Earth, at about 3.8 centimetres (1.5 in)/year, lengthening the terrestrial day.^[k]

Day length has increased by about 2 hours in the last 600 million years. Assuming (as a crude approximation) that the deceleration rate has been constant, this would imply that 70 million years ago, day length was on the order of 1% shorter with about 4 more days per year.

Bathymetry

The shape of the shoreline and the ocean floor changes the way that tides propagate, so there is no simple, general rule that predicts the time of high water from the Moon's position in the sky. Coastal characteristics such as underwater bathymetry and coastline shape mean that individual location characteristics affect tide forecasting; actual high water time and height may differ from model predictions due to the coastal morphology's effects on tidal flow. However, for a given location the relationship between lunar altitude and the time of high or low tide (the lunitidal interval) is relatively constant and predictable, as is the time of high or low tide relative to other points on the same coast. For example, the high tide at Norfolk, Virginia, U.S., predictably occurs approximately two and a half hours before the Moon passes directly overhead.

Land masses and ocean basins act as barriers against water moving freely around the globe, and their varied shapes and sizes affect the size of tidal frequencies. As a result, tidal patterns vary. For example, in the U.S., the East coast has predominantly semi-diurnal tides, as do Europe's Atlantic coasts, while the West coast predominantly has mixed tides.^[59]^[60]^[61] Human changes to the landscape can also significantly alter local tides.^[62]

Observation and prediction

Тайминг

Приливные силы, вызванные Луной и Солнцем, создают очень длинные волны, которые распространяются по всему океану по путям, показанным на картах приливов . Время, когда гребень волны достигает порта, дает время паводка в порту. Время, необходимое волне для путешествия по океану, также означает, что существует задержка между фазами Луны и их влиянием на прилив. весны и приливы в Северном море Например, прилива отстают на два дня от новолуния/полнолуния и первой/третьей четверти луны. Это называется возрастом . ^[63]^[64]

океана Батиметрия сильно влияет на точное время и высоту прилива в конкретной точке побережья . Есть несколько крайних случаев; Часто утверждается, что в заливе Фанди на восточном побережье Канады наблюдаются самые высокие в мире приливы из-за его формы, батиметрии и удаленности от края континентального шельфа. ^[65] Измерения, проведенные в ноябре 1998 года на мысе Бернткоат-Хед в заливе Фанди, зафиксировали максимальную дальность 16,3 метра (53 фута) и самый высокий прогнозируемый максимум 17 метров (56 футов). ^[66]^[67] Аналогичные измерения, проведенные в марте 2002 года в бассейне Лиф в заливе Унгава на севере Квебека , дали аналогичные значения (с учетом ошибок измерений), максимальную дальность 16,2 метра (53 фута) и самый высокий прогнозируемый экстремум 16,8 метра (55 футов). ^[66]^[67] Заливы Унгава и залив Фанди находятся на одинаковом расстоянии от края континентального шельфа, но залив Унгава свободен от пакового льда только около четырех месяцев в году, а залив Фанди редко замерзает.

В Саутгемптоне в Соединенном Королевстве наблюдается двойной паводок, вызванный взаимодействием M ₂ и M ₄ приливных составляющих (мелководные приливы главной луны). ^[68] По той же причине в Портленде наблюдается двойной межень. Прилив М ₄ наблюдается по всему южному побережью Соединенного Королевства, но его влияние наиболее заметно между островом Уайт и Портлендом , поскольку прилив М ₂ в этом регионе самый низкий.

Поскольку режимы колебаний Средиземного и Балтийского морей не совпадают с каким-либо значительным периодом астрономических воздействий, самые крупные приливы близки к их узким соединениям с Атлантическим океаном. По той же причине происходят чрезвычайно малые приливы в Мексиканском заливе и Японском море . В других местах, например, вдоль южного побережья Австралии , отливы могут быть связаны с наличием поблизости амфидрома .

Анализ

Исаака Ньютона Теория гравитации впервые позволила объяснить, почему обычно бывает два прилива в день, а не один, и дала надежду на детальное понимание приливных сил и поведения. Хотя может показаться, что приливы можно предсказать с помощью достаточно детального знания мгновенных астрономических воздействий, фактический прилив в данном месте определяется астрономическими силами, накопленными водоемом за многие дни. Кроме того, для получения точных результатов потребуются детальные знания формы всех океанских бассейнов — их батиметрии и формы береговой линии.

Текущая процедура анализа приливов следует методу гармонического анализа, введенному в 1860-х годах Уильямом Томсоном . Он основан на том принципе, что астрономические теории движения Солнца и Луны определяют большое количество составляющих частот, и на каждой частоте существует составляющая силы, стремящаяся вызвать приливное движение, но в каждом интересующем месте на планете На Земле приливы реагируют на каждую частоту с амплитудой и фазой, характерными для этой местности. Поэтому в каждом достопримечательном месте высота прилива измеряется в течение достаточно длительного периода времени (обычно более года в случае нового порта, который ранее не изучался), чтобы можно было различить реакцию на каждой значительной частоте возникновения приливов. путем анализа и извлечь приливные константы для достаточного количества самых сильных известных компонентов астрономических приливных сил, чтобы обеспечить практическое предсказание приливов. Ожидается, что высота прилива будет соответствовать приливной силе с постоянной амплитудой и задержкой фазы для каждого компонента. Поскольку астрономические частоты и фазы могут быть точно рассчитаны, высоту прилива в другое время можно будет предсказать, как только будет найдена реакция на гармонические компоненты астрономических сил, генерирующих приливы.

Основные закономерности приливов:

вариант два раза в день
разница между первым и вторым приливом дня
цикл весна-сборка
годовое изменение

Высший астрономический прилив — это перигейский весенний прилив, когда Солнце и Луна находятся ближе всего к Земле.

Когда мы сталкиваемся с периодически меняющейся функцией, стандартным подходом является использование ряда Фурье — формы анализа, в которой набора используются синусоидальные функции в качестве базисного , имеющие частоты, равные нулю, одному, двум, трем и т. д. раз превышающим частоту конкретной функции. фундаментальный цикл. Эти кратные частоты называются гармониками основной частоты, а сам процесс называется гармоническим анализом . Если базовый набор синусоидальных функций соответствует моделируемому поведению, необходимо добавить относительно немного гармонических членов. Орбитальные траектории почти круговые, поэтому синусоидальные изменения подходят для приливов и отливов.

Для анализа высоты прилива на практике подход с использованием рядов Фурье должен быть более сложным, чем использование одной частоты и ее гармоник. Приливные модели разлагаются на множество синусоид, имеющих множество основных частот, соответствующих (как и в теории Луны ) множеству различных комбинаций движений Земли, Луны и углов, определяющих форму и расположение их орбит.

Таким образом, для приливов гармонический анализ не ограничивается гармониками одной частоты. ^[л] Другими словами, гармонии кратны многим фундаментальным частотам, а не только основной частоте более простого подхода с использованием рядов Фурье. Их представление в виде ряда Фурье, имеющего только одну фундаментальную частоту и ее (целые) кратные, потребовало бы множества терминов и было бы строго ограничено во временном диапазоне, для которого оно было бы справедливо.

Изучение высоты прилива методом гармонического анализа было начато Лапласом, Уильямом Томсоном (лордом Кельвином) и Джорджем Дарвином . AT Doodson расширили свою работу, введя обозначение числа Дудсона для организации сотен результирующих членов. С тех пор этот подход стал международным стандартом, и осложнения возникают следующим образом: сила, вызывающая прилив, условно определяется суммой нескольких слагаемых. Каждый термин имеет вид

A_{o}\cos(\omega t+p),

где

A o

– амплитуда,

ω

— угловая частота, обычно выражаемая в градусах в час, соответствующая

t,

измеряемому в часах,

p

— сдвиг фазы относительно астрономического состояния в момент времени t = 0.

Есть один термин для Луны и второй термин для Солнца. Фаза $p$ первой гармоники лунного термина называется лунным интервалом или интервалом половодья.

Следующее уточнение заключается в учете гармонических членов из-за эллиптической формы орбит. Для этого значение амплитуды принимают не постоянным, а изменяющимся во времени около средней амплитуды $А о$ . Для этого замените $A o$ в приведенном выше уравнении на $A (t)$ , где $A$ — еще одна синусоида, подобная циклам и эпициклам теории Птолемея . Это дает

A(t)=A_{o}{\bigl (}1+A_{a}\cos(\omega _{a}t+p_{a}){\bigr )},

то есть среднее значение $A o$ с синусоидальным изменением вокруг него величины $A a$ с частотой $ω a$ и фазой $p a$ . Подстановка этого значения на $A o$ в исходном уравнении дает произведение двух косинусных множителей:

A_{o}{\bigl (}1+A_{a}\cos(\omega _{a}t+p_{a}){\bigr )}\cos(\omega t+p).

Учитывая, что для любых $x$ и $y$

\cos x\cos y={\tfrac {1}{2}}\cos(x+y)+{\tfrac {1}{2}}\cos(x-y),

ясно, что составной член, включающий в себя произведение двух косинусных членов, каждый из которых имеет свою собственную частоту, аналогичен трем простым косинусным членам, которые должны быть добавлены на исходной частоте, а также на частотах, которые представляют собой сумму и разность двух частот. срока действия продукта. (Три, а не два слагаемых, поскольку все выражение $(1+\cos x)\cos y$ .) Учтите далее, что приливная сила в каком-либо месте зависит также от того, находится ли Луна (или Солнце) выше или ниже плоскости экватора, и что эти атрибуты имеют свои периоды, также несоизмеримые с днем и месяцем, и ясно, что получается множество комбинаций. При тщательном выборе основных астрономических частот число Дудсона аннотирует конкретные дополнения и различия, образуя частоту каждого простого косинусного члена.

Помните, что астрономические приливы не включают погодные эффекты. Кроме того, изменения местных условий (движение песчаных отмелей, дноуглубительные работы в устьях гаваней и т. д.) по сравнению с теми, которые преобладали во время измерения, влияют на фактическое время и величину прилива. Организации, указывающие «самый высокий астрономический прилив» для какого-либо места, могут преувеличивать эту цифру как фактор безопасности в отношении аналитических неопределенностей, расстояния от ближайшей точки измерения, изменений с момента последнего наблюдения, проседания грунта и т. д., чтобы избежать ответственности в случае инженерных работ. быть перегруженным. Особая осторожность необходима при оценке размера «погодного всплеска» путем вычитания астрономического прилива из наблюдаемого прилива.

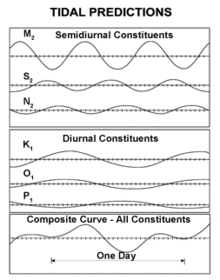
Фурье Тщательный анализ данных за девятнадцатилетний период ( Эпоха национальных приливов в США) использует частоты, называемые составляющими приливных гармоник . Девятнадцать лет предпочтительнее, потому что относительные положения Земли, Луны и Солнца повторяются почти точно в 19-летнем цикле Метона , который достаточно длинный, чтобы включить 18,613-летнюю лунную узловую приливную составляющую . Этот анализ можно провести, используя только знание периода воздействия , но без детального понимания математического вывода, а это означает, что полезные таблицы приливов и отливов строились на протяжении веков. ^[69] Полученные амплитуды и фазы затем можно использовать для прогнозирования ожидаемых приливов. Обычно в них преобладают составляющие около 12 часов ( полусуточные составляющие), но есть основные составляющие около 24 часов ( суточные и ). Долгосрочные составляющие — это 14-дневные или двухнедельные , ежемесячные и полугодовые. На береговой линии преобладали полусуточные приливы, но в некоторых районах, таких как Южно-Китайское море и Мексиканский залив, они преимущественно дневные. В полусуточных областях основные составляющие периодов M ₂ (лунный) и S ₂ (солнечный) различаются незначительно, так что относительные фазы и, следовательно, амплитуда объединенного прилива изменяются каждые две недели (период 14 дней). ^[70]

На приведенном выше графике M ₂ каждая котидальная линия отличается от соседних на один час, а более толстые линии показывают приливы в фазе с равновесием в Гринвиче. линии вращаются вокруг амфидромных точек В северном полушарии против часовой стрелки, так что от полуострова Нижняя Калифорния до Аляски и от Франции до Ирландии прилив М ₂ распространяется на север. В южном полушарии это направление по часовой стрелке. С другой стороны, прилив М ₂ распространяется вокруг Новой Зеландии против часовой стрелки, но это связано с тем, что острова действуют как плотина и позволяют приливам иметь разную высоту на противоположных сторонах островов. (Как и предсказывает теория, приливы распространяются на север на восточной стороне и на юг на западном побережье.)

Исключением является пролив Кука , где приливные течения периодически соединяют высокий уровень воды с низким уровнем воды. Это связано с тем, что котидальные линии на 180 ° вокруг амфидромов находятся в противоположной фазе, например, половодье напротив маловодья на каждом конце пролива Кука. Каждая приливная составляющая имеет различный набор амплитуд, фаз и амфидромных точек, поэтому шаблоны M ₂ нельзя использовать для других компонентов прилива.

Пример расчета

График с одной линией, поднимающейся и опускающейся между 4 пиками около 3 и четырьмя впадинами около −3. — Приливы в Бриджпорте, штат Коннектикут , США, в течение 50 часов.

График с одной линией, показывающий приливные пики и спады, постепенно меняющиеся между более высокими и более низкими максимумами в течение 14-дневного периода. — Приливы в Бриджпорте, штат Коннектикут, США, за 30-дневный период.

График, показывающий одну линию, показывающую только минимальные годовые колебания прилива. — Приливы в Бриджпорте, штат Коннектикут, США, за 400-дневный период.

График, показывающий 6 линий, по две линии для каждого из трех городов. В Нельсоне бывает два весенних прилива в месяц, а в Нейпире и Веллингтоне — по одному. — Приливные режимы в проливе Кука. В южной части (Нельсон) бывает два весенних прилива в месяц, тогда как в северной части (Веллингтон и Нейпир) только один.

Поскольку Луна движется по своей орбите вокруг Земли и в том же смысле, что и вращение Земли, точка на Земле должна вращаться немного дальше, чтобы догнать ее, чтобы время между полусуточными приливами составляло не двенадцать, а 12,4206 часов — чуть больше двадцати пяти минут. Эти две вершины не равны. Два прилива в день чередуются с максимальной высотой: более низкий (чуть менее трех футов), более высокий (чуть более трех футов) и снова более низкий. То же самое и с отливами.

Когда Земля, Луна и Солнце находятся на одной линии (Солнце-Земля-Луна или Солнце-Луна-Земля), два основных влияния объединяются, вызывая весенние приливы; когда две силы противостоят друг другу, например, когда угол Луна-Земля-Солнце близок к девяноста градусам, возникают приливы. Когда Луна движется по своей орбите, она меняется с севера от экватора на юг от экватора. Чередование высот приливов становится меньшим, пока они не станут одинаковыми (в момент лунного равноденствия Луна находится над экватором), затем вновь развивается, но с другой полярностью, увеличиваясь до максимальной разницы, а затем снова уменьшаясь.

Текущий

Влияние приливов на течение или поток гораздо труднее анализировать, а данные гораздо труднее собирать. Высота прилива является скалярной величиной и плавно меняется в широком регионе. Поток представляет собой векторную величину с величиной и направлением, которые могут существенно меняться в зависимости от глубины и на коротких расстояниях из-за местной батиметрии. Кроме того, хотя центр водного канала является наиболее полезным местом измерения, моряки возражают, когда оборудование для измерения тока загораживает водные пути. Поток, идущий вверх по изогнутому каналу, может иметь аналогичную величину, даже если его направление непрерывно меняется вдоль канала. Удивительно, но приливы и отливы часто не направлены в противоположные стороны. Направление потока определяется формой восходящего канала, а не формой нисходящего канала. Аналогично, вихри могут образовываться только в одном направлении потока.

Тем не менее, анализ приливных течений аналогичен анализу высоты приливов: в простом случае в данном месте поток паводка движется преимущественно в одном направлении, а отлив - в другом направлении. Скорость паводка имеет положительный знак, а скорость отлива – отрицательный. Анализ продолжается так, как будто это высота прилива.

В более сложных ситуациях основные приливы и отливы не доминируют. Вместо этого направление и величина потока прослеживаются по эллипсу в течение приливного цикла (на полярном графике), а не вдоль линий прилива и отлива. В этом случае анализ может проводиться по парам направлений, при этом основное и вторичное направления расположены под прямым углом. Альтернативой является рассмотрение приливных потоков как комплексных чисел, поскольку каждое значение имеет как величину, так и направление.

Информацию о приливах чаще всего можно увидеть на морских картах , представленных в виде таблицы скоростей течения и направлений с часовыми интервалами, с отдельными таблицами для весенних и приливных приливов. Время соответствует паводку в какой-либо гавани, где характер приливов аналогичен, хотя это может быть и далеко.

Как и в случае с прогнозами высоты прилива, прогнозы приливных потоков, основанные только на астрономических факторах, не учитывают погодные условия, которые могут полностью изменить результат.

Приливный поток через пролив Кука между двумя главными островами Новой Зеландии особенно интересен, поскольку приливы на каждой стороне пролива почти точно не совпадают по фазе, так что паводок на одной стороне совпадает с отливом на другой. В результате возникают сильные течения с почти нулевым изменением высоты прилива в центре пролива. Тем не менее, хотя приливная волна обычно течет в одном направлении в течение шести часов и в обратном направлении в течение шести часов, конкретная волна может длиться восемь или десять часов, при этом обратная волна ослабевает. В особенно суровых погодных условиях обратный нагон можно полностью преодолеть, чтобы поток продолжался в том же направлении в течение трех или более периодов нагона.

Еще одним осложнением режима течения в проливе Кука является то, что прилив на южной стороне (например, в Нельсоне ) следует обычному двухнедельному циклу приливов весна-прилив (как это происходит на западной стороне страны), но характер приливов на северной стороне имеет только один цикл в месяц, как на восточной стороне: Веллингтон и Нейпир .

На графике приливов в проливе Кука отдельно показаны высота и время паводка и отлива до ноября 2007 года; это не измеренные значения, а рассчитываются на основе приливных параметров, полученных на основе измерений многолетней давности. Морская карта пролива Кука предоставляет информацию о приливно-отливных течениях. Например, издание за январь 1979 г. 41 ° 13,9' ю.ш., 174 ° 29,6' в.д. / 41,2317 ° ю.ш., 174,4933 ° в.д. / -41,2317; 174,4933 (к северо-западу от мыса Теравити ) относится к Вестпорту, а номер января 2004 года относится к Веллингтону. Около мыса Теравити в середине пролива Кука изменение высоты прилива практически равно нулю, а приливное течение достигает максимума, особенно вблизи пресловутого Рипа Карори. Помимо погодных эффектов, на фактические течения через пролив Кука влияет разница высот приливов между двумя концами пролива, и, как можно видеть, только один из двух весенних приливов на северо-западном конце пролива возле Нельсона имеет аналогичный весенний прилив в юго-восточной части (Веллингтон), поэтому результирующее поведение не соответствует ни одной эталонной гавани. ^{[ нужна ссылка ]}

Производство электроэнергии

Энергию приливов можно извлечь двумя способами: вставить водяную турбину в приливное течение или построить пруды, которые выпускают/впускают воду через турбину. В первом случае количество энергии полностью определяется временем и величиной приливного течения. Однако лучшие течения могут быть недоступны, поскольку турбины будут мешать судам. Во-вторых, строительство водохранилищ обходится дорого, полностью нарушается естественный круговорот воды, нарушается судоходство. Однако при наличии нескольких прудов электроэнергия может вырабатываться в выбранное время. На сегодняшний день существует несколько установленных систем для производства приливной энергии (наиболее известная из них — La Rance в Сен-Мало , Франция), которые сталкиваются со многими трудностями. Помимо экологических проблем, просто противодействие коррозии и биологическому загрязнению создает инженерные проблемы.

Сторонники приливной энергетики отмечают, что, в отличие от ветроэнергетических систем, уровни генерации можно надежно предсказать, за исключением погодных эффектов. Хотя некоторая генерация возможна в течение большей части приливного цикла, на практике турбины теряют эффективность при более низких рабочих скоростях. Поскольку доступная мощность потока пропорциональна кубу скорости потока, время, в течение которого возможна выработка высокой мощности, короткое.

Приливные течения важны для навигации, и если их не учесть, возникают значительные ошибки в определении местоположения. Высота приливов также важна; например, во многих реках и гаванях у входа есть неглубокая «бара», которая не позволяет лодкам со значительной осадкой заходить во время отлива.

До появления автоматизированной навигации умение рассчитывать приливные эффекты было важно для военно-морских офицеров. В свидетельстве об экзамене для лейтенантов Королевского флота однажды было указано, что будущий офицер способен «изменить ход событий». ^[71]

Время и скорость приливных потоков отображаются на картах приливов или в атласе приливных течений . Карты приливов и отливов поставляются в наборах. Каждая диаграмма охватывает один час между одним паводком и другим (они игнорируют оставшиеся 24 минуты) и показывает средний приливный поток за этот час. Стрелка на карте приливов указывает направление и среднюю скорость течения (обычно в узлах ) для весенних и приливных приливов. Если карта приливов и отливов недоступна, на большинстве морских карт есть « ромбы приливов », которые связывают определенные точки на карте с таблицей, показывающей направление и скорость приливного потока.

Стандартная процедура противодействия приливным воздействиям на навигацию состоит в том, чтобы (1) рассчитать положение « точного счисления » (или DR) на основе расстояния и направления путешествия, (2) отметить карту (вертикальным крестом, похожим на знак плюс) и (3 ) проведите линию от DR по направлению прилива. Расстояние, на которое прилив перемещает лодку вдоль этой линии, вычисляется по скорости прилива, и это дает «расчетное положение» или EP (традиционно обозначается точкой в треугольнике).

Морские карты отображают «нанесенную на карту глубину» воды в определенных местах с помощью « промеров » и использования батиметрических контурных линий для изображения формы подводной поверхности. Эти глубины относятся к « отсчету карты », который обычно представляет собой уровень воды во время самого низкого возможного астрономического прилива (хотя обычно используются и другие данные, особенно исторически, и приливы могут быть ниже или выше по метеорологическим причинам) и, следовательно, являются минимальными глубинами. возможная глубина воды во время приливного цикла. На карте также могут быть показаны «высоты высыхания», которые представляют собой высоту обнаженного морского дна во время самого низкого астрономического прилива.

В таблицах приливов указаны высота и время прилива и отлива воды за каждый день. Чтобы рассчитать фактическую глубину воды, добавьте глубину, указанную на графике, к опубликованной высоте прилива. Глубину в другое время можно определить по приливным кривым, опубликованным для крупных портов. Правило двенадцатых может быть достаточным, если нет точной кривой. Это приближение предполагает, что прирост глубины за шесть часов между маловодьем и паводком составляет: первый час — 1/12, второй — 2/12, третий — 3/12, четвертый — 3/12, пятый — 2/12, шестой — 1/12.

Биологические аспекты

Приливная экология

Приливная экология - это изучение экосистем между линиями низкого и высокого уровня воды вдоль берега. При малой воде приливная зона обнажена (или надводна ), тогда как при высокой воде она находится под водой (или погружена ). приливной зоны Поэтому экологи изучают взаимодействие между приливными организмами и окружающей их средой, а также между различными видами . Наиболее важные взаимодействия могут различаться в зависимости от типа приливного сообщества. Самые широкие классификации основаны на субстрате — каменистом берегу или мягком дне.

Приливные организмы находятся в крайне изменчивой и часто враждебной среде и адаптировались, чтобы справляться с этими условиями и даже использовать их. Одной из легко заметных особенностей является вертикальная зональность , при которой сообщество делится на отдельные горизонтальные полосы конкретных видов на каждой высоте над уровнем воды. Способность вида справляться с высыханием определяет его верхний предел, а конкуренция с другими видами устанавливает его нижний предел.

Люди используют приливные зоны для еды и отдыха. Чрезмерная эксплуатация может нанести непосредственный ущерб приливным зонам. Другие антропогенные действия, такие как внедрение инвазивных видов и изменение климата, имеют серьезные негативные последствия. Морские охраняемые территории – это один из вариантов, который сообщества могут использовать для защиты этих территорий и оказания помощи научным исследованиям .

Биологические ритмы

Приблизительно 12-часовой и двухнедельный приливный цикл оказывает большое влияние на приливно-отливную зону. ^[72] и морские организмы. ^[73] Следовательно, их биологические ритмы имеют тенденцию повторяться примерно в несколько раз этих периодов. ^[74] Многие другие животные, например позвоночные , демонстрируют сходные циркадные ритмы. ^[75] Примеры включают беременность и вылупление яиц. У людей менструальный цикл длится примерно лунный месяц , что даже кратно периоду приливов. Подобные параллели, по крайней мере, намекают на общее происхождение всех животных от морского предка. ^[76]

Другие приливы

Когда колеблющиеся приливные течения в стратифицированном океане текут по неровному рельефу дна, они генерируют внутренние волны с приливными частотами. Такие волны называются внутренними приливами .

На мелководье в открытой воде могут возникать вращающиеся приливные течения, текущие в направлениях, которые постоянно меняются, и, таким образом, направление потока (а не поток) совершает полный оборот в 12 + 1 / 2 часа (например, Нантакет Шолс ). ^[77]

Помимо океанических приливов, большие озера могут испытывать небольшие приливы, и даже планеты могут испытывать атмосферные приливы и земные приливы . Это континуальные механические явления. Первые два происходят в жидкостях . кору Земли Третий влияет на тонкую твердую , окружающую ее полужидкую недра (с различными модификациями).

Озерные приливы

В больших озерах, таких как Верхнее и Эри, могут наблюдаться приливы от 1 до 4 см (от 0,39 до 1,6 дюйма), но они могут быть замаскированы метеорологическими явлениями, такими как сейш . ^[78] Уровень прилива в озере Мичиган составляет от 1,3 до 3,8 см (от 0,5 до 1,5 дюйма). ^[79] или см ( 1 + 3/4 дюйма 4,4 ). ^[80] Это настолько мало, что другие более крупные эффекты полностью маскируют любой прилив, и поэтому эти озера считаются неприливными. ^[81]

Атмосферные приливы

Атмосферные приливы незначительны на уровне земли и на высотах полета, маскируясь . гораздо более важными воздействиями погоды Атмосферные приливы имеют как гравитационное, так и тепловое происхождение и представляют собой доминирующую динамику на расстоянии примерно от 80 до 120 километров (от 50 до 75 миль), выше которых молекулярная плотность становится слишком низкой, чтобы поддерживать поведение жидкости.

Земные приливы

Земные приливы или земные приливы воздействуют на всю массу Земли, которая действует подобно жидкому гироскопу с очень тонкой корой. Земная кора смещается (внутрь/наружу, восток/запад, север/юг) в ответ на лунную и солнечную гравитацию, океанские приливы и атмосферную нагрузку. Полусуточная амплитуда земных приливов, хотя и незначительная для большинства видов человеческой деятельности, может достигать около 55 сантиметров (22 дюйма) на экваторе - 15 сантиметров (5,9 дюйма) из-за Солнца - что важно для калибровки GPS и измерений VLBI . Точные астрономические угловые измерения требуют знания скорости вращения Земли и движения полюсов , на оба из которых влияют земные приливы. Полусуточные земные приливы M ₂ почти совпадают с фазой Луны с задержкой около двух часов. ^{[ нужна ссылка ]}

Галактические приливы

Галактические приливы — это приливные силы, действующие галактиками на звезды внутри них и на галактики-спутники, вращающиеся вокруг них. Считается, что воздействие галактического прилива на Солнечной системе в облако Оорта является причиной 90 процентов долгопериодических комет. ^[82]

Неправильные термины

Цунами , большие волны, возникающие после землетрясений, иногда называют приливными волнами , но это название дано из-за их сходства с приливом, а не какой-либо причинно-следственной связи с приливом. Другими явлениями, не связанными с приливами, но использующими слово «прилив», являются отлив , штормовой прилив , ураганный прилив и черные или красные приливы . Многие из этих обычаев являются историческими и относятся к более раннему значению слова «прилив» как «часть времени, сезон» и «поток, течение или наводнение». ^[83]

См. также

Аквакультура - Выращивание водных организмов.
Теорема Клеро – Теорема о гравитации
Береговая эрозия - перемещение земель вдоль береговой линии.
Создание порта
Наступление прилива , также известное как прилив или предел прилива – самая дальняя точка вверх по течению, где река подвергается воздействию приливных колебаний.
Функция Хафа - собственные функции приливных уравнений Лапласа, которые управляют движением жидкости на вращающейся сфере.
Королевский прилив - особенно высокий весенний прилив.
Эксперимент по лунной лазерной локации – измерение расстояния между Землей и Луной с помощью лазерного луча.
Лунная фаза - форма освещенной части Луны, если смотреть с Земли.
Возвышенный пляж , также известный как Морская терраса – возникшая прибрежная форма рельефа.
Средний паводок — уровень воды, от которого измеряются глубины, отображаемые на морской карте.
Среднее межень – уровень воды, от которого измеряются глубины, отображаемые на морской карте.
Орбита Луны – обращение Луны вокруг Земли.
Примитивные уравнения - уравнения для аппроксимации глобального атмосферного потока.
Приливный заграждение - структура, похожая на плотину.
Приливный остров - остров, до которого можно добраться пешком во время отлива.
Приливная блокировка - ситуация, в которой период обращения астрономического объекта совпадает с периодом его вращения.
Приливная призма - объем воды в устье или заливе между средним приливом и средним отливом.
Приливный резонанс - усиленный прилив из-за резонанса океана.
Приливная река - река, на течение и уровень которой влияют приливы.
Генератор приливных потоков - тип технологии производства приливной энергии.
Приливное возникновение землетрясений - идея о том, что приливные силы могут вызывать сейсмичность.
Приливный бассейн - каменистый бассейн на берегу моря, отделенный от моря во время отлива и наполненный морской водой.
Линия прилива – место, где сходятся два океанских течения.
Приливы в окраинных морях - Динамика деформации приливных волн на мелководье окраинных морей.

Примечания

^ Береговая ориентация и геометрия влияют на фазу, направление и амплитуду амфидромных систем , прибрежных волн Кельвина , а также резонансных сейш в заливах. В эстуариях сезонные речные оттоки влияют на приливные потоки.
^ В таблицах приливов обычно указываются средний нижний межень (mllw, среднее значение среднего нижнего межень за 19 лет), средний высокий межень (mhlw), средний нижний паводок (mlhw), средний высокий паводок (mhhw), а также перигейские приливы . Это средние значения в том смысле, что они выводятся из средних данных. ^[5]
^ «Луна, как ближайшее к Земле небесное тело, наиболее обильно изливает свое влияние на мирские предметы, ибо большинство из них, одушевленных и неодушевленных, сочувствуют ей и изменяются в компании с ней; реки увеличиваются и уменьшаются потоки с ее светом, моря поворачивают свои собственные волны с ее подъемом и заходом...» ^[18]
^ "Orbis virtutistractiæ, quæ est in Luna, porrigitur utque ad Terras и prolectat aquas sub Zonam Torridam, ... Celerite vero luna transvolante vertex, cum aquae tam cequi sequi non possint, flux quidem fit Oceani sub Torrida in Occidentem, . . (Сфера подъемной силы, которая [центрирована] в Луне, простирается до земли и притягивает воды под жаркую зону... Однако луна быстро летит через зенит; потому что воды не может следовать так быстро, прилив океана под жаркой [зоной] действительно направлен на запад...» ^[26]
^ См., например, в «Началах» (книга 1) (перевод 1729 г.), следствия 19 и 20 к предложению 66, на страницах 251–254 , со ссылкой на страницу 234 и последующие; и в книге 3 предложения 24, 36 и 37, начиная со стр. 255 .
^ По данным НАСА, лунная приливная сила в 2,21 раза превышает солнечную.
^ См . «Приливная сила – Математическая обработка и цитируемые там источники».
^ «Океан не вызывает приливов в качестве прямой реакции на вертикальные силы в выпуклостях. Приливная сила составляет всего лишь около 1 десятимиллионной размера гравитационной силы из-за гравитации Земли. Это горизонтальная составляющая приливной силы. это вызывает приливную выпуклость, заставляющую жидкость сходиться в подлунной и антиподальной точках и двигаться от полюсов, вызывая там сокращение». (...) «Проекция приливной силы на горизонтальное направление называется силой тяги (см. Кнаусс, рис. 10.11). Эта сила вызывает ускорение воды к подлунной и антиподальной точкам, наращивая воду до тех пор, пока давление Градиентная сила от выпуклой морской поверхности точно уравновешивает поле тяговых сил». ^[52]
^ «Хотя солнечная и лунная оболочки считаются реальными водами океана, необходимо признать еще один очень важный фактор. Компоненты сил, генерирующих приливы, действующие по касательной вдоль водной поверхности, оказываются наиболее важными. Точно так же, как ведро с водой легче скользить по полу, чем поднимать его, горизонтальные тяговые компоненты перемещают воду к точкам, находящимся непосредственно под солнцем или луной и вдали от них, гораздо эффективнее, чем вертикальные компоненты могут поднять ее. силы несут наибольшую ответственность за попытки сформироватьокеан в симметричные яйцеобразные расширения (потенциал прилива, равновесный прилив). Они достигают своего максимума в кольцах под углом 45° от точек, находящихся непосредственно под солнцем или луной и вдали от них». ^[53]
^ «... гравитационный эффект, вызывающий приливы, слишком слаб, чтобы поднять океаны на 12 дюймов по вертикали от земли. Однако возможно переместить океаны горизонтально в пределах гравитационного поля Земли. Это собирает океаны по направлению к две точки, где высота воды увеличивается из-за сходящегося объема воды». ^[54]
^ В настоящее время сутки удлиняются со скоростью около 0,002 секунды за столетие. ^[58]
^ Для демонстрации этой домашней страницы Tides предлагается образец высоты прилива, преобразованный в звуковой файл .mp3 , и насыщенный звук сильно отличается от чистого тона.

Ссылки

^ Редди, MPM и Аффхолдер, М. (2002). Описательная физическая океанография: современное состояние . Тейлор и Фрэнсис . п. 249. ИСБН 90-5410-706-5 . OCLC 223133263 . Архивировано из оригинала 16 сентября 2023 г. Получено 5 января 2022 г. - через Google Книги .
^ Хаббард, Ричард (1893). Boater's Bowditch: Американский практический штурман для небольших судов . МакГроу-Хилл Профессионал. п. 54. ИСБН 0-07-136136-7 . OCLC 44059064 . Архивировано из оригинала 16 сентября 2023 г. Получено 5 января 2022 г. - через Google Книги .
^ «Приливный лунный день» . НОАА . Архивировано из оригинала 17 августа 2018 г. Проверено 7 апреля 2007 г. Не путайте с астрономическими лунными сутками на Луне. Лунный зенит – это самая высокая точка Луны на небе.
^ Меллор, Джордж Л. (1996). Введение в физическую океанографию . Спрингер. п. 169. ИСБН 1-56396-210-1 .
^ «Глоссарий прибрежной терминологии: H – M» . Вашингтонский департамент экологии , штат Вашингтон. Архивировано из оригинала 21 ноября 2017 года . Проверено 5 апреля 2007 г.
^ «Определения приливных терминов» . Информация о земле Новая Зеландия . Архивировано из оригинала 30 августа 2014 года . Проверено 20 февраля 2017 г.
^ «Океанские приливы и магнитные поля» . Студия визуализации НАСА . НАСА . 30 декабря 2016 г. Архивировано из оригинала 27 ноября 2020 г. . Проверено 20 ноября 2020 г.
^ «Типы и причины приливных циклов» . Национальная океаническая служба Национального управления океанических и атмосферных исследований США (НОАА) (раздел образования). Архивировано из оригинала 1 февраля 2012 года.
^ Свердлов, Ноэль М.; Нойгебауэр, Отто (1984). Математическая астрономия в «О революции» Коперника . Том 1. Спрингер Верлаг. п. 76. ИСБН 0-387-90939-7 . Архивировано из оригинала 16 сентября 2023 г. Получено 22 ноября 2020 г. - через Google Книги .
^ Jump up to: ^а ^б Харрис, Д.Л. (1981). Приливы и данные о приливах в Соединенных Штатах . Специальный репортаж (Центр прибрежных инженерных исследований (США))). Инженерный корпус армии США , Исследовательский центр прибрежной инженерии. п. 32. Архивировано из оригинала 16 сентября 2023 г. Получено 24 августа 2021 г. - через Google Книги .
^ "neap²". Оксфордский словарь английского языка (2-е изд.). Издательство Оксфордского университета . 1989. Древнеанглийский (пример, приведенный в 469 году нашей эры: forðganges nip – без возможности продвижения). Датский ниптид, вероятно, произошел от английского. Английский термин «neap-flood» (от которого происходит «neap tide»), по-видимому, стал широко использоваться к 725 году нашей эры.
^ «Что такое перигейский весенний прилив?» . Национальное управление океанических и атмосферных исследований. 26 февраля 2021 года. Архивировано из оригинала 30 июля 2021 года . Проверено 16 июля 2021 г.
^ Ле Провост, Кристиан (1991). «Генерация приливов и сложных приливов (обзор)». В Паркер, Брюс Б. (ред.). Приливная гидродинамика . Джон Уайли и сыновья . ISBN 978-0-471-51498-5 .
^ Аккад, Ю. и Пекерис, К.Л. (28 ноября 1978 г.). «Решение приливных уравнений для приливов M ₂ и S ₂ в Мировом океане на основе знания только приливного потенциала». Философские труды Лондонского королевского общества А. 290 (1368): 235–266. Бибкод : 1978RSPTA.290..235A . дои : 10.1098/rsta.1978.0083 . S2CID 119526571 .
^ «Прогноз приливов» . Новая Зеландия: Национальный институт исследований воды и атмосферы. Архивировано из оригинала 14 октября 2008 г. Проверено 7 ноября 2008 г. Включая анимацию приливов M2, S2 и K1 для Новой Зеландии.
^ Марчук, Гури И.; Каган, бакалавр наук (6 декабря 2012 г.). Динамика океанских приливов . Спрингер. ISBN 9789400925717 . Архивировано из оригинала 16 сентября 2023 года . Проверено 22 ноября 2020 г. - через Google Книги .
^ Шуреман, Пол (1971). Руководство по гармоническому анализу и прогнозированию приливов и отливов . Побережье США и геодезическая съемка. п. 204. Архивировано из оригинала 8 августа 2017 г. Проверено 14 января 2018 г.
^ Птолемей (1940). «2». Тетрабиблос . Том. 1. Перевод Роббинса, Фрэнка Э. Кембриджа, Массачусетс: Издательство Гарвардского университета .
^ Беде (1999). Расчёт времени . Перевод Уоллис, Фейт. Издательство Ливерпульского университета . п. 82. ИСБН 0-85323-693-3 . Архивировано из оригинала 9 апреля 2023 года . Проверено 1 июня 2018 г. - через Google Книги .
^ Беде 1999 , стр. 83.
^ Jump up to: ^а ^б Беде 1999 , стр. 84.
^ Jump up to: ^а ^б Беде 1999 , стр. 85.
^ Jump up to: ^а ^б ^с ^д Толмачева, Марина (2014). Глик, Томас Ф. (ред.). География, Хорография . Рутледж . п. 188. ИСБН 978-1135459321 . {{cite book}}: |work= игнорируется ( помогите )
^ «Саймон Стевин» (PDF) (pdf) (на голландском языке). Фландрийский морской институт. Архивировано (PDF) из оригинала 5 августа 2014 г. Проверено 1 июня 2014 г.
^ Пальмерино, Карла Рита; Тийссен, JMMH (31 августа 2004 г.). Рецепция галилеевой науки о движении в Европе семнадцатого века . Springer Science+Business Media . п. 200. ИСБН 978-1-4020-2455-9 . Архивировано из оригинала 12 апреля 2022 года . Проверено 29 ноября 2022 г. - через Google Книги .
^ Иоганн Кеплер, Astronomia nova ... (1609), с. 5 Introductio in hoc opus (Введение к данной работе). Со страницы 5:
^ Jump up to: ^а ^б Лисицын, Е. (1974). "2 "Периодические изменения уровня моря: Астрономические приливы" ". Изменения уровня моря (Серия Elsevier Oceanography) . Том. 8. с. 5.
^ «Что вызывает приливы?» . США Национальная океаническая служба Национального управления океанических и атмосферных исследований (НОАА) (раздел образования). Архивировано из оригинала 20 августа 2016 г. Проверено 6 сентября 2009 г.
^ Вар, Дж. (1995). Земные приливы в «Глобальной физике Земли», Справочная полка № 1 Американского геофизического союза . стр. 40–46.
^ Эйлер, Леонард ; Эйтон, Эрик Дж. (1996). Механические и астрономические наблюдения, относящиеся к физике . Springer Science+Business Media . стр. 19–. ISBN 978-3-7643-1459-0 – через Google Книги .
^ Томсон, Томас , изд. (март 1819 г.). «О рассказе капитана Кука о приливах» . Анналы философии . ХIII . Лондон: Болдуин, Крэдок и Джой: 204. Архивировано из оригинала 26 августа 2016 года . Проверено 25 июля 2015 г.
^ Jump up to: ^а ^б Цзошэн, Ю.; Эмери, нокаут и Юи, X. (июль 1989 г.). «Историческое развитие и использование тысячелетних таблиц прогнозирования приливов» . Лимнология и океанография . 34 (5): 953–957. Бибкод : 1989LimOc..34..953Z . дои : 10.4319/lo.1989.34.5.0953 .
^ Картрайт, Дэвид Э. (1999). Приливы: научная история . Кембридж, Великобритания: Издательство Кембриджского университета . ISBN 9780521621458 .
^ Кейс, Джеймс (март 2000 г.). «Понимание приливов - от древних верований к современным решениям уравнений Лапласа». СИАМ Новости . 33 (2).
^ Дудсон, А.Т. (декабрь 1921 г.). «Гармоническое развитие приливно-генерирующего потенциала» . Труды Лондонского королевского общества А. 100 (704): 305–329. Бибкод : 1921RSPSA.100..305D . дои : 10.1098/rspa.1921.0088 .
^ Казотто С. и Бискани Ф. (апрель 2004 г.). «Полностью аналитический подход к гармоническому развитию приливно-генерирующего потенциала с учетом прецессии, нутации и возмущений, вызванных фигурными и планетарными условиями». Отделение ААН по динамической астрономии . 36 (2): 67. Бибкод : 2004DDA....35.0805C .
^ Мойер, Т.Д. (2003). Формулировка наблюдаемых и вычисленных значений типов данных Deep Space Network для навигации (PDF) . Связь и навигация в дальнем космосе. Том. 3. Уайли . стр. 126–128. ISBN 0-471-44535-5 . Архивировано из оригинала (PDF) 16 октября 2004 г.
^ Flussi e reflux [ Приливы и отливы ] (на итальянском языке). Милан: Фельтринелли. 2003. ISBN 88-07-10349-4 .
^ ван дер Варден, БЛ (1987). «Гелиоцентрическая система в греческой, персидской и индуистской астрономии». Анналы Нью-Йоркской академии наук . 500 (1): 525–545 [527]. Бибкод : 1987NYASA.500..525V . дои : 10.1111/j.1749-6632.1987.tb37224.x . S2CID 222087224 .
^ Картрайт, Делавэр (1999). «Приливы, научная история» . Эос-транзакции . 80 (36): 11, 18. Бибкод : 1999EOSTr..80..408A . дои : 10.1029/99EO00304 .
^ «Аборигенная астрономия предсказывает влияние Луны на приливы и отливы до Галилея и Ньютона» (на бразильском португальском языке). 19 июня 2009 г. Проверено 11 декабря 2021 г.
^ «Машина для предсказания приливов Дудсона-Леже» . Океанографическая лаборатория Праудмана. Архивировано из оригинала 20 марта 2009 г. Проверено 3 октября 2008 г.
^ Лаббок, JW (1831 г.). «О приливах у берегов Великобритании» . Философский журнал . 9 (53): 333–335. дои : 10.1080/14786443108647618 .
^ Уэвелл, Уильям (1836). «Исследования о приливах, серия шестая. О результатах обширной системы приливных наблюдений, произведенных на побережьях Европы и Америки в июне 1835 года» . Философские труды Лондонского королевского общества . 126 : 289–341.
^ Хьюитт, Уильям (1841). «Приливно-отливные наблюдения в Северном море» . Морской журнал : 180–183.
^ Картрайт, Дэвид Эдгар (17 августа 2000 г.). Приливы: научная история . Издательство Кембриджского университета . ISBN 978-0-521-79746-7 . OCLC 1001932580 .
^ Кучер, Джеральд Дж.; Вудленд, Бертрам Г.; Бродхерст, Фредерик М. (1 сентября 1990 г.). «Свидетельства отложений в результате отдельных приливов и приливных циклов из сланцев Фрэнсис-Крик (вмещающая порода биоты Мейзон-Крик), Вестфальский период D (Пенсильвания), северо-восточный Иллинойс» . Осадочная геология . 68 (3): 211–221. Бибкод : 1990SedG...68..211K . дои : 10.1016/0037-0738(90)90113-8 . ISSN 0037-0738 .
^ Арчер, Аллен В.; Кучер, Джеральд Дж; Квале, Эрик П. (1995). «Роль асимметрии приливных скоростей в отложении илистых приливных ритмитов (каменноугольный период, Восточный внутренний угольный бассейн, США)» . Журнал SEPM осадочных исследований . 65 : 408–416. doi : 10.1306/d42680d6-2b26-11d7-8648000102c1865d .
^ Янг, Калифорния (1889 г.). Учебник общей астрономии (PDF) . п. 288. Архивировано (PDF) из оригинала 05 октября 2019 г. Проверено 13 августа 2018 г.
^ «Межпланетный отлив» . Управление научной миссии . 03.05.2000. Архивировано из оригинала 4 июня 2023 г. Проверено 25 июня 2023 г.
^ «Равновесный прилив» . Глоссарий АМС . 2020-09-02. Архивировано из оригинала 01 августа 2020 г. Проверено 2 сентября 2020 г.
^ Томпсон, ЛуЭнн (2006). «Физические процессы в океане» (PDF) . Архивировано (PDF) из оригинала 28 сентября 2020 г. Проверено 27 июня 2020 г.
^ Хикс, С.Д. (2006). Понимание приливов (PDF) (Отчет). НОАА . Архивировано (PDF) из оригинала 20 января 2022 г. Проверено 2 сентября 2020 г.
^ Маккалли, Джеймс Грейг (2006). За Луной: разговорное руководство по здравому смыслу для понимания приливов, World Scientific . Всемирная научная. ISBN 9789814338189 . Архивировано из оригинала 16 сентября 2023 г. Получено 5 января 2022 г. - через Google Книги .
^ «Что учителя физики ошибаются в отношении приливов! - PBS Space Time» . PBS LearningMedia . 17.06.2020. Архивировано из оригинала 21 октября 2020 г. Проверено 27 июня 2020 г.
^ Мунк, В.; Вунш, К. (1998). «Бездные рецепты II: энергетика смешения приливов и ветров». Глубоководные исследования . Часть I. 45 (12): 1977. Бибкод : 1998DSRI...45.1977M . дои : 10.1016/S0967-0637(98)00070-3 .
^ Рэй, РД; Инес, Р.Дж.; Чао, Б.Ф. (1996). «Обнаружение приливной диссипации в твердой Земле с помощью спутникового слежения и альтиметрии». Природа . 381 (6583): 595. Бибкод : 1996Natur.381..595R . дои : 10.1038/381595a0 . S2CID 4367240 .
^ Лекция 2: Роль приливной диссипации и приливные уравнения Лапласа Мирла Хендершотта. Том GFD Proceedings, 2004 г., примечания WHOI Ярона Толедо и Маршалла Уорда.
^ «карта, показывающая мировое распределение режимов приливов: полусуточных, суточных и смешанных полусуточных» . США Национальное управление океанических и атмосферных исследований (NOAA), Национальная океаническая служба (раздел образования) . Архивировано из оригинала 27 августа 2018 г. Проверено 5 сентября 2009 г.
^ Турман, Х.В. (1994). Вводная океанография (7-е изд.). Нью-Йорк: Издательство Macmillan . стр. 252–276. ссылка
^ Росс, Д.А. (1995). Введение в океанографию . Нью-Йорк: ХарперКоллинз . стр. 236–242.
^ Витце, Александра (5 июля 2020 г.). «Как люди меняют приливы и отливы океанов» . BBC Будущее . Би-би-си . Архивировано из оригинала 6 июля 2020 года . Проверено 8 июля 2020 г.
^ «Глоссарий метеорологии» . Американское метеорологическое общество . Архивировано из оригинала 08 мая 2021 г. Проверено 2 апреля 2021 г.
^ Вебстер, Томас (1837). Элементы физики . Напечатано для Скотта, Вебстера и Гири. п. 168 .
^ "ЧАСТО ЗАДАВАЕМЫЕ ВОПРОСЫ" . Архивировано из оригинала 12 февраля 2012 года . Проверено 23 июня 2007 г.
^ Jump up to: ^а ^б О'Рейли, CTR; Солвасон, Рон и Соломон, Кристиан (2005). Райан, Дж. (ред.). «Где самые большие приливы в мире». Годовой отчет BIO «Обзор 2004 года» . Вашингтон, округ Колумбия: Биотехнологии. Индийская организация: 44–46.
^ Jump up to: ^а ^б О'рейли, Чарльз Т.; Солвасон, Рон; Соломон, Кристиан (2005). «Решение крупнейших приливов в мире» (PDF) . В Перси, JA; Эванс, Эй Джей; Уэллс, П.Г.; Ролстон, С.Дж. (ред.). Меняющийся залив Фанди - за 400 лет, Материалы 6-го семинара по заливу Фанди, Корнуоллис, Новая Шотландия, 29 сентября 2004 г. - 2 октября 2004 г. Окружающая среда Канады - Атлантический регион, Периодический отчет №. 23. Дартмут, Северная Каролина и Саквилл, Северная Каролина . Архивировано (PDF) из оригинала 27 августа 2016 г. Проверено 1 апреля 2013 г.
^ Пингри, РД; Мэддок, Л. (1978). «Глубоководные исследования». 25 : 53–63. {{cite journal}}: Для цитирования журнала требуется |journal= ( помощь )
^ Центр оперативной океанографической продукции и услуг, Национальная океаническая служба, Национальное управление океанических и атмосферных исследований (январь 2000 г.). «Глоссарий приливов и течений» (PDF) . Силвер Спринг, Мэриленд. Архивировано (PDF) из оригинала 28 января 2007 г. Проверено 5 апреля 2007 г. {{cite web}}: CS1 maint: несколько имен: список авторов ( ссылка )
^ «Гармонические составляющие» . НОАА . Архивировано из оригинала 17 марта 2007 г. Проверено 5 апреля 2007 г.
^ Общество морских исследований (1958). Зеркало моряка . Архивировано из оригинала 16 сентября 2023 г. Проверено 28 апреля 2009 г. - через Google Книги .
^ Бос, Арканзас; Гуманао, Г.С.; ван Катвейк, ММ; Мюллер, Б.; Саседа, ММ и Техада, РП (2011). «Онтогенетическое изменение среды обитания, рост популяции и роющее поведение индо-тихоокеанской пляжной звезды Archaster typicus (Echinodermata: Asteroidea)» . Морская биология . 158 (3): 639–648. Бибкод : 2011МарБи.158..639B . дои : 10.1007/s00227-010-1588-0 . ПМЦ 3873073 . ПМИД 24391259 .
^ Бос, А.Р. и Гуманао, Г.С. (2012). «Лунный цикл определяет наличие коралловых рифовых рыб на рыбных рынках». Журнал биологии рыб . 81 (6): 2074–2079. Бибкод : 2012JFBio..81.2074B . дои : 10.1111/j.1095-8649.2012.03454.x . ПМИД 23130702 .
^ Нэйлор, Эрнест (4 февраля 2010 г.). «Глава 5: Лунные и полулунные биоритмы». Хронобиология морских организмов . Издательство Кембриджского университета . ISBN 978-1-139-48494-7 . Архивировано из оригинала 16 сентября 2023 г. Проверено 3 января 2022 г. - через Google Книги .
^ Чжу, Бокай; Даксо, Клиффорд К.; О'Мэлли, Берт В. (01 июля 2018 г.). «Открытие «Musica Universalis» клетки: краткая история биологических 12-часовых ритмов» . Журнал Эндокринного общества . 2 (7): 727–752. дои : 10.1210/js.2018-00113 . ISSN 2472-1972 . ПМК 6025213 . ПМИД 29978151 . Архивировано из оригинала 16 сентября 2023 г. Проверено 03 января 2022 г.
^ Дарвин, Чарльз (1871). Происхождение человека и отбор по признаку пола . Лондон: Джон Мюррей.
^ Ле Лашер, Эмбер А. (апрель 1924 г.). «Приливные течения в открытом море: подземные приливные течения на легком судне Нантакет Шолс» . Географическое обозрение . 14 (2): 282–286. Бибкод : 1924GeoRv..14..282L . дои : 10.2307/208104 . JSTOR 208104 . Архивировано из оригинала 16 сентября 2023 года . Проверено 4 февраля 2012 г.
^ «Есть ли на Великих озерах приливы?» . Информационная сеть Великих озер. 1 октября 2000 г. Архивировано из оригинала 30 декабря 2017 г. Проверено 10 февраля 2010 г.
^ Колдер, Винс. «Приливы на озере Мичиган» . Аргоннская национальная лаборатория. Архивировано из оригинала 15 августа 2019 г. Проверено 14 августа 2019 г.
^ Данкерсон, Дуэйн. «Луна и приливы» . Астрономия Коротко. Архивировано из оригинала 15 января 2010 г. Проверено 10 февраля 2010 г.
^ «Есть ли на Великих озерах приливы?» . Национальная океаническая служба . НОАА . Архивировано из оригинала 23 апреля 2016 г. Проверено 26 апреля 2016 г.
^ Нурми, П.; Валтонен, MJ и Чжэн, JQ (2001). «Периодические изменения потока Облака Оорта и воздействия комет на Землю и Юпитер» . Ежемесячные уведомления Королевского астрономического общества . 327 (4): 1367–1376. Бибкод : 2001MNRAS.327.1367N . дои : 10.1046/j.1365-8711.2001.04854.x .
^ "прилив". Оксфордский словарь английского языка . Том. XVIII (2-е изд.). Издательство Оксфордского университета . 1989. с. 64.

Дальнейшее чтение

150 лет приливов на западном побережье: самая длинная серия приливных наблюдений в Америке. Архивировано 5 мая 2011 г. в Wayback Machine NOAA (2004).
Евгений Бутиков: Динамичная картина океанских приливов. Архивировано 11 сентября 2008 г. в Wayback Machine.
Приливы и центробежная сила. Архивировано 12 мая 2007 г. в Wayback Machine : Почему центробежная сила не объясняет противоположную долю прилива (с красивой анимацией).
О. Толедано и др. (2008): Приливы в асинхронных двоичных системах. Архивировано 9 августа 2017 г. в Wayback Machine.
Гейлорд Джонсон «Как Луна и Солнце вызывают приливы». Архивировано 16 сентября 2023 г. в журнале Wayback Machine Popular Science , апрель 1934 г.

Саймон, Бернард (2013) [2007]. Прибрежные приливы . Перевод Мэнли, Дэвид. Океанографический институт, Фонд Альберта I, принца Монако . ISBN 978-2-903581-83-1 . Архивировано из оригинала 13 ноября 2022 г. Проверено 18 октября 2021 г.

Внешние ссылки

[3] Береговая ориентация и геометрия влияют на фазу, направление и амплитуду амфидромных систем , прибрежных волн Кельвина , а также резонансных сейш в заливах. В эстуариях сезонные речные оттоки влияют на приливные потоки.

[7] В таблицах приливов обычно указываются средний нижний межень (mllw, среднее значение среднего нижнего межень за 19 лет), средний высокий межень (mhlw), средний нижний паводок (mlhw), средний высокий паводок (mhhw), а также перигейские приливы . Это средние значения в том смысле, что они выводятся из средних данных. ^[5]

[21] «Луна, как ближайшее к Земле небесное тело, наиболее обильно изливает свое влияние на мирские предметы, ибо большинство из них, одушевленных и неодушевленных, сочувствуют ей и изменяются в компании с ней; реки увеличиваются и уменьшаются потоки с ее светом, моря поворачивают свои собственные волны с ее подъемом и заходом...» ^[18]

[30] "Orbis virtutistractiæ, quæ est in Luna, porrigitur utque ad Terras и prolectat aquas sub Zonam Torridam, ... Celerite vero luna transvolante vertex, cum aquae tam cequi sequi non possint, flux quidem fit Oceani sub Torrida in Occidentem, . . (Сфера подъемной силы, которая [центрирована] в Луне, простирается до земли и притягивает воды под жаркую зону... Однако луна быстро летит через зенит; потому что воды не может следовать так быстро, прилив океана под жаркой [зоной] действительно направлен на запад...» ^[26]

[33] См., например, в «Началах» (книга 1) (перевод 1729 г.), следствия 19 и 20 к предложению 66, на страницах 251–254 , со ссылкой на страницу 234 и последующие; и в книге 3 предложения 24, 36 и 37, начиная со стр. 255 .

[55] По данным НАСА, лунная приливная сила в 2,21 раза превышает солнечную.

[56] См . «Приливная сила – Математическая обработка и цитируемые там источники».

[60] «Океан не вызывает приливов в качестве прямой реакции на вертикальные силы в выпуклостях. Приливная сила составляет всего лишь около 1 десятимиллионной размера гравитационной силы из-за гравитации Земли. Это горизонтальная составляющая приливной силы. это вызывает приливную выпуклость, заставляющую жидкость сходиться в подлунной и антиподальной точках и двигаться от полюсов, вызывая там сокращение». (...) «Проекция приливной силы на горизонтальное направление называется силой тяги (см. Кнаусс, рис. 10.11). Эта сила вызывает ускорение воды к подлунной и антиподальной точкам, наращивая воду до тех пор, пока давление Градиентная сила от выпуклой морской поверхности точно уравновешивает поле тяговых сил». ^[52]

[62] «Хотя солнечная и лунная оболочки считаются реальными водами океана, необходимо признать еще один очень важный фактор. Компоненты сил, генерирующих приливы, действующие по касательной вдоль водной поверхности, оказываются наиболее важными. Точно так же, как ведро с водой легче скользить по полу, чем поднимать его, горизонтальные тяговые компоненты перемещают воду к точкам, находящимся непосредственно под солнцем или луной и вдали от них, гораздо эффективнее, чем вертикальные компоненты могут поднять ее. силы несут наибольшую ответственность за попытки сформироватьокеан в симметричные яйцеобразные расширения (потенциал прилива, равновесный прилив). Они достигают своего максимума в кольцах под углом 45° от точек, находящихся непосредственно под солнцем или луной и вдали от них». ^[53]

[64] «... гравитационный эффект, вызывающий приливы, слишком слаб, чтобы поднять океаны на 12 дюймов по вертикали от земли. Однако возможно переместить океаны горизонтально в пределах гравитационного поля Земли. Это собирает океаны по направлению к две точки, где высота воды увеличивается из-за сходящегося объема воды». ^[54]

[69] В настоящее время сутки удлиняются со скоростью около 0,002 секунды за столетие. ^[58]

[80] Для демонстрации этой домашней страницы Tides предлагается образец высоты прилива, преобразованный в звуковой файл .mp3 , и насыщенный звук сильно отличается от чистого тона.

[Reddy-1] Редди, MPM и Аффхолдер, М. (2002). Описательная физическая океанография: современное состояние . Тейлор и Фрэнсис . п. 249. ИСБН 90-5410-706-5 . OCLC 223133263 . Архивировано из оригинала 16 сентября 2023 г. Получено 5 января 2022 г. - через Google Книги .

[Hubbard-2] Хаббард, Ричард (1893). Boater's Bowditch: Американский практический штурман для небольших судов . МакГроу-Хилл Профессионал. п. 54. ИСБН 0-07-136136-7 . OCLC 44059064 . Архивировано из оригинала 16 сентября 2023 г. Получено 5 января 2022 г. - через Google Книги .

[4] «Приливный лунный день» . НОАА . Архивировано из оригинала 17 августа 2018 г. Проверено 7 апреля 2007 г. Не путайте с астрономическими лунными сутками на Луне. Лунный зенит – это самая высокая точка Луны на небе.

[5] Меллор, Джордж Л. (1996). Введение в физическую океанографию . Спрингер. п. 169. ИСБН 1-56396-210-1 .

[6] «Глоссарий прибрежной терминологии: H – M» . Вашингтонский департамент экологии , штат Вашингтон. Архивировано из оригинала 21 ноября 2017 года . Проверено 5 апреля 2007 г.

[8] «Определения приливных терминов» . Информация о земле Новая Зеландия . Архивировано из оригинала 30 августа 2014 года . Проверено 20 февраля 2017 г.

[NASA2016-9] «Океанские приливы и магнитные поля» . Студия визуализации НАСА . НАСА . 30 декабря 2016 г. Архивировано из оригинала 27 ноября 2020 г. . Проверено 20 ноября 2020 г.

[noaa7-10] «Типы и причины приливных циклов» . Национальная океаническая служба Национального управления океанических и атмосферных исследований США (НОАА) (раздел образования). Архивировано из оригинала 1 февраля 2012 года.

[11] Свердлов, Ноэль М.; Нойгебауэр, Отто (1984). Математическая астрономия в «О революции» Коперника . Том 1. Спрингер Верлаг. п. 76. ИСБН 0-387-90939-7 . Архивировано из оригинала 16 сентября 2023 г. Получено 22 ноября 2020 г. - через Google Книги .

[Harris1981-12] Jump up to: ^а ^б Харрис, Д.Л. (1981). Приливы и данные о приливах в Соединенных Штатах . Специальный репортаж (Центр прибрежных инженерных исследований (США))). Инженерный корпус армии США , Исследовательский центр прибрежной инженерии. п. 32. Архивировано из оригинала 16 сентября 2023 г. Получено 24 августа 2021 г. - через Google Книги .

[13] "neap²". Оксфордский словарь английского языка (2-е изд.). Издательство Оксфордского университета . 1989. Древнеанглийский (пример, приведенный в 469 году нашей эры: forðganges nip – без возможности продвижения). Датский ниптид, вероятно, произошел от английского. Английский термин «neap-flood» (от которого происходит «neap tide»), по-видимому, стал широко использоваться к 725 году нашей эры.

[14] «Что такое перигейский весенний прилив?» . Национальное управление океанических и атмосферных исследований. 26 февраля 2021 года. Архивировано из оригинала 30 июля 2021 года . Проверено 16 июля 2021 г.

[leprovost-15] Ле Провост, Кристиан (1991). «Генерация приливов и сложных приливов (обзор)». В Паркер, Брюс Б. (ред.). Приливная гидродинамика . Джон Уайли и сыновья . ISBN 978-0-471-51498-5 .

[16] Аккад, Ю. и Пекерис, К.Л. (28 ноября 1978 г.). «Решение приливных уравнений для приливов M ₂ и S ₂ в Мировом океане на основе знания только приливного потенциала». Философские труды Лондонского королевского общества А. 290 (1368): 235–266. Бибкод : 1978RSPTA.290..235A . дои : 10.1098/rsta.1978.0083 . S2CID 119526571 .

[17] «Прогноз приливов» . Новая Зеландия: Национальный институт исследований воды и атмосферы. Архивировано из оригинала 14 октября 2008 г. Проверено 7 ноября 2008 г. Включая анимацию приливов M2, S2 и K1 для Новой Зеландии.

[18] Марчук, Гури И.; Каган, бакалавр наук (6 декабря 2012 г.). Динамика океанских приливов . Спрингер. ISBN 9789400925717 . Архивировано из оригинала 16 сентября 2023 года . Проверено 22 ноября 2020 г. - через Google Книги .

[19] Шуреман, Пол (1971). Руководство по гармоническому анализу и прогнозированию приливов и отливов . Побережье США и геодезическая съемка. п. 204. Архивировано из оригинала 8 августа 2017 г. Проверено 14 января 2018 г.

[20] Птолемей (1940). «2». Тетрабиблос . Том. 1. Перевод Роббинса, Фрэнка Э. Кембриджа, Массачусетс: Издательство Гарвардского университета .

[Wallis-22] Беде (1999). Расчёт времени . Перевод Уоллис, Фейт. Издательство Ливерпульского университета . п. 82. ИСБН 0-85323-693-3 . Архивировано из оригинала 9 апреля 2023 года . Проверено 1 июня 2018 г. - через Google Книги .

[FOOTNOTEBede199983-23] Беде 1999 , стр. 83.

[FOOTNOTEBede199984-24] Jump up to: ^а ^б Беде 1999 , стр. 84.

[FOOTNOTEBede199985-25] Jump up to: ^а ^б Беде 1999 , стр. 85.

[Tolmacheva-26] Jump up to: ^а ^б ^с ^д Толмачева, Марина (2014). Глик, Томас Ф. (ред.). География, Хорография . Рутледж . п. 188. ИСБН 978-1135459321 . {{cite book}}: |work= игнорируется ( помогите )

[27] «Саймон Стевин» (PDF) (pdf) (на голландском языке). Фландрийский морской институт. Архивировано (PDF) из оригинала 5 августа 2014 г. Проверено 1 июня 2014 г.

[28] Пальмерино, Карла Рита; Тийссен, JMMH (31 августа 2004 г.). Рецепция галилеевой науки о движении в Европе семнадцатого века . Springer Science+Business Media . п. 200. ИСБН 978-1-4020-2455-9 . Архивировано из оригинала 12 апреля 2022 года . Проверено 29 ноября 2022 г. - через Google Книги .

[29] Иоганн Кеплер, Astronomia nova ... (1609), с. 5 Introductio in hoc opus (Введение к данной работе). Со страницы 5:

[slc-ch2-31] Jump up to: ^а ^б Лисицын, Е. (1974). "2 "Периодические изменения уровня моря: Астрономические приливы" ". Изменения уровня моря (Серия Elsevier Oceanography) . Том. 8. с. 5.

[32] «Что вызывает приливы?» . США Национальная океаническая служба Национального управления океанических и атмосферных исследований (НОАА) (раздел образования). Архивировано из оригинала 20 августа 2016 г. Проверено 6 сентября 2009 г.

[34] Вар, Дж. (1995). Земные приливы в «Глобальной физике Земли», Справочная полка № 1 Американского геофизического союза . стр. 40–46.

[EulerAiton1996-35] Эйлер, Леонард ; Эйтон, Эрик Дж. (1996). Механические и астрономические наблюдения, относящиеся к физике . Springer Science+Business Media . стр. 19–. ISBN 978-3-7643-1459-0 – через Google Книги .

[Cook-36] Томсон, Томас , изд. (март 1819 г.). «О рассказе капитана Кука о приливах» . Анналы философии . ХIII . Лондон: Болдуин, Крэдок и Джой: 204. Архивировано из оригинала 26 августа 2016 года . Проверено 25 июля 2015 г.

[tidhist-37] Jump up to: ^а ^б Цзошэн, Ю.; Эмери, нокаут и Юи, X. (июль 1989 г.). «Историческое развитие и использование тысячелетних таблиц прогнозирования приливов» . Лимнология и океанография . 34 (5): 953–957. Бибкод : 1989LimOc..34..953Z . дои : 10.4319/lo.1989.34.5.0953 .

[38] Картрайт, Дэвид Э. (1999). Приливы: научная история . Кембридж, Великобритания: Издательство Кембриджского университета . ISBN 9780521621458 .

[39] Кейс, Джеймс (март 2000 г.). «Понимание приливов - от древних верований к современным решениям уравнений Лапласа». СИАМ Новости . 33 (2).

[40] Дудсон, А.Т. (декабрь 1921 г.). «Гармоническое развитие приливно-генерирующего потенциала» . Труды Лондонского королевского общества А. 100 (704): 305–329. Бибкод : 1921RSPSA.100..305D . дои : 10.1098/rspa.1921.0088 .

[41] Казотто С. и Бискани Ф. (апрель 2004 г.). «Полностью аналитический подход к гармоническому развитию приливно-генерирующего потенциала с учетом прецессии, нутации и возмущений, вызванных фигурными и планетарными условиями». Отделение ААН по динамической астрономии . 36 (2): 67. Бибкод : 2004DDA....35.0805C .

[42] Мойер, Т.Д. (2003). Формулировка наблюдаемых и вычисленных значений типов данных Deep Space Network для навигации (PDF) . Связь и навигация в дальнем космосе. Том. 3. Уайли . стр. 126–128. ISBN 0-471-44535-5 . Архивировано из оригинала (PDF) 16 октября 2004 г.

[43] Flussi e reflux [ Приливы и отливы ] (на итальянском языке). Милан: Фельтринелли. 2003. ISBN 88-07-10349-4 .

[44] ван дер Варден, БЛ (1987). «Гелиоцентрическая система в греческой, персидской и индуистской астрономии». Анналы Нью-Йоркской академии наук . 500 (1): 525–545 [527]. Бибкод : 1987NYASA.500..525V . дои : 10.1111/j.1749-6632.1987.tb37224.x . S2CID 222087224 .

[45] Картрайт, Делавэр (1999). «Приливы, научная история» . Эос-транзакции . 80 (36): 11, 18. Бибкод : 1999EOSTr..80..408A . дои : 10.1029/99EO00304 .

[46] «Аборигенная астрономия предсказывает влияние Луны на приливы и отливы до Галилея и Ньютона» (на бразильском португальском языке). 19 июня 2009 г. Проверено 11 декабря 2021 г.

[47] «Машина для предсказания приливов Дудсона-Леже» . Океанографическая лаборатория Праудмана. Архивировано из оригинала 20 марта 2009 г. Проверено 3 октября 2008 г.

[48] Лаббок, JW (1831 г.). «О приливах у берегов Великобритании» . Философский журнал . 9 (53): 333–335. дои : 10.1080/14786443108647618 .

[49] Уэвелл, Уильям (1836). «Исследования о приливах, серия шестая. О результатах обширной системы приливных наблюдений, произведенных на побережьях Европы и Америки в июне 1835 года» . Философские труды Лондонского королевского общества . 126 : 289–341.

[50] Хьюитт, Уильям (1841). «Приливно-отливные наблюдения в Северном море» . Морской журнал : 180–183.

[Cartwright2000-51] Картрайт, Дэвид Эдгар (17 августа 2000 г.). Приливы: научная история . Издательство Кембриджского университета . ISBN 978-0-521-79746-7 . OCLC 1001932580 .

[Kuecher_et_al._1990-52] Кучер, Джеральд Дж.; Вудленд, Бертрам Г.; Бродхерст, Фредерик М. (1 сентября 1990 г.). «Свидетельства отложений в результате отдельных приливов и приливных циклов из сланцев Фрэнсис-Крик (вмещающая порода биоты Мейзон-Крик), Вестфальский период D (Пенсильвания), северо-восточный Иллинойс» . Осадочная геология . 68 (3): 211–221. Бибкод : 1990SedG...68..211K . дои : 10.1016/0037-0738(90)90113-8 . ISSN 0037-0738 .

[Archer_et_al._1995-53] Арчер, Аллен В.; Кучер, Джеральд Дж; Квале, Эрик П. (1995). «Роль асимметрии приливных скоростей в отложении илистых приливных ритмитов (каменноугольный период, Восточный внутренний угольный бассейн, США)» . Журнал SEPM осадочных исследований . 65 : 408–416. doi : 10.1306/d42680d6-2b26-11d7-8648000102c1865d .

[54] Янг, Калифорния (1889 г.). Учебник общей астрономии (PDF) . п. 288. Архивировано (PDF) из оригинала 05 октября 2019 г. Проверено 13 августа 2018 г.

[Science_Mission_Directorate_2000-57] «Межпланетный отлив» . Управление научной миссии . 03.05.2000. Архивировано из оригинала 4 июня 2023 г. Проверено 25 июня 2023 г.

[AMS_Glossary_2020-58] «Равновесный прилив» . Глоссарий АМС . 2020-09-02. Архивировано из оригинала 01 августа 2020 г. Проверено 2 сентября 2020 г.

[59] Томпсон, ЛуЭнн (2006). «Физические процессы в океане» (PDF) . Архивировано (PDF) из оригинала 28 сентября 2020 г. Проверено 27 июня 2020 г.

[Hicks2006-61] Хикс, С.Д. (2006). Понимание приливов (PDF) (Отчет). НОАА . Архивировано (PDF) из оригинала 20 января 2022 г. Проверено 2 сентября 2020 г.

[63] Маккалли, Джеймс Грейг (2006). За Луной: разговорное руководство по здравому смыслу для понимания приливов, World Scientific . Всемирная научная. ISBN 9789814338189 . Архивировано из оригинала 16 сентября 2023 г. Получено 5 января 2022 г. - через Google Книги .

[PBS_LearningMedia_2020-65] «Что учителя физики ошибаются в отношении приливов! - PBS Space Time» . PBS LearningMedia . 17.06.2020. Архивировано из оригинала 21 октября 2020 г. Проверено 27 июня 2020 г.

[Munk1998-66] Мунк, В.; Вунш, К. (1998). «Бездные рецепты II: энергетика смешения приливов и ветров». Глубоководные исследования . Часть I. 45 (12): 1977. Бибкод : 1998DSRI...45.1977M . дои : 10.1016/S0967-0637(98)00070-3 .

[Ray1996-67] Рэй, РД; Инес, Р.Дж.; Чао, Б.Ф. (1996). «Обнаружение приливной диссипации в твердой Земле с помощью спутникового слежения и альтиметрии». Природа . 381 (6583): 595. Бибкод : 1996Natur.381..595R . дои : 10.1038/381595a0 . S2CID 4367240 .

[68] Лекция 2: Роль приливной диссипации и приливные уравнения Лапласа Мирла Хендершотта. Том GFD Proceedings, 2004 г., примечания WHOI Ярона Толедо и Маршалла Уорда.

[noaa7b-70] «карта, показывающая мировое распределение режимов приливов: полусуточных, суточных и смешанных полусуточных» . США Национальное управление океанических и атмосферных исследований (NOAA), Национальная океаническая служба (раздел образования) . Архивировано из оригинала 27 августа 2018 г. Проверено 5 сентября 2009 г.

[71] Турман, Х.В. (1994). Вводная океанография (7-е изд.). Нью-Йорк: Издательство Macmillan . стр. 252–276. ссылка

[72] Росс, Д.А. (1995). Введение в океанографию . Нью-Йорк: ХарперКоллинз . стр. 236–242.

[73] Витце, Александра (5 июля 2020 г.). «Как люди меняют приливы и отливы океанов» . BBC Будущее . Би-би-си . Архивировано из оригинала 6 июля 2020 года . Проверено 8 июля 2020 г.

[74] «Глоссарий метеорологии» . Американское метеорологическое общество . Архивировано из оригинала 08 мая 2021 г. Проверено 2 апреля 2021 г.

[75] Вебстер, Томас (1837). Элементы физики . Напечатано для Скотта, Вебстера и Гири. п. 168 .

[76] "ЧАСТО ЗАДАВАЕМЫЕ ВОПРОСЫ" . Архивировано из оригинала 12 февраля 2012 года . Проверено 23 июня 2007 г.

[BIO2004-77] Jump up to: ^а ^б О'Рейли, CTR; Солвасон, Рон и Соломон, Кристиан (2005). Райан, Дж. (ред.). «Где самые большие приливы в мире». Годовой отчет BIO «Обзор 2004 года» . Вашингтон, округ Колумбия: Биотехнологии. Индийская организация: 44–46.

[FundyWorkshop-78] Jump up to: ^а ^б О'рейли, Чарльз Т.; Солвасон, Рон; Соломон, Кристиан (2005). «Решение крупнейших приливов в мире» (PDF) . В Перси, JA; Эванс, Эй Джей; Уэллс, П.Г.; Ролстон, С.Дж. (ред.). Меняющийся залив Фанди - за 400 лет, Материалы 6-го семинара по заливу Фанди, Корнуоллис, Новая Шотландия, 29 сентября 2004 г. - 2 октября 2004 г. Окружающая среда Канады - Атлантический регион, Периодический отчет №. 23. Дартмут, Северная Каролина и Саквилл, Северная Каролина . Архивировано (PDF) из оригинала 27 августа 2016 г. Проверено 1 апреля 2013 г.

[Pingree_1978-79] Пингри, РД; Мэддок, Л. (1978). «Глубоководные исследования». 25 : 53–63. {{cite journal}}: Для цитирования журнала требуется |journal= ( помощь )

[81] Центр оперативной океанографической продукции и услуг, Национальная океаническая служба, Национальное управление океанических и атмосферных исследований (январь 2000 г.). «Глоссарий приливов и течений» (PDF) . Силвер Спринг, Мэриленд. Архивировано (PDF) из оригинала 28 января 2007 г. Проверено 5 апреля 2007 г. {{cite web}}: CS1 maint: несколько имен: список авторов ( ссылка )

[82] «Гармонические составляющие» . НОАА . Архивировано из оригинала 17 марта 2007 г. Проверено 5 апреля 2007 г.

[83] Общество морских исследований (1958). Зеркало моряка . Архивировано из оригинала 16 сентября 2023 г. Проверено 28 апреля 2009 г. - через Google Книги .

[84] Бос, Арканзас; Гуманао, Г.С.; ван Катвейк, ММ; Мюллер, Б.; Саседа, ММ и Техада, РП (2011). «Онтогенетическое изменение среды обитания, рост популяции и роющее поведение индо-тихоокеанской пляжной звезды Archaster typicus (Echinodermata: Asteroidea)» . Морская биология . 158 (3): 639–648. Бибкод : 2011МарБи.158..639B . дои : 10.1007/s00227-010-1588-0 . ПМЦ 3873073 . ПМИД 24391259 .

[85] Бос, А.Р. и Гуманао, Г.С. (2012). «Лунный цикл определяет наличие коралловых рифовых рыб на рыбных рынках». Журнал биологии рыб . 81 (6): 2074–2079. Бибкод : 2012JFBio..81.2074B . дои : 10.1111/j.1095-8649.2012.03454.x . ПМИД 23130702 .

[86] Нэйлор, Эрнест (4 февраля 2010 г.). «Глава 5: Лунные и полулунные биоритмы». Хронобиология морских организмов . Издательство Кембриджского университета . ISBN 978-1-139-48494-7 . Архивировано из оригинала 16 сентября 2023 г. Проверено 3 января 2022 г. - через Google Книги .

[87] Чжу, Бокай; Даксо, Клиффорд К.; О'Мэлли, Берт В. (01 июля 2018 г.). «Открытие «Musica Universalis» клетки: краткая история биологических 12-часовых ритмов» . Журнал Эндокринного общества . 2 (7): 727–752. дои : 10.1210/js.2018-00113 . ISSN 2472-1972 . ПМК 6025213 . ПМИД 29978151 . Архивировано из оригинала 16 сентября 2023 г. Проверено 03 января 2022 г.

[Descent-88] Дарвин, Чарльз (1871). Происхождение человека и отбор по признаку пола . Лондон: Джон Мюррей.

[rocur-89] Ле Лашер, Эмбер А. (апрель 1924 г.). «Приливные течения в открытом море: подземные приливные течения на легком судне Нантакет Шолс» . Географическое обозрение . 14 (2): 282–286. Бибкод : 1924GeoRv..14..282L . дои : 10.2307/208104 . JSTOR 208104 . Архивировано из оригинала 16 сентября 2023 года . Проверено 4 февраля 2012 г.

[90] «Есть ли на Великих озерах приливы?» . Информационная сеть Великих озер. 1 октября 2000 г. Архивировано из оригинала 30 декабря 2017 г. Проверено 10 февраля 2010 г.

[91] Колдер, Винс. «Приливы на озере Мичиган» . Аргоннская национальная лаборатория. Архивировано из оригинала 15 августа 2019 г. Проверено 14 августа 2019 г.

[92] Данкерсон, Дуэйн. «Луна и приливы» . Астрономия Коротко. Архивировано из оригинала 15 января 2010 г. Проверено 10 февраля 2010 г.

[93] «Есть ли на Великих озерах приливы?» . Национальная океаническая служба . НОАА . Архивировано из оригинала 23 апреля 2016 г. Проверено 26 апреля 2016 г.

[94] Нурми, П.; Валтонен, MJ и Чжэн, JQ (2001). «Периодические изменения потока Облака Оорта и воздействия комет на Землю и Юпитер» . Ежемесячные уведомления Королевского астрономического общества . 327 (4): 1367–1376. Бибкод : 2001MNRAS.327.1367N . дои : 10.1046/j.1365-8711.2001.04854.x .

[95] "прилив". Оксфордский словарь английского языка . Том. XVIII (2-е изд.). Издательство Оксфордского университета . 1989. с. 64.

[1]

[2]

[a]

[3]

[4]

[b]

[6]

[7]

[8]

[9]

[10]

[11]

[12]

[13]

[14]

[15]

[16]

[17]

[c]

[19]

[20]

[21]

[22]

[23]

[24]

[25]

[d]

[27]

[28]

[e]

[29]

[30]

[31]

[32]

[33]

[34]

[35]

[36]

[37]

[38]

[39]

[40]

[41]

[42]

[43]

[44]

[45]

[46]

[47]

[48]

[49]

[f]

[g]

[50]

[51]

[h]

[i]

[j]

[55]

[56]

[57]

[k]

[59]

[60]

[61]

[62]

[63]

[64]

[65]

[66]

[67]

[68]

[л]

[69]

[70]

[71]

[72]

[73]

[74]

[75]

[76]

[77]

[78]

[79]

[80]

[81]

[82]

[83]

[5]

[18]

[26]

[52]

[53]

[54]

[58]

v т и Геофизика
Overview	Outline Geophysicists
Subfields	Geodynamics Geophysical survey Geomagnetism Geomathematics Geophysical fluid dynamics Mineral physics Near-surface geophysics Paleomagnetism Seismology Tectonophysics
Physical phenomena	Chandler wobble Coriolis effect Earth's energy budget Earth's magnetic field Geodynamo Geothermal gradient Gravity of Earth Mantle convection Precession of the equinoxes Seismic wave Tide
Related disciplines	Geodesy
Geophysics portal Category Commons

v т и Физическая океанография
Waves	Airy wave theory Ballantine scale Benjamin–Feir instability Boussinesq approximation Breaking wave Clapotis Cnoidal wave Cross sea Dispersion Edge wave Equatorial waves Fetch Gravity wave Green's law Infragravity wave Internal wave Iribarren number Kelvin wave Kinematic wave Longshore drift Luke's variational principle Mild-slope equation Radiation stress Rogue wave Rossby wave Rossby-gravity waves Sea state Seiche Significant wave height Soliton Stokes boundary layer Stokes drift Stokes wave Swell Trochoidal wave Tsunami megatsunami Undertow Ursell number Wave action Wave base Wave height Wave nonlinearity Wave power Wave radar Wave setup Wave shoaling Wave turbulence Wave–current interaction Waves and shallow water one-dimensional Saint-Venant equations shallow water equations Wind setup Wind wave model
Circulation	Atmospheric circulation Baroclinity Boundary current Coriolis force Coriolis–Stokes force Craik–Leibovich vortex force Downwelling Eddy Ekman layer Ekman spiral Ekman transport El Niño–Southern Oscillation General circulation model Geochemical Ocean Sections Study Geostrophic current Global Ocean Data Analysis Project Gulf Stream Halothermal circulation Humboldt Current Hydrothermal circulation Langmuir circulation Longshore drift Loop Current Modular Ocean Model Ocean current Ocean dynamics Ocean dynamical thermostat Ocean gyre Overflow Princeton ocean model Rip current Subsurface currents Sverdrup balance Thermohaline circulation shutdown Upwelling Wind generated current Whirlpool World Ocean Circulation Experiment
Tides	Amphidromic point Earth tide Head of tide Internal tide Lunitidal interval Perigean spring tide Rip tide Rule of twelfths Slack tide Tidal bore Tidal force Tidal power Tidal race Tidal range Tidal resonance Tide gauge Tideline Theory of tides
Landforms	Abyssal fan Abyssal plain Atoll Bathymetric chart Coastal geography Cold seep Continental margin Continental rise Continental shelf Contourite Guyot Hydrography Knoll Oceanic basin Oceanic plateau Oceanic trench Passive margin Seabed Seamount Submarine canyon Submarine volcano
Plate tectonics	Convergent boundary Divergent boundary Fracture zone Hydrothermal vent Marine geology Mid-ocean ridge Mohorovičić discontinuity Vine–Matthews–Morley hypothesis Oceanic crust Outer trench swell Ridge push Seafloor spreading Slab pull Slab suction Slab window Subduction Transform fault Volcanic arc
Ocean zones	Benthic Deep ocean water Deep sea Littoral Mesopelagic Oceanic Pelagic Photic Surf Swash
Sea level	Deep-ocean Assessment and Reporting of Tsunamis Future sea level Global Sea Level Observing System North West Shelf Operational Oceanographic System Sea-level curve Sea level rise Sea level drop World Geodetic System
Acoustics	Deep scattering layer Hydroacoustics Ocean acoustic tomography Sofar bomb SOFAR channel Underwater acoustics
Satellites	Jason-1 Jason-2 (Ocean Surface Topography Mission) Jason-3
Related	Acidification Argo Benthic lander Color of water DSV Alvin Marginal sea Marine energy Marine pollution Mooring National Oceanographic Data Center Ocean Explorations Observations Reanalysis Ocean surface topography Ocean temperature Ocean thermal energy conversion Oceanography Outline of oceanography Pelagic sediment Sea surface microlayer Sea surface temperature Seawater Science On a Sphere Stratification Thermocline Underwater glider Water column World Ocean Atlas
Oceans portal Category Commons

Базы данных авторитетного контроля
International	FAST
National	France BnF data Germany Israel United States Japan Czech Republic