Индо-арабская система счисления
| Часть серии о |
| Системы счисления |
|---|
| Список систем счисления |
Индо -арабская система счисления (также известная как индо-арабская система счисления , [1] Индуистская система счисления , арабская система счисления ) [2] [примечание 1] — позиционная десятичная система счисления для представления целых чисел ; его расширением для нецелых чисел является десятичная система счисления , которая в настоящее время является наиболее распространенной системой счисления.
Система была изобретена между I и IV веками индийскими математиками . Система была принята в арабской математике к 9 веку. Он стал более широко известен благодаря трудам на арабском языке персидского математика Аль-Хорезми. [3] ( «О расчетах индуистскими цифрами» , ок. 825 г. ) и арабский математик Аль-Кинди ( «Об использовании индуистских цифр» , ок. 830 г. ). Эта система распространилась в средневековой Европе в средние века , особенно после написания Фибоначчи » 13-го века «Liber Abaci ; до появления печатного станка в 15 веке использование этой системы в Европе ограничивалось в основном Северной Италией . [4]
Он основан на десяти глифах, представляющих числа от нуля до девяти, и позволяет представлять любое натуральное число уникальной последовательностью этих глифов. Символы (глифы), используемые для представления системы, в принципе независимы от самой системы. Используемые в действительности символы произошли от цифр Брахми разделились на различные типографские варианты и со времен средневековья .
Эти наборы символов можно разделить на три основных семейства: западные арабские цифры, используемые в Большом Магрибе и Европе ; Восточные арабские цифры, используемые на Ближнем Востоке ; и индийские цифры в различных сценариях, используемых на Индийском субконтиненте .
Происхождение
[ редактировать ]Где-то около 600 г. н. э. начались изменения в написании дат в письменности Индии и Юго-Восточной Азии, происходящей от брахми , переход от аддитивной системы с отдельными цифрами для чисел разных величин к позиционной системе разрядных значений с единым набором чисел. глифы для цифр 1–9 и точка для нуля, постепенно вытесняя аддитивные выражения цифр в течение следующих нескольких столетий. [5]
Когда эта система была принята и распространена средневековыми арабами и персами, они назвали ее аль-хисаб аль-хинди («индийская арифметика»). Эти цифры постепенно были приняты в Европе, начиная примерно с 10 века, вероятно, переданные арабскими купцами; [6] европейские математики Средневековья и Возрождения обычно признавали их индийскими по происхождению, [7] однако несколько влиятельных источников приписали их арабам, и в конечном итоге они стали широко известны в Европе как «арабские цифры». [8] Согласно некоторым источникам, эта система счисления, возможно, произошла от китайских цифр Шан (1200 г. до н. э.), которые также представляли собой десятичную позиционную систему счисления. [9]
Позиционные обозначения
[ редактировать ]Индо-арабская система предназначена для позиционной записи в десятичной системе. В более развитой форме позиционное обозначение также использует десятичный маркер (сначала знак над единицей, но теперь чаще десятичная точка или десятичная запятая, которая отделяет единицы от десятых мест), а также символ « эти цифры повторяются до бесконечности ». В современном использовании этот последний символ обычно представляет собой винкулум (горизонтальную линию, расположенную над повторяющимися цифрами). В этой более развитой форме система счисления может обозначать любое рациональное число, используя всего 13 символов (десять цифр, десятичный маркер, винкулум и добавленный знак минус для обозначения отрицательного числа ).
Хотя числа, написанные этими цифрами, обычно встречаются в тексте, написанном арабским абджадом («алфавитом»), в числах, написанных этими цифрами, старшая цифра также размещается слева, поэтому они читаются слева направо (хотя цифры не всегда произносятся в порядке от большинства). до наименее значимого [10] ). Необходимые изменения в направлении чтения обнаруживаются в тексте, в котором смешаны системы письма слева направо и справа налево.
Символы
[ редактировать ]Для представления чисел в индуистско-арабской системе счисления используются различные наборы символов, большинство из которых произошли от цифр Брахми .
разделились на различные типографские варианты Символы, используемые для представления системы, со времен Средневековья , сгруппированные в три основные группы:
- Широко распространенные западные « арабские цифры », используемые с латинским , кириллическим и греческим алфавитами в таблице , произошли от «западно-арабских цифр», которые были разработаны в Аль-Андалусе и Магрибе (существует два типографских стиля для передачи западных арабских цифр) . , известные как фигуры-подкладки и текстовые фигуры ).
- «Арабско-индийские» или « восточно-арабские цифры », используемые с арабским письмом, возникли в основном на территории современного Ирака . [ нужна ссылка ] Вариант восточно-арабских цифр используется в персидском и урду.
- Индийские цифры , используемые в письменах семьи Брахмов в Индии и Юго-Восточной Азии. Каждый из примерно дюжины основных шрифтов Индии имеет свои собственные цифровые глифы (как можно заметить, просматривая таблицы символов Юникода).
Сравнение глифов
[ редактировать ]История
[ редактировать ]Предшественники
[ редактировать ]Цифры Шан
[ редактировать ]
Числа китайской династии Шан, датируемые 14 веком до нашей эры, предшествуют индийским цифрам Брахми более чем на 1000 лет и демонстрируют существенное сходство с цифрами Брахми. Подобно современным арабским цифрам, система счисления династии Шан также была десятичной и позиционной . [11] [12] [13]
Цифры Брахми
[ редактировать ]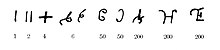
Цифры Брахми , лежащие в основе системы, появились еще до нашей эры . Они заменили более ранние цифры Харости , использовавшиеся с IV века до нашей эры. Цифры Брахми и Кхарости использовались рядом друг с другом в период Империи Маурьев в III веке до нашей эры , оба они появились в указах Ашоки . [14]
В буддийских надписях примерно 300 г. до н. э. используются символы, которые стали цифрами 1, 4 и 6. Столетие спустя было зафиксировано использование ими символов, которые стали цифрами 2, 4, 6, 7 и 9. Эти цифры Брахми являются прародителями индуистско-арабских символов от 1 до 9, но они не использовались как позиционная система с нулем , а для каждой из десятков (10, 20, 30 и т. д.) существовали отдельные цифры. .
Фактическая система счисления, включая позиционное обозначение и использование нуля, в принципе не зависит от используемых глифов и значительно моложе, чем цифры Брахми.
Разработка
[ редактировать ]использована топоместная система В рукописи Бахшали ; самые ранние листья датированы радиоуглеродом периодом 224–383 гг. н.э. [15] Развитие позиционной десятичной системы берет свое начало в индийской математике в период Гуптов . Около 500 г. астроном Арьябхата использует слово кха («пустота») для обозначения «нуля» в табличном расположении цифр. VII века Брахмаспута Сиддханта содержит сравнительно продвинутое понимание математической роли нуля . Санскритский перевод утерянного пракритского джайнского космологического текста Локавибхаги V века.может сохранить ранний пример позиционного использования нуля. [16]
Первая датированная и неоспоримая надпись, показывающая использование символа нуля, появляется на каменной надписи, найденной в храме Чатурбхуджа в Гвалиоре в Индии и датированной 876 годом. [17]
Средневековый исламский мир
[ редактировать ]Эти индийские разработки были использованы в исламской математике в 8 веке, как записано в аль-Кифти » «Хронологии ученых (начало 13 века). [18]
X века В исламской математике система была расширена за счет включения дробей , как записано в трактате Аббасидского халифата математика Абуль-Хасана аль-Уклидиси , который первым описал позиционные десятичные дроби. [19] По мнению Дж. Л. Бреггрена, мусульмане были первыми, кто стал представлять числа так, как это делаем мы, поскольку именно они изначально расширили эту систему счисления для представления частей единицы десятичными дробями, чего индуисты не достигли. Таким образом, мы вполне уместно называем эту систему «индуистско-арабской». [20] [21]
Система счисления стала известна как персидскому математику Хорезми , написавшему книгу «О вычислении индуистскими цифрами» примерно в 825 году, так и арабскому математику Аль-Кинди , написавшему книгу « Об использовании индуистских цифр» ( كتاب في استعمال العداد الهندي [ kitāb fī isti'māl al-'adad al-hindī ]) около 830 года. Персидский учёный Кушьяр Гилани, написавший «Китаб фи усул хисаб аль-хинд» ( «Принципы индуистского исчисления »), является одним из старейших сохранившихся рукописей, использующих индуистские цифры. [22] Эти книги в первую очередь ответственны за распространение индуистской системы счисления во всем исламском мире и, в конечном итоге, в Европе.
Усыновление в Европе
[ редактировать ]
В христианской Европе первое упоминание и изображение индуистско-арабских цифр (от одного до девяти, без нуля) находится в Codex Vigilanus (также известном как Albeldensis ), иллюстрированном сборнике различных исторических документов вестготского периода в Испании , написанном в 976 год тремя монахами Риоханского монастыря Сан-Мартин-де-Альбельда .Между 967 и 969 годами Герберт Орийакский открыл и изучал арабскую науку в каталонских аббатствах. Позже он получил в этих местах книгу De multiplicatione et Divisione ( «Об умножении и делении »). Став Папой Сильвестром II в 999 году, он представил новую модель счетов , так называемые счеты Герберта , приняв жетоны, представляющие индуистско-арабские цифры от одного до девяти.
Леонардо Фибоначчи принес эту систему в Европу. Его книга Liber Abaci представила Modus Indorum (метод индейцев), сегодня известный как индуистско-арабская система счисления или позиционная запись с основанием 10, использование нуля и десятичной системы счисления в латинском мире. Европейцы стали называть эту систему счисления «арабской». Оно использовалось в европейской математике с 12 века и вошло в обиход с 15 века для замены римских цифр . [23] [24]
Знакомая форма западно-арабских символов, используемых сейчас в латинском алфавите (0, 1, 2, 3, 4, 5, 6, 7, 8, 9), возникла в конце 15 — начале 16 веков, когда они начал раннюю верстку .Мусульманские учёные использовали вавилонскую систему счисления , а купцы использовали цифры Абджад , систему, аналогичную греческой системе счисления и еврейской системе счисления . Точно так же введение системы Фибоначчи в Европу было ограничено учеными кругами.Заслуга в первом широко распространенном понимании и использовании десятичной позиционной записи среди населения в целом принадлежит Адаму Рису , автору немецкого Возрождения , чья книга 1522 года «Rechenung auff der linihen und feder» («Расчет по линиям и с помощью пера») была целью у учеников предпринимателей и ремесленников.
Грегор Райш , «Мадам Арифматика» , 1508 г.![Таблица вычислений [de], используемая для арифметических вычислений с использованием римских цифр.](//upload.wikimedia.org/wikipedia/commons/thumb/e/e0/Rechentisch.png/120px-Rechentisch.png)
Таблица вычислений , используемая для арифметических вычислений с использованием римских цифр.
Адам Райс , расчет по линиям и перьям , 1522 год.
Две книги по арифметике, опубликованные в 1514 году: Кёбель (слева) с использованием таблицы вычислений и Бёшентейн с использованием цифр.
Адам Райс , расчет по линиям и перьям (2-е изд.), 1525 г.
Роберт Рекорд , Земля искусств , 1543 г.
Питер Апиан , Торговый вексель , 1527 г.
Адам Райс , расчет по линиям и перьям (2-е изд.), 1525 г.
![Таблица вычислений [de], используемая для арифметических вычислений с использованием римских цифр.](http://upload.wikimedia.org/wikipedia/commons/thumb/e/e0/Rechentisch.png/120px-Rechentisch.png)
Усыновление в Восточной Азии
[ редактировать ]В 690 году нашей эры императрица Ву ввела в обращение зэтианские иероглифы , одним из которых был «〇». Сейчас это слово используется как синоним числа ноль.
В Китае китайские Гаутама Сиддха ввёл индуистские цифры с нулем в 718 году, но математики не сочли их полезными, так как у них уже были десятичные позиционные счётные палочки . [25] [26]
В китайских цифрах кружок (〇) используется для записи нуля в сучжоуских цифрах . Многие историки считают, что он был импортирован из индийских цифр Гаутамой Сиддхой в 718 году, но некоторые китайские ученые полагают, что он был создан из китайского заполнителя текстового пространства «□». [25]
Китайцы и японцы окончательно переняли индуистско-арабские цифры в 19 веке, отказавшись от счетных стержней.
Распространение западноарабского варианта
[ редактировать ]«Западно-арабские» цифры, которые широко использовались в Европе со времен барокко , вторично нашли применение во всем мире вместе с латинским алфавитом и даже значительно превысили современное распространение латинского алфавита , вторгаясь в системы письма в регионах, где другие использовались варианты индуистско-арабских цифр, а также в сочетании с китайским и японским письмом (см. Китайские цифры , Японские цифры ).
См. также
[ редактировать ]Примечания
[ редактировать ]- ↑ « Хинду» — персидское название слова «индейец» в 10 веке, когда арабы приняли систему счисления. Использование слова « индуистский » для обозначения религии возникло позднее.
- ^ 6 — это 륙 в Северной Корее.
Ссылки
[ редактировать ]- ^ Аудун Холм , Геометрия: наше культурное наследие , 2000 г.
- ^ Уильям Даррах Хэлси, Эмануэль Фридман (1983). Энциклопедия Кольера с библиографией и указателем .
Когда Аравийская империя расширялась и были установлены контакты с Индией, арабы переняли индуистскую систему счисления и ранние алгоритмы.
- ^ Брезина, Корона (2006), Аль-Хорезми: изобретатель алгебры , The Rosen Publishing Group, стр. 39–40, ISBN 978-1-4042-0513-0
- ^ Данна, Рафаэле (13 января 2021 г.). «Выяснение: распространение индийско-арабских цифр в европейской традиции практической математики (13–16 вв.)» . Нунций . 36 (1): 5–48. дои : 10.1163/18253911-bja10004 . ISSN 0394-7394 .
- ^ Крисомалис 2010 , стр. 194–197.
- ^ Смит и Карпински 1911 , гл. 7, стр. 99–127 .
- ^ Смит и Карпински 1911 , с. 2 .
- ↑ Особого внимания заслуживает Иоганна де Сакробоско XIII века «Алгоризм» , который пользовался чрезвычайной популярностью и влиянием. См. Смит и Карпински, 1911 , стр. 134–135 .
- ^ Свец, Фрэнк (1984). «Эволюция математики в Древнем Китае» . В Кэмпбелле, Дуглас М.; Хиггинс, Джон К. (ред.). Математика: Люди, Проблемы, Результаты . Тейлор и Фрэнсис. ISBN 978-0-534-02879-4 . Лам, Лэй Йонг (1988). «Китайский генезис: переписывание истории нашей системы счисления». Архив истории точных наук . 38 (2): 101–108. дои : 10.1007/BF00348453 . JSTOR 41133830 . Лам, Лэй Йонг (2008). «Счет: китайские счетные палочки» . В Селин, Селаин (ред.). Энциклопедия истории науки, техники и медицины в незападных культурах . Спрингер. ISBN 978-1-4020-4559-2 .
- ^ В немецком языке число вроде 21 произносится как «один двадцать», как если бы оно читалось справа налево. В библейском иврите это иногда делается даже с большими числами, как в Есфири 1:1, где буквально говорится: «Агасфер, который царствовал от Индии до Эфиопии, над семью двадцатью и сотней провинциями».
- ^ Jump up to: Перейти обратно: а б Кэмпбелл, Дуглас М.; Хиггинс, Джон К. (1984). Математика: Люди, Проблемы, Результаты . Тейлор и Фрэнсис. ISBN 978-0-534-02879-4 .
- ^ Jump up to: Перейти обратно: а б The Shorter Science & Civilization in China Vol 2, Сокращение Колином Ронаном оригинального текста Джозефа Нидхэма, таблица 20, стр. 6, Издательство Кембриджского университета ISBN 0-521-23582-0
- ^ Лей-Йонг, Лам (1988). «Китайский Бытие: переписывание истории нашей системы счисления» . Архив истории точных наук . 38 (2): 101–108. ISSN 0003-9519 .
- ^ Флегг 1984 , с. 67 и след. .
- ^ Пирс, Ян (май 2002 г.). «Рукопись Бахшали» . Архив MacTutor «История математики» . Проверено 24 июля 2007 г.
- ^ Ифра, Г. Универсальная история чисел: от предыстории до изобретения компьютера. John Wiley and Sons Inc., 2000. Перевод с французского Дэвида Беллоса, Э.Ф. Хардинга, Софи Вуд и Яна Монка.
- ^ Билл Кассельман (февраль 2007 г.). «Все зря» . Колонка функций . АМС.
- ^ аль-Кифти Хронология ученых (начало 13 века):
- в 776 году предстал человек из Индии, ... перед халифом аль-Мансуром хорошо владевший методом сиддханты расчета, связанного с движением небесных светил, и владевший способами расчета уравнений, основанных на полухорде [по сути синус], рассчитанный в полградуса... Аль-Мансур приказал перевести эту книгу на арабский язык и написать на основе перевода работу, чтобы дать арабам прочную основу для расчета движений планеты...
- ^ Берггрен, Дж. Леннарт (2007). «Математика в средневековом исламе». В Каце, Виктор Дж. (ред.). Математика Египта, Месопотамии, Китая, Индии и ислама: справочник . Издательство Принстонского университета. п. 530. ИСБН 978-0-691-11485-9 .
- ^ Берггрен, Дж. Л. (18 января 2017 г.). Эпизоды математики средневекового ислама . Спрингер. ISBN 978-1-4939-3780-6 .
- ^ Берггрен, Дж. Леннарт (2007). «Математика в средневековом исламе». Математика Египта, Месопотамии, Китая, Индии и ислама: справочник . Издательство Принстонского университета. п. 518. ИСБН 978-0-691-11485-9 .
- ^ Мартин Леви и Марвин Петрук, Принципы индуистского исчисления, перевод Кушьяра ибн Лаббана Китаба фи усул хисаб аль-хинд, стр. 3, Университет Висконсина, 1965 г.
- ^ «Числа Фибоначчи» . www.halexandria.org .
- ^ H Леонардо Пизано: «Вклад в теорию чисел» . Британская энциклопедия Online, 2006. стр. 3. Проверено 18 сентября 2006 г.
- ^ Jump up to: Перейти обратно: а б Цянь, Баосун (1964), Чжунго Шусюэ Ши (История китайской математики) , Пекин: Кексюэ Чубанше
- ^ Ван, Цинсян (1999), Санги о коэта отоко (Человек, который превзошел счетные палочки) , Токио: Тойо Сётэн, ISBN 4-88595-226-3
Библиография
[ редактировать ]- Хрисомалис, Стивен (2010). Числовая запись: сравнительная история . Издательство Кембриджского университета. ISBN 978-0-521-87818-0 .
- Флегг, Грэм (1984). Числа: их история и значение . Пингвин. ISBN 978-0-14-022564-8 .
- О'Коннор, Джон Дж.; Робертсон, Эдмунд Ф. (2001). «Арабская система счисления» . MacTutor Архив истории математики . Университет Сент-Эндрюс .
- О'Коннор, Джон Дж.; Робертсон, Эдмунд Ф. (2000). «Индийские цифры» . MacTutor Архив истории математики . Университет Сент-Эндрюс .
- Смит, Дэвид Юджин ; Карпинский, Луи Шарль (1911). Индо-арабские цифры . Бостон: Джинн.
Дальнейшее чтение
[ редактировать ]- Меннингер, Карл В. (1969). Числовые слова и числовые символы: культурная история чисел . МТИ Пресс. ISBN 0-262-13040-8 .
- О генеалогии современных цифр Эдварда Клайва Бэйли
