Индо-арабская система счисления
| Часть серии о |
| Системы счисления |
|---|
| Список систем счисления |
Индо -арабская система счисления (также известная как индо-арабская система счисления , [1] Индуистская система счисления , арабская система счисления ) [2] [примечание 1] — позиционная десятичная система счисления для представления целых чисел ; его расширением для нецелых чисел является десятичная система счисления , которая в настоящее время является наиболее распространенной системой счисления.
Система была изобретена между I и IV веками индийскими математиками . Система была принята в арабской математике к 9 веку. Он стал более широко известен благодаря трудам на арабском языке персидского математика Аль-Хорезми. [3] ( «О расчетах индуистскими цифрами» , ок. 825 г. ) и арабский математик Аль-Кинди ( «Об использовании индуистских цифр» , ок. 830 г. ). Эта система распространилась в средневековой Европе в средние века , особенно после написания Фибоначчи » 13-го века «Liber Abaci ; до появления печатного станка в 15 веке использование этой системы в Европе ограничивалось в основном Северной Италией . [4]
Он основан на десяти глифах, представляющих числа от нуля до девяти, и позволяет представлять любое натуральное число уникальной последовательностью этих глифов. Символы (глифы), используемые для представления системы, в принципе независимы от самой системы. Используемые в действительности символы произошли от цифр Брахми разделились на различные типографские варианты и со времен средневековья .
Эти наборы символов можно разделить на три основных семейства: западные арабские цифры, используемые в Большом Магрибе и Европе ; Восточные арабские цифры, используемые на Ближнем Востоке ; и индийские цифры в различных сценариях, используемых на Индийском субконтиненте .
Происхождение
[ редактировать ]Где-то около 600 г. н. э. начались изменения в написании дат в письменности Индии и Юго-Восточной Азии, происходящей от брахми , переход от аддитивной системы с отдельными цифрами для чисел разной величины к позиционной системе разрядов с единым набором чисел. глифы для цифр 1–9 и точка для нуля, постепенно вытесняя аддитивные выражения цифр в течение следующих нескольких столетий. [5]
Когда эта система была принята и распространена средневековыми арабами и персами, они назвали ее аль-хисаб аль-хинди («индийская арифметика»). Эти цифры постепенно были приняты в Европе, начиная примерно с 10 века, вероятно, переданные арабскими купцами; [6] европейские математики Средневековья и Возрождения обычно признавали их индийскими по происхождению, [7] однако несколько влиятельных источников приписали их арабам, и в конечном итоге они стали широко известны в Европе как «арабские цифры». [8] Согласно некоторым источникам, эта система счисления, возможно, произошла от китайских цифр Шан (1300 г. до н. э.), которые также представляли собой десятичную позиционную систему счисления. [9]
Позиционные обозначения
[ редактировать ]Индо-арабская система предназначена для позиционной записи в десятичной системе. В более развитой форме позиционное обозначение также использует десятичный маркер (сначала знак над единицей, но теперь чаще десятичная точка или десятичная запятая, которая отделяет единицы от десятых мест), а также символ « эти цифры повторяются до бесконечности ». В современном использовании этот последний символ обычно представляет собой винкулум (горизонтальную линию, расположенную над повторяющимися цифрами). В этой более развитой форме система счисления может обозначать любое рациональное число, используя всего 13 символов (десять цифр, десятичный маркер, винкулум и добавленный знак минус для обозначения отрицательного числа ).
Хотя числа, написанные этими цифрами, обычно встречаются в тексте, написанном арабским абджадом («алфавитом»), в числах, написанных этими цифрами, старшая цифра также размещается слева, поэтому они читаются слева направо (хотя цифры не всегда произносятся в порядке от большинства). до наименее значимого [10] ). Необходимые изменения в направлении чтения обнаруживаются в тексте, в котором смешаны системы письма слева направо и справа налево.
Символы
[ редактировать ]Для представления чисел в индуистско-арабской системе счисления используются различные наборы символов, большинство из которых произошли от цифр Брахми .
разделились на различные типографские варианты Символы, используемые для представления системы, со времен Средневековья , сгруппированные в три основные группы:
- Широко распространенные западные « арабские цифры », используемые с латинским , кириллическим и греческим алфавитами в таблице , произошли от «западно-арабских цифр», которые были разработаны в Аль-Андалусе и Магрибе (существует два типографских стиля для передачи западных арабских цифр) . , известные как фигуры-подкладки и текстовые фигуры ).
- «Арабско-индийские» или « восточно-арабские цифры », используемые с арабским письмом, возникли в основном на территории современного Ирака . [ нужна ссылка ] Вариант восточно-арабских цифр используется в персидском и урду.
- Индийские цифры , используемые в письменах семьи Брахмов в Индии и Юго-Восточной Азии. Каждый из примерно дюжины основных шрифтов Индии имеет свои собственные цифровые глифы (как можно заметить, просматривая таблицы символов Юникода).
Сравнение глифов
[ редактировать ]История
[ редактировать ]Предшественники
[ редактировать ]Цифры Шан
[ редактировать ]
Числа китайской династии Шан, датируемые 14 веком до нашей эры, предшествуют индийским цифрам Брахми более чем на 1000 лет и демонстрируют существенное сходство с цифрами Брахми. Подобно современным индуистско-арабским цифрам, система счисления династии Шан также была десятичной и позиционной . [11] [12] [13] Ноль был представлен пустым пространством. [14] [15] Это концептуальное сходство побудило некоторых ученых предположить возможность китайского влияния на индуистско-арабские цифры. [16] [17]
Цифры Брахми
[ редактировать ]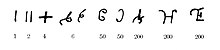
Цифры Брахми , лежащие в основе системы, появились еще до нашей эры . Они заменили более ранние цифры Харости , использовавшиеся с IV века до нашей эры. Цифры Брахми и Кхарости использовались рядом друг с другом в период Империи Маурьев в III веке до нашей эры , и оба они появились в указах Ашоки . [18]
В буддийских надписях примерно 300 г. до н. э. используются символы, которые стали цифрами 1, 4 и 6. Столетие спустя было зафиксировано использование ими символов, которые стали цифрами 2, 4, 6, 7 и 9. Эти цифры Брахми являются прародителями индуистско-арабских символов от 1 до 9, но они не использовались как позиционная система с нулем , а для каждой из десятков (10, 20, 30 и т. д.) существовали отдельные цифры. .
Разработка
[ редактировать ]использована топоместная система В рукописи Бахшали ; самые ранние листья датированы радиоуглеродом периодом 224–383 гг. н.э. [19] Развитие позиционной десятичной системы берет свое начало в индийской математике в период Гуптов . Около 500 г. астроном Арьябхата использует слово кха («пустота») для обозначения «нуля» в табличном расположении цифр. VII века Брахмаспута Сиддханта содержит сравнительно продвинутое понимание математической роли нуля . Санскритский перевод утерянного пракритского джайнского космологического текста Локавибхаги V века.может сохранить ранний пример позиционного использования нуля. [20]
Первая датированная и неоспоримая надпись, показывающая использование символа нуля, появляется на каменной надписи, найденной в храме Чатурбхуджа в Гвалиоре в Индии и датированной 876 годом. [21]
Средневековый исламский мир
[ редактировать ]Эти индийские разработки были использованы в исламской математике в 8 веке, как записано в аль-Кифти » «Хронологии ученых (начало 13 века). [22]
В исламской математике 10-го века система была расширена за счет включения дробей , как записано в трактате Аббасидского халифата математика Абуль-Хасана аль-Уклидиси , который первым описал позиционные десятичные дроби. [23] Арабы были первыми, кто стал представлять числа так, как мы это делаем сейчас, поскольку изначально они расширили индуистскую систему счисления, включив в нее части меньше 1, используя десятичные дроби. Таким образом, мы называем эту систему «индуистско-арабской». [24] [25]
Система счисления стала известна как персидскому математику Хорезми , написавшему книгу «О вычислении индуистскими цифрами» примерно в 825 году, так и арабскому математику Аль-Кинди , написавшему книгу « Об использовании индуистских цифр» ( كتاب في استعمال العداد الهندي [ kitāb fī isti'māl al-'adad al-hindī ]) около 830 года. Персидский учёный Кушьяр Гилани написал «Китаб фи усул хисаб аль-хинд» ( «Принципы индуистского исчисления ») , одну из старейших сохранившихся рукописей с использованием Индуистские цифры. [26] Эти книги в основном ответственны за распространение индуистской системы счисления во всем исламском мире и, в конечном итоге, в Европе.
Усыновление в Европе
[ редактировать ]
В христианской Европе первое упоминание и изображение индуистско-арабских цифр (от одного до девяти, без нуля) находится в Codex Vigilanus (также известном как Albeldensis ), иллюстрированном сборнике различных исторических документов вестготского периода в Испании , написанном в 976 год тремя монахами Риоханского монастыря Сан-Мартин-де-Альбельда .Между 967 и 969 годами Герберт Орийакский открыл и изучал арабскую науку в каталонских аббатствах. Позже он получил в этих местах книгу De multiplicatione et Divisione ( «Об умножении и делении »). Став Папой Сильвестром II в 999 году, он представил новую модель счетов , так называемые счеты Герберта , приняв жетоны, представляющие индуистско-арабские цифры от одного до девяти.
Леонардо Фибоначчи принес эту систему в Европу. Его книга Liber Abaci представила Modus Indorum (метод индейцев), сегодня известный как индуистско-арабская система счисления или позиционная запись с основанием 10, использование нуля и десятичной системы счисления в латинском мире. Европейцы стали называть эту систему счисления «арабской». Оно использовалось в европейской математике с 12 века и вошло в обиход с 15 века для замены римских цифр . [27] [28]
Знакомая форма западно-арабских символов, используемых сейчас в латинском алфавите (0, 1, 2, 3, 4, 5, 6, 7, 8, 9), возникла в конце 15 — начале 16 веков, когда они начал раннюю верстку .Мусульманские учёные использовали вавилонскую систему счисления , а купцы использовали цифры Абджад , систему, аналогичную греческой системе счисления и еврейской системе счисления . Точно так же введение системы Фибоначчи в Европу было ограничено учеными кругами.Заслуга в первом широко распространенном понимании и использовании десятичной позиционной записи среди населения в целом принадлежит Адаму Рису , автору немецкого Возрождения , чья книга 1522 года «Rechenung auff der linihen und feder» («Расчет по линиям и с помощью пера») была целью у учеников предпринимателей и ремесленников.
Грегор Райш , «Мадам Арифматика» , 1508 г.![Таблица вычислений [de], используемая для арифметических вычислений с использованием римских цифр.](//upload.wikimedia.org/wikipedia/commons/thumb/e/e0/Rechentisch.png/120px-Rechentisch.png)
Таблица вычислений , используемая для арифметических вычислений с использованием римских цифр.
Адам Райс , расчет по линиям и перьям , 1522 год.
Две книги по арифметике, опубликованные в 1514 году: Кёбель (слева) с использованием таблицы вычислений и Бёшентейн с использованием цифр.
Адам Райс , расчет по линиям и перьям (2-е изд.), 1525 г.
Робер Рекорд , Земля искусств , 1543 г.
Питер Апиан , Торговый вексель , 1527 г.
Адам Райс , расчет по линиям и перьям (2-е изд.), 1525 г.
![Таблица вычислений [de], используемая для арифметических вычислений с использованием римских цифр.](http://upload.wikimedia.org/wikipedia/commons/thumb/e/e0/Rechentisch.png/120px-Rechentisch.png)
Усыновление в Восточной Азии
[ редактировать ]В 690 году нашей эры императрица Ву ввела в обращение зэтианские иероглифы , одним из которых был «〇». Сейчас это слово используется как синоним числа ноль.
В Китае китайские Гаутама Сиддха ввёл индуистские цифры с нулем в 718 году, но математики не сочли их полезными, так как у них уже были десятичные позиционные счётные палочки . [29] [30]
В китайских цифрах кружок (〇) используется для записи нуля в сучжоуских цифрах . Многие историки полагают, что он был импортирован из индийских цифр Гаутамой Сиддхой в 718 году, но некоторые китайские ученые полагают, что он был создан из китайского заполнителя текстового пространства «□». [29]
Китайцы и японцы окончательно переняли индуистско-арабские цифры в 19 веке, отказавшись от счетных стержней.
Распространение западноарабского варианта
[ редактировать ]«Западно-арабские» цифры, которые широко использовались в Европе со времен барокко , вторично нашли применение во всем мире вместе с латинским алфавитом и даже значительно превысили современное распространение латинского алфавита , вторгаясь в системы письма в регионах, где другие использовались варианты индуистско-арабских цифр, а также в сочетании с китайским и японским письмом (см. Китайские цифры , Японские цифры ).
См. также
[ редактировать ]Примечания
[ редактировать ]- ↑ « Хинду» — персидское название слова «индейец» в 10 веке, когда арабы приняли систему счисления. Использование слова « индуистский » для обозначения религии возникло позднее.
- ^ 6 — это 륙 в Северной Корее.
Ссылки
[ редактировать ]- ^ Аудун Холм , Геометрия: наше культурное наследие , 2000 г.
- ^ Уильям Даррах Хэлси, Эмануэль Фридман (1983). Энциклопедия Кольера с библиографией и указателем .
Когда Аравийская империя расширялась и были установлены контакты с Индией, арабы переняли индуистскую систему счисления и ранние алгоритмы.
- ^ Брезина, Корона (2006), Аль-Хорезми: изобретатель алгебры , The Rosen Publishing Group, стр. 39–40, ISBN 978-1-4042-0513-0
- ^ Данна, Рафаэле (13 января 2021 г.). «Выяснение: распространение индийско-арабских цифр в европейской традиции практической математики (13–16 вв.)» . Нунций . 36 (1): 5–48. дои : 10.1163/18253911-bja10004 . ISSN 0394-7394 .
- ^ Крисомалис 2010 , стр. 194–197.
- ^ Смит и Карпински 1911 , гл. 7, стр. 99–127 .
- ^ Смит и Карпински 1911 , с. 2 .
- ↑ Особого внимания заслуживает Иоганна де Сакробоско XIII века «Алгоризм» , который пользовался чрезвычайной популярностью и влиянием. См. Смит и Карпински, 1911 , стр. 134–135 .
- ^ Свец, Фрэнк (1984). «Эволюция математики в Древнем Китае» . В Кэмпбелле, Дуглас М.; Хиггинс, Джон К. (ред.). Математика: Люди, Проблемы, Результаты . Тейлор и Фрэнсис. ISBN 978-0-534-02879-4 . Лам, Лэй Йонг (1988). «Китайский генезис: переписывание истории нашей системы счисления». Архив истории точных наук . 38 (2): 101–108. дои : 10.1007/BF00348453 . JSTOR 41133830 . Лам, Лэй Йонг (2008). «Счет: китайские счетные палочки» . В Селин, Селаин (ред.). Энциклопедия истории науки, техники и медицины в незападных культурах . Спрингер. ISBN 978-1-4020-4559-2 .
- ^ В немецком языке число вроде 21 произносится как «один двадцать», как если бы оно читалось справа налево. В библейском иврите это иногда делается даже с большими числами, как в Есфири 1:1, где буквально говорится: «Агасфер, который царствовал от Индии до Эфиопии, над семью двадцатью и сотней провинциями».
- ^ Перейти обратно: а б Кэмпбелл, Дуглас М.; Хиггинс, Джон К. (1984). Математика: Люди, Проблемы, Результаты . Тейлор и Фрэнсис. ISBN 978-0-534-02879-4 .
- ^ Перейти обратно: а б Краткий обзор «Наука и цивилизация в Китае», том 2, сокращение Колином Ронаном оригинального текста Джозефа Нидхэма, таблица 20, стр. 6, Издательство Кембриджского университета ISBN 0-521-23582-0
- ^ Лей-Йонг, Лам (1988). «Китайский Бытие: переписывание истории нашей системы счисления» . Архив истории точных наук . 38 (2): 101–108. дои : 10.1007/BF00348453 . ISSN 0003-9519 . JSTOR 41133830 .
- ^ Кац, Виктор Дж.; Михаловиз, Карен Ди (2 марта 2020 г.). Исторические модули для преподавания и изучения математики . Американское математическое соц. ISBN 978-1-4704-5711-2 .
- ^ Асвал, Динеш К.; Ядав, Санджай; Такацудзи, Тосиюки; Рачаконда, Прем; Кумар, Хариш (23 августа 2023 г.). Справочник по метрологии и приложениям . Весенняя природа. ISBN 978-981-99-2074-7 .
- ^ Йонг, Лам Лэй (1996). «Развитие индийско-арабской и традиционной китайской арифметики» . Китайская наука (13): 35–54. ISSN 0361-9001 . JSTOR 43290379 .
- ^ Ву, Хунси (2011). Понимание чисел в математике начальной школы . Американское математическое соц. ISBN 978-0-8218-5260-6 .
- ^ Флегг 1984 , с. 67 и след. .
- ^ Пирс, Ян (май 2002 г.). «Рукопись Бахшали» . Архив MacTutor «История математики» . Проверено 24 июля 2007 г.
- ^ Ифра, Г. Универсальная история чисел: от предыстории до изобретения компьютера. John Wiley and Sons Inc., 2000. Перевод с французского Дэвида Беллоса, Э. Ф. Хардинга, Софи Вуд и Яна Монка.
- ^ Билл Кассельман (февраль 2007 г.). «Все зря» . Колонка функций . АМС.
- ^ аль-Кифти Хронология ученых (начало 13 века):
- в 776 году предстал человек из Индии, ... перед халифом аль-Мансуром хорошо владевший методом сиддханты расчета, связанного с движением небесных тел, и владевший способами расчета уравнений, основанных на полухорде [по сути синус], рассчитанный в полградуса... Аль-Мансур приказал перевести эту книгу на арабский язык и написать на основе перевода работу, чтобы дать арабам прочную основу для расчета движений планеты...
- ^ Берггрен, Дж. Леннарт (2007). «Математика в средневековом исламе». В Каце, Виктор Дж. (ред.). Математика Египта, Месопотамии, Китая, Индии и ислама: справочник . Издательство Принстонского университета. п. 530. ИСБН 978-0-691-11485-9 .
- ^ Берггрен, Дж. Л. (18 января 2017 г.). Эпизоды математики средневекового ислама . Спрингер. ISBN 978-1-4939-3780-6 .
- ^ Берггрен, Дж. Леннарт (2007). «Математика в средневековом исламе». Математика Египта, Месопотамии, Китая, Индии и ислама: справочник . Издательство Принстонского университета. п. 518. ИСБН 978-0-691-11485-9 .
- ^ Ибн Лаббан, Кушьяр (1965). Китаб фи усул хисаб аль-хинд [ Принципы индуистского исчисления ]. Перевод Леви, Мартин ; Петрук, Марвин. Мэдисон: Издательство Университета Висконсина. п. 3. LCCN 65012106 . ОЛ 5941486М .
- ^ «Числа Фибоначчи» . www.halexandria.org .
- ^ H Леонардо Пизано: «Вклад в теорию чисел» . Британская энциклопедия Online, 2006. стр. 3. Проверено 18 сентября 2006 г.
- ^ Перейти обратно: а б Цянь, Баосун (1964), Чжунго Шусюэ Ши (История китайской математики) , Пекин: Кексюэ Чубанше
- ^ Ван, Цинсян (1999), Sangi o koeta otoko (Человек, который превзошел счетные палочки) , Токио: Toyō Shoten, ISBN 4-88595-226-3
Библиография
[ редактировать ]- Хрисомалис, Стивен (2010). Числовая запись: сравнительная история . Издательство Кембриджского университета. ISBN 978-0-521-87818-0 .
- Флегг, Грэм (1984). Числа: их история и значение . Пингвин. ISBN 978-0-14-022564-8 .
- О'Коннор, Джон Дж.; Робертсон, Эдмунд Ф. (2001). «Арабская система счисления» . MacTutor Архив истории математики . Университет Сент-Эндрюс .
- О'Коннор, Джон Дж.; Робертсон, Эдмунд Ф. (2000). «Индийские цифры» . MacTutor Архив истории математики . Университет Сент-Эндрюс .
- Смит, Дэвид Юджин ; Карпинский, Луи Шарль (1911). Индо-арабские цифры . Бостон: Джинн.
Дальнейшее чтение
[ редактировать ]- Меннингер, Карл В. (1969). Числовые слова и числовые символы: культурная история чисел . МТИ Пресс. ISBN 0-262-13040-8 .
- О генеалогии современных цифр Эдварда Клайва Бэйли
